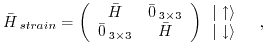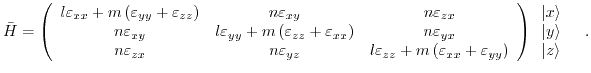Next: 3.5.2 The k.p Method
Up: 3.5 Strain and Bulk
Previous: 3.5 Strain and Bulk
Subsections
Bardeen and Shockley [165] originally developed the deformation potential theory. Herring and Vogt [166] generalized this theory. Bir and Pikus [161] studied various semiconductors via group theory and showed how to calculate strain effects on the band structure with deformation potentials. A short introduction into the deformation potential theory is given subsequently.
The deformation potential theory introduces an additional Hamiltonian
 , that is attributed to strain and its effects on the band structure. This Hamiltonian is based on first order perturbation theory and its matrix elements are defined by
, that is attributed to strain and its effects on the band structure. This Hamiltonian is based on first order perturbation theory and its matrix elements are defined by
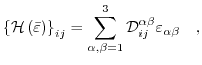 |
(3.15) |
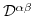 denotes the deformation potential operator which transforms under symmetry operations as second rank tensor [167] and
denotes the deformation potential operator which transforms under symmetry operations as second rank tensor [167] and
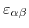 describes the
describes the
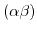 strain tensor component. The subscripts
strain tensor component. The subscripts
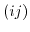 in
in
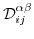 denote the matrix element of the operator
denote the matrix element of the operator
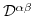 . Due to the symmetry of the strain tensor with respect to
. Due to the symmetry of the strain tensor with respect to 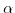 and
and 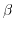 , also the deformation potential operator has to obey this symmetry
, also the deformation potential operator has to obey this symmetry
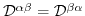 and thus limits the number of independent deformation potential operators to six.
and thus limits the number of independent deformation potential operators to six.
In the case of cubic semiconductors the edges of the conduction band and the valence band are located on symmetry lines. These symmetries are reproduced in the energy band structure and in the basis states. Furthermore, the symmetry of the basis states allows to describe the deformation potential operator of a particular band via two or three deformation potential constants [166].
Although, theoretically the deformation potential constants can be calculated via the empirical pseudo potential method or by ab initio methods, it is more convenient to fit the deformation potentials to experimental results obtained by electrical, optical, microwave techniques, or by analyzing stress induced absorption edges. Even though, theoretical predictions and measurements match quite well, deformation potentials in literature and found by different methods deviate from each other [168].
Cubic crystalls exhibit a strain induced energy shift for the non-degenerate energy levels of the conduction band. Along the 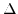 symmetry line it is sufficient to describe the deformation potential operators
symmetry line it is sufficient to describe the deformation potential operators
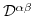 as scalars by one or two independent constants. The energy shifts of the conduction band edge of valleys along the
as scalars by one or two independent constants. The energy shifts of the conduction band edge of valleys along the
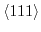 and
and
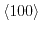 directions is determined by two independent deformation potential constants 3.1 [169]:
directions is determined by two independent deformation potential constants 3.1 [169]:
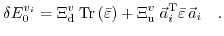 |
(3.16) |
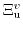 describes the uniaxial- and
describes the uniaxial- and
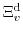 the dilatation deformation potential constants for valleys of the type
the dilatation deformation potential constants for valleys of the type
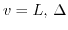 .
.
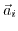 denotes the unit vector parallel to the
denotes the unit vector parallel to the 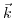 vector of valley
vector of valley  . The
. The
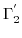 conduction band minimum valley shift can be determined from a single deformation potential constant
conduction band minimum valley shift can be determined from a single deformation potential constant
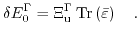 |
(3.17) |
Via the two relations from above the valley splitting from uniaxial stress along arbitrary directions can be calculated.
Additionally to strain induced energy shifts of energy levels of the conduction band edges, there can also be a partially or complete lifting of degeneracy for degenerate bands, caused by the reduction of symmetry. Due to the special symmetry of the diamond structure (three glide reflection planes at  ,
,  and
and 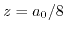 ), the lowest two conduction bands
), the lowest two conduction bands
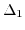 and
and
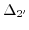 touch at the zone boundary
touch at the zone boundary  . Shear strain
. Shear strain
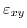 due to stress along
due to stress along
![$ \left[110\right]$](img403.png) reduces the symmetry of the diamond crystal structure and produces an orthorhombic crystal.
The glide reflection plane
reduces the symmetry of the diamond crystal structure and produces an orthorhombic crystal.
The glide reflection plane 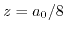 is removed by the shear strain component and thus the degeneracy of the two lowest conduction bands
is removed by the shear strain component and thus the degeneracy of the two lowest conduction bands
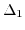 and
and
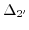 at the symmetry points
at the symmetry points
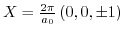 is lifted [161,170]. It should be mentioned that in biaxially strained
is lifted [161,170]. It should be mentioned that in biaxially strained 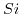 layers grown on
layers grown on
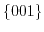
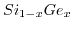 substrates and for uniaxially strained/stressed
substrates and for uniaxially strained/stressed 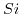 along a fourfold rotation axis
along a fourfold rotation axis
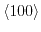 the glide reflection symmetry is preserved.
the glide reflection symmetry is preserved.
Bir and Pikus found from k.p theory, that when the degeneracy at the zone boundary  is lifted, a relatively large change in the energy dispersion of the conduction band minimum located close to this
is lifted, a relatively large change in the energy dispersion of the conduction band minimum located close to this  point arises [161]. This effect was experimentally proved for
point arises [161]. This effect was experimentally proved for 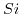 by Hensel and Hasegawa [170], who measured the change in effective mass for stress along
by Hensel and Hasegawa [170], who measured the change in effective mass for stress along
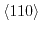 , and by Laude [171], who showed the effect via the indirect exciton spectrum.
, and by Laude [171], who showed the effect via the indirect exciton spectrum.
Therefore, in order to take the lifting of the degeneracy of the two lowest conduction bands
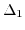 and
and
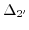 at the
at the  points
points
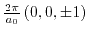 into account, (3.16) has to be adapted [170]
into account, (3.16) has to be adapted [170]
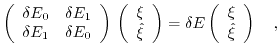 |
(3.18) |
where
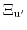 denotes a new deformation potential,
denotes a new deformation potential,
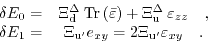 |
(3.19) |
The solutions of the eigenvalue problem look like:
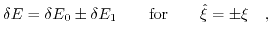 |
(3.20) |
which shows that at the  points
points
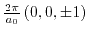 the band shifts by an amount of
the band shifts by an amount of
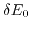 (like before in (3.16)) plus an additional splitting of
(like before in (3.16)) plus an additional splitting of
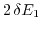 , which lifts the degeneracy. (3.19) shows the proportional dependence on shear strain
, which lifts the degeneracy. (3.19) shows the proportional dependence on shear strain
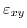 for the splitting
for the splitting
![$\displaystyle \left(E_{\Delta_{1}}- E_{\Delta_{2'}}\right) \Big\vert _{X_{\left[001\right]}}=2 \delta E_{1} = 4 \Xi_{\mathrm{u}'} \varepsilon_{xy} \quad.$](img416.png) |
(3.21) |
A value of
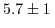 eV has been predicted by Hensel for the shear deformation potential
eV has been predicted by Hensel for the shear deformation potential
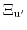 [170]. Laude [171] confirmed this value by his measurement of
[170]. Laude [171] confirmed this value by his measurement of
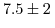 eV via the indirect exciton spectrum of
eV via the indirect exciton spectrum of 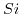 .
.
The splitting is already strongly pronounced for shear strain 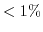 . Due to the lifting of the degeneracy the
. Due to the lifting of the degeneracy the
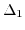 conduction band is deformed close to the symmetry points
conduction band is deformed close to the symmetry points
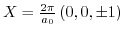 (Fig. 3.2).
(Fig. 3.2).
Figure 3.2:
Energy dispersion of the conduction bands
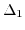 and
and
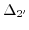 near the zone boundary
near the zone boundary  point along
point along
![$ \left [001\right ]$](img8.png) . For
. For
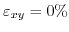 the conduction bands are degenerate at the zone boundary. Introduction of shear strain
the conduction bands are degenerate at the zone boundary. Introduction of shear strain
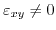 lifts this degeneracy and opens up a gap. The energy separation
lifts this degeneracy and opens up a gap. The energy separation
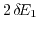 between the bands becomes larger with increasing strain
between the bands becomes larger with increasing strain
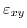 . At the same time the two minima of the lower conduction band
. At the same time the two minima of the lower conduction band
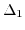 move closer to the zone boundary with rising strain
move closer to the zone boundary with rising strain
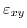 , until they merge at the zone boundary and stay there for further increasing strain.
, until they merge at the zone boundary and stay there for further increasing strain.
![\includegraphics[width=1.1\textwidth]{figures/energydispersion.ps}](img422.png) |
i
A non-vanishing shear strain component
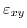 has the following effects on the energy dispersion of the lowest conduction band:
has the following effects on the energy dispersion of the lowest conduction band:
- The band edge energy of the valley pair along
![$ \left [001\right ]$](img8.png) direction shifts down with respect to the other four valleys along
direction shifts down with respect to the other four valleys along
![$ \left [100\right ]$](img18.png) and
and
![$ \left [010\right ]$](img19.png) .
.
- The effective mass of the valley pair along
![$ \left [001\right ]$](img8.png) changes with increasing
changes with increasing
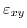 .
.
- The conduction band minima along
![$ \left [001\right ]$](img8.png) move to the zone boundary
move to the zone boundary  points at
points at
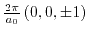 with increasing
with increasing
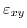 .
.
Figure:3.3
Energy dispersion of the two lowest conduction bands at the zone boundaries
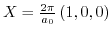 and
and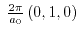 . The band separation of unstrained
. The band separation of unstrained 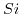 at the conduction band edge
at the conduction band edge
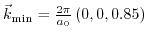 is denoted by
is denoted by 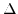 . Contrary to the conduction bands along
. Contrary to the conduction bands along
![$ \left [001\right ]$](img8.png) the conduction bands along
the conduction bands along
![$ \left [100\right ]$](img18.png) and
and
![$ \left [010\right ]$](img19.png) are not affected by shear strain
are not affected by shear strain
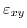 .
.
![\includegraphics[width=1.1\textwidth]{figures/energydispersion2.ps}](img425.png) |
For differing strains (
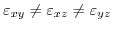 ), the conduction band minima along the
), the conduction band minima along the
 axes are different in their energies, causing a repopulation between the six conduction band valleys. This kind of effect is not covered with (3.16), due to the negligence of possible degeneracy liftings by shear strain and by ignoring a possible repopulation of energy states.
axes are different in their energies, causing a repopulation between the six conduction band valleys. This kind of effect is not covered with (3.16), due to the negligence of possible degeneracy liftings by shear strain and by ignoring a possible repopulation of energy states.
The model presented shows no change in the conduction bands near the zone boundaries
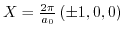 and
and
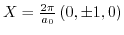 for a shear component
for a shear component
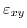 (Fig. 3.3). However, shear components like
(Fig. 3.3). However, shear components like
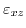 or
or
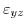 lift the degeneracy at
lift the degeneracy at
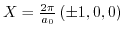 or
or
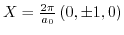 .
.
Applying a degenerate k.p theory at the zone boundary  point [161,170] enables an analytical description for the valley shift along the
point [161,170] enables an analytical description for the valley shift along the 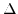 direction. Shear strain
direction. Shear strain
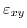 causes an energy shift between the conduction band valleys along
causes an energy shift between the conduction band valleys along
![$ \left [100\right ]$](img18.png) /
/
![$ \left [010\right ]$](img19.png) and the valleys along
and the valleys along
![$ \left [001\right ]$](img8.png) .
This shift is described by
.
This shift is described by
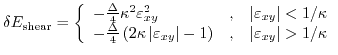 |
(3.22) |
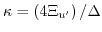 is a dimensionless parameter and
is a dimensionless parameter and 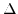 denotes the band separation between the lowest two conduction bands at the conduction band edge
denotes the band separation between the lowest two conduction bands at the conduction band edge
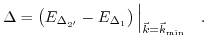 |
(3.23) |
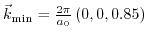 denotes the position of the band edge in the unstrained lattice.
denotes the position of the band edge in the unstrained lattice.
Caused by the degeneracy at the maximum of the valence bands the deformation potential is different than that of the conduction bands. The deformation potential operators
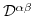 are no longer scalars and have to be expressed as
are no longer scalars and have to be expressed as 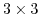 matrices. Using symmetries the six independent operators can be described via three independent entries, commonly named
matrices. Using symmetries the six independent operators can be described via three independent entries, commonly named 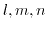 or
or 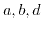 , related to the applied set of eigenfunctions [172].
For the basis
, related to the applied set of eigenfunctions [172].
For the basis
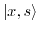 ,
,
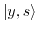 ,
,
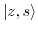 , with
, with
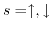 denoting the spin state, the perturbation Hamiltonian takes the following form:
denoting the spin state, the perturbation Hamiltonian takes the following form:
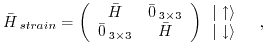 |
(3.24) |
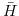 denotes the
denotes the 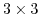 matrix
matrix
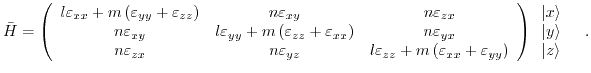 |
(3.25) |
In the case of the valence band the description of the strain induced shifts of the heavy-hole, light-hole, and the split-off band are more complex[169].
Footnotes
- ... constants3.1
- neglecting strain induced splitting of the degenerate conduction bands
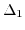 and
and
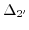 at the
at the  point
point




Next: 3.5.2 The k.p Method
Up: 3.5 Strain and Bulk
Previous: 3.5 Strain and Bulk
T. Windbacher: Engineering Gate Stacks for Field-Effect Transistors
![]() , that is attributed to strain and its effects on the band structure. This Hamiltonian is based on first order perturbation theory and its matrix elements are defined by
, that is attributed to strain and its effects on the band structure. This Hamiltonian is based on first order perturbation theory and its matrix elements are defined by
![]() describes the uniaxial- and
describes the uniaxial- and
![]() the dilatation deformation potential constants for valleys of the type
the dilatation deformation potential constants for valleys of the type
![]() .
.
![]() denotes the unit vector parallel to the
denotes the unit vector parallel to the ![]() vector of valley
vector of valley ![]() . The
. The
![]() conduction band minimum valley shift can be determined from a single deformation potential constant
conduction band minimum valley shift can be determined from a single deformation potential constant
![]() is lifted, a relatively large change in the energy dispersion of the conduction band minimum located close to this
is lifted, a relatively large change in the energy dispersion of the conduction band minimum located close to this ![]() point arises [161]. This effect was experimentally proved for
point arises [161]. This effect was experimentally proved for ![]() by Hensel and Hasegawa [170], who measured the change in effective mass for stress along
by Hensel and Hasegawa [170], who measured the change in effective mass for stress along
![]() , and by Laude [171], who showed the effect via the indirect exciton spectrum.
, and by Laude [171], who showed the effect via the indirect exciton spectrum.
![]() and
and
![]() at the
at the ![]() points
points
![]() into account, (3.16) has to be adapted [170]
into account, (3.16) has to be adapted [170]
![]() . Due to the lifting of the degeneracy the
. Due to the lifting of the degeneracy the
![]() conduction band is deformed close to the symmetry points
conduction band is deformed close to the symmetry points
![]() (Fig. 3.2).
(Fig. 3.2).
![\includegraphics[width=1.1\textwidth]{figures/energydispersion.ps}](img422.png)
![]() has the following effects on the energy dispersion of the lowest conduction band:
has the following effects on the energy dispersion of the lowest conduction band:
![\includegraphics[width=1.1\textwidth]{figures/energydispersion2.ps}](img425.png)
![]() ), the conduction band minima along the
), the conduction band minima along the
![]() axes are different in their energies, causing a repopulation between the six conduction band valleys. This kind of effect is not covered with (3.16), due to the negligence of possible degeneracy liftings by shear strain and by ignoring a possible repopulation of energy states.
axes are different in their energies, causing a repopulation between the six conduction band valleys. This kind of effect is not covered with (3.16), due to the negligence of possible degeneracy liftings by shear strain and by ignoring a possible repopulation of energy states.
![]() and
and
![]() for a shear component
for a shear component
![]() (Fig. 3.3). However, shear components like
(Fig. 3.3). However, shear components like
![]() or
or
![]() lift the degeneracy at
lift the degeneracy at
![]() or
or
![]() .
.
![]() point [161,170] enables an analytical description for the valley shift along the
point [161,170] enables an analytical description for the valley shift along the ![]() direction. Shear strain
direction. Shear strain
![]() causes an energy shift between the conduction band valleys along
causes an energy shift between the conduction band valleys along
![]() /
/
![]() and the valleys along
and the valleys along
![]() .
This shift is described by
.
This shift is described by
![]() denotes the position of the band edge in the unstrained lattice.
denotes the position of the band edge in the unstrained lattice.