



Next: 4. Quantum Confinement and
Up: 3.5 Strain and Bulk
Previous: 3.5.1 Deformation Potential Theory
Subsections
The k.p method allows to derive analytical expressions for the energy dispersion and the effective masses [161]. It enables the extrapolation of the band structure over the entire Brillouin zone from the energy gaps and matrix elements at the zone center. In addition to the common use of the k.p method to model the valence band of semiconductors, it is also well suited to describe the influence of strain on the conduction band minimum.
The k.p method can be derived from the one-electron Schrödinger equation as follows:
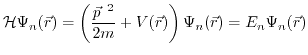 |
(3.26) |
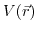 denotes the periodic lattice potential and
denotes the periodic lattice potential and
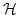 the one-electron Hamilton operator.
the one-electron Hamilton operator. 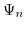 describes the one-electron wave function in an eigenstate
describes the one-electron wave function in an eigenstate 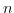 and
and 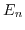 the eigenenergy for the eigenstate
the eigenenergy for the eigenstate 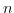 . Due to the periodicity of the lattice potential (3.26) the Bloch theorem is applicable and the solution can be written in the form of:
. Due to the periodicity of the lattice potential (3.26) the Bloch theorem is applicable and the solution can be written in the form of:
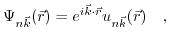 |
(3.27) |
The wave function
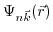 can be expressed as the product of a plane wave and the function
can be expressed as the product of a plane wave and the function
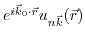 , which reflects the periodicity of the lattice.
, which reflects the periodicity of the lattice. 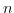 denotes the band index and
denotes the band index and 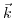 represents a wave vector. If the given potential
represents a wave vector. If the given potential
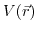 only depends on one spatial coordinate (also called local), (3.27) can be substituted in (3.26).
only depends on one spatial coordinate (also called local), (3.27) can be substituted in (3.26).
Luttinger [173] showed that it is possible to use the eigenfunctions of the ground states as a complete set of eigenfunctions and that the wave function can be expanded by
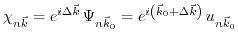 |
(3.28) |
for
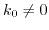 . Inserting (3.28) into (3.26) yields:
. Inserting (3.28) into (3.26) yields:
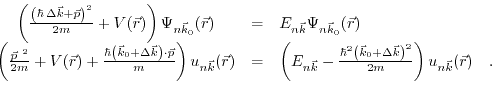 |
(3.29) |
This way, for any fixed wave vector
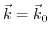 , (3.29) for the unperturbed system, delivers a complete set of eigenfunctions
, (3.29) for the unperturbed system, delivers a complete set of eigenfunctions
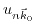 , which completely cover the space of the lattice periodic functions in real space. Therefore, the wave function
, which completely cover the space of the lattice periodic functions in real space. Therefore, the wave function
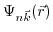 at
at 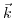 , for the full system, can be expressed via
, for the full system, can be expressed via
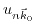
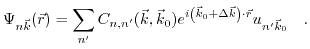 |
(3.30) |
As soon as the eigenenergy
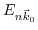 and the
and the
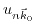 of the unperturbed system are determined, the eigenfunctions
of the unperturbed system are determined, the eigenfunctions
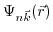 and eigenenergies
and eigenenergies
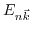 can be calculated for any
can be calculated for any
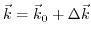 in the vicinity of
in the vicinity of
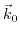 by accounting the
by accounting the
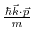 term in (3.29) as a perturbation. This method has been introduced by Seitz [174] and extended by [172,173,175] to study the band structure of semiconductors.
term in (3.29) as a perturbation. This method has been introduced by Seitz [174] and extended by [172,173,175] to study the band structure of semiconductors.
Due to the
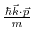 term in (3.29) this method is also known as the k.p method. Provided that the energies at
term in (3.29) this method is also known as the k.p method. Provided that the energies at
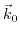 and that the matrix elements of
and that the matrix elements of 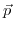 between the wave functions, or the wave functions themselves, are known, the band structure for small
between the wave functions, or the wave functions themselves, are known, the band structure for small
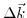 's around
's around
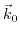 can be calculated. The entire first Brillouin zone can be calculated by diagonalizing (3.29) numerically, provided a sufficiently large set of
can be calculated. The entire first Brillouin zone can be calculated by diagonalizing (3.29) numerically, provided a sufficiently large set of
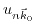 to approximate the complete set of basis functions is used [172].
to approximate the complete set of basis functions is used [172].
The following subsections will explain the effective masses for the non-degenerate conduction band of silicon and the energy dispersion utilizing a non-degenerate k.p theory. In order to analyze the effects of shear strain on the two lowest conduction bands
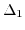 and
and
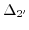 , the k.p method is adapted to enable degeneracy, due to the coincidence of the
, the k.p method is adapted to enable degeneracy, due to the coincidence of the
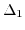 and
and
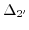 bands at the
bands at the  point.
point.
The conduction band minima of silicon reside on the
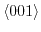 axes at a distance of
axes at a distance of
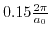 from the
from the  symmetry points. By means of non-degenerate perturbation theory and the knowledge of the eigenenergies
symmetry points. By means of non-degenerate perturbation theory and the knowledge of the eigenenergies
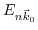 and the wave functions
and the wave functions
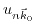 at the conduction band minima
at the conduction band minima
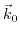 , the eigenvalues
, the eigenvalues
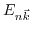 at neighboring points
at neighboring points 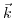 can be expanded to second order terms in
can be expanded to second order terms in 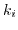 .
.
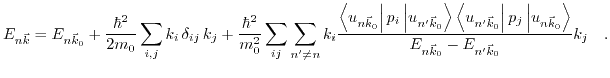 |
(3.31) |
Scalar products
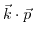 are expressed via index notation
are expressed via index notation
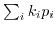 and the matrix elements with Dirac's notation
and the matrix elements with Dirac's notation
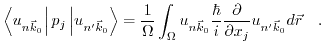 |
(3.32) |
The linear terms in 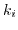 can be set to zero under the assumption that
can be set to zero under the assumption that
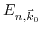 is a minimum. The expression for the effective mass tensor
is a minimum. The expression for the effective mass tensor
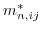 can be derived from the dispersion relation (3.31)
can be derived from the dispersion relation (3.31)
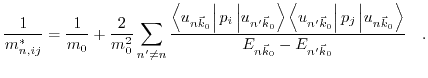 |
(3.33) |
The effective mass tensor for the lowest conduction band
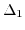 in diamond crystal structures is characterized by two masses. In the principal coordinate system for the
in diamond crystal structures is characterized by two masses. In the principal coordinate system for the
![$ \left [001\right ]$](img8.png) valley the effective masses can be written as
valley the effective masses can be written as
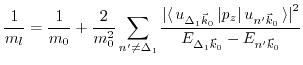 |
(3.34) |
and
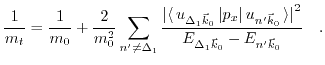 |
(3.35) |
 denotes the band index
denotes the band index  of the lowest conduction band. Therefore, the energy dispersion can be formulated as:
of the lowest conduction band. Therefore, the energy dispersion can be formulated as:
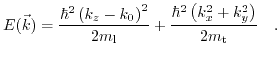 |
(3.36) |
From the derived equations follows that due to the coupling between electronic states in different bands (via k.p term), an electron in a solid has a different mass than a free electron. The coupling terms are related to the following criteria:
- The bigger the energetic gap between two bands, the smaller is the effect on the effective mass. The relative importance of a band
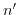 to the effective mass of band
to the effective mass of band 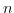 is controlled by the energy gap between the two bands.
is controlled by the energy gap between the two bands.
- All bands
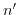 with non-zero matrix elements
with non-zero matrix elements
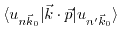 can be found via the matrix element theorem [176] by group theoretical considerations checking all possible symmetries for
can be found via the matrix element theorem [176] by group theoretical considerations checking all possible symmetries for
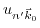 .
.
It is possible to calculate numerically all matrix elements and subsequently the effective masses from (3.33) via the empirical pseudo potential method [177].
(3.55) only requires the direction of the 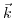 vector, indicating the location of the valley, to describe the shift of the valley minima. Hence, the valley shift is independent of the exact value of the wave vector
vector, indicating the location of the valley, to describe the shift of the valley minima. Hence, the valley shift is independent of the exact value of the wave vector 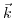 and all
and all 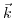 points belonging to a particular valley experience the same shift. Since the effective mass is given by the second derivative of the energy dispersion
points belonging to a particular valley experience the same shift. Since the effective mass is given by the second derivative of the energy dispersion
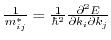 and (3.16) does not change the curvature of the energy band, the formula predicts no change in the effective electron mass due to strain.
and (3.16) does not change the curvature of the energy band, the formula predicts no change in the effective electron mass due to strain.
However, there is a clear experimental proof that shear strain changes the effective masses of electrons in the lowest conduction band[170] and the exciton spectrum of silicon[171]. In order to explain this behavior one has to take the splitting of the lowest two conduction bands at the  symmetry point by shear strain into account. The lifting of the degeneracy can be calculated with the deformation potential constant
symmetry point by shear strain into account. The lifting of the degeneracy can be calculated with the deformation potential constant 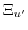 via (3.20). (3.20) is only valid at the
via (3.20). (3.20) is only valid at the  symmetry point and cannot be used to predict the effect of strain on the valley minima
symmetry point and cannot be used to predict the effect of strain on the valley minima
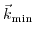 . In order to circumvent this obstacle a degenerate k.p theory has to be applied around the
. In order to circumvent this obstacle a degenerate k.p theory has to be applied around the  symmetry point.
symmetry point.
A different approach was adapted in [161]. The Hamiltonian at the
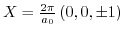 points can be described via the theory of invariants:
points can be described via the theory of invariants:
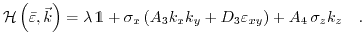 |
(3.37) |
where,
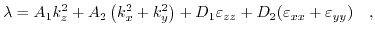 |
(3.38) |
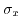 and
and
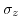 are the Pauli's matrices and
are the Pauli's matrices and 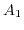 and
and 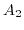 denote scalar constants
denote scalar constants
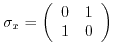 and and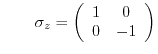 |
(3.39) |
The scalar constants 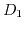 ,
, 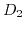 , and
, and 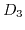 are connected to the deformation potential constants
are connected to the deformation potential constants 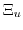 ,
, 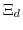 , and
, and 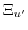 through
through
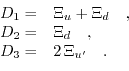 |
(3.40) |
From (3.37) eigenvalues can be calculated which represent the energy dispersion for the first and second conduction band
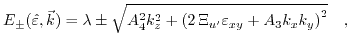 |
(3.41) |
where 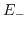 denotes the energy dispersion of
denotes the energy dispersion of
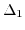 and
and 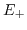 that of
that of
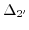 .
Under the assumption that this description is valid around the
.
Under the assumption that this description is valid around the  point up to the minimum of the lowest conduction band at
point up to the minimum of the lowest conduction band at
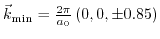 ,
, 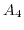 and
and 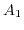 can be related to each other via
can be related to each other via
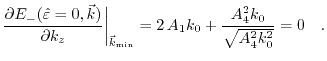 |
(3.42) |
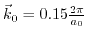 describes the distance of the conduction band minimum of unstrained silicon to the
describes the distance of the conduction band minimum of unstrained silicon to the  point.
point. 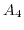 can be determined from (3.42)
can be determined from (3.42)
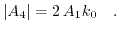 |
(3.43) |
The effect of shear strain on the shape of the lowest conduction band is examined in the following section.
Up to now it has been assumed that the conduction band minima are located at
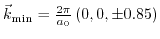 . This is only valid for small shear strain.
The minimum of the conduction band moves towards the
. This is only valid for small shear strain.
The minimum of the conduction band moves towards the  point in conjunction with an increasing splitting between the conduction bands, when the shear strain rises (as can be seen in Fig. 3.2). This causes a change in the shape of the conduction bands and the assumption that the minima lie fixed at
point in conjunction with an increasing splitting between the conduction bands, when the shear strain rises (as can be seen in Fig. 3.2). This causes a change in the shape of the conduction bands and the assumption that the minima lie fixed at
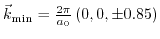 does not hold anymore.
does not hold anymore.
Therefore, a model which is able to cover the effects of shear strain on the effective masses has to take the movement of the conduction band as a function of strain into account. In the following a model will be derived that takes this movement of
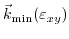 into account.
into account.
Starting with (3.41) and setting
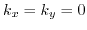 the minimum can be found from the dispersion relation
the minimum can be found from the dispersion relation
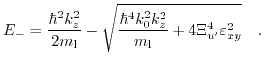 |
(3.44) |
The constants 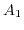 and
and 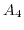 are replaced with the relations (3.43) and (3.36), and
are replaced with the relations (3.43) and (3.36), and
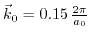 describes the position of the conduction band minimum measured from the zone boundary
describes the position of the conduction band minimum measured from the zone boundary  . Setting the first derivative of (3.44) to zero,
. Setting the first derivative of (3.44) to zero,
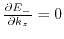 , and solving for
, and solving for 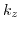 results in the desired relation between
results in the desired relation between
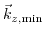 and shear strain.
and shear strain.
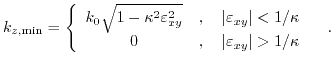 |
(3.45) |
Here
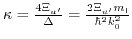 is introduced and represents the ratio between the shear deformation potential
is introduced and represents the ratio between the shear deformation potential 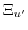 and the band separation between the two lowest conduction bands
and the band separation between the two lowest conduction bands 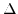 at zero shear strain (Fig. 3.3).
(3.45) shows that for strain smaller than
at zero shear strain (Fig. 3.3).
(3.45) shows that for strain smaller than 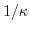 , the minimum position shifts towards the
, the minimum position shifts towards the  point. At
point. At
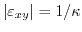 , the minimum is located at the
, the minimum is located at the  point (
point (
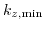 ). Increasing shear strain above
). Increasing shear strain above
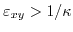 does not shift
does not shift
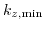 anymore. The change of shape of the two lowest conduction bands
anymore. The change of shape of the two lowest conduction bands
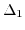 and
and
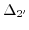 and accordingly the position change of the minimum with increasing shear strain can be seen in Fig. 3.2.
and accordingly the position change of the minimum with increasing shear strain can be seen in Fig. 3.2.
The strain dependent longitudinal mass
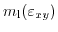 can be calculated from (3.44) with
can be calculated from (3.44) with
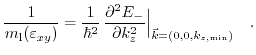 |
(3.46) |
After some algebraic manipulations the strain dependent mass
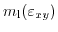 can be expressed as
can be expressed as
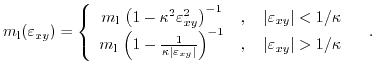 |
(3.47) |
Accordingly to (3.45) the dependence of the longitudinal masses is different for a strain level above or below 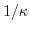 .
For the derivation of the transversal masses we rotate the principal coordinate system by
.
For the derivation of the transversal masses we rotate the principal coordinate system by
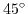 around the z-axis with the following transformation:
around the z-axis with the following transformation:
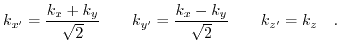 |
(3.48) |
The energy dispersion in the rotated coordinate system is
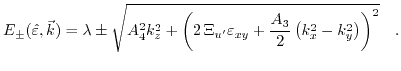 |
(3.49) |
The effective mass in the
![$ \left[110\right]$](img403.png) and
and
![$ \left[ 1\bar{1}0\right]$](img522.png) directions is defined by
directions is defined by
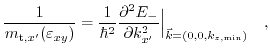 |
(3.50) |
and
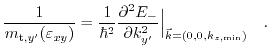 |
(3.51) |
Applying (3.50) and (3.51) to (3.49) gives for the
![$ \left[110\right]$](img403.png) direction
direction
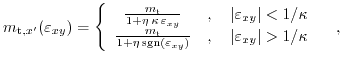 |
(3.52) |
and
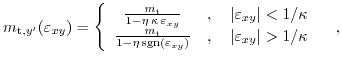 |
(3.53) |
for the
![$ \left[ 1\bar{1}0\right]$](img522.png) direction with the parameter
direction with the parameter
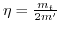 and
and 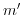 is defined by
is defined by
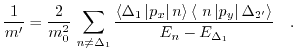 |
(3.54) |
As can be seen along the
![$ \left[110\right]$](img403.png) direction the effective mass is reduced (mobility is enhanced) for
direction the effective mass is reduced (mobility is enhanced) for
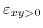 , while for the
, while for the
![$ \left[ 1\bar{1}0\right]$](img522.png) direction the effective mass is increased (the mobility is reduced) for increasing shear strain (
direction the effective mass is increased (the mobility is reduced) for increasing shear strain (
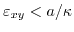 ). For shear strain above
). For shear strain above
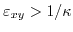 the effective mass is a constant which depends on the sign of the strain.
the effective mass is a constant which depends on the sign of the strain.
The analytical valley shift induced by shear strain
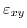 (given in (3.22)) can now be calculated. Substituting the expression for
(given in (3.22)) can now be calculated. Substituting the expression for
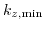 from (3.45) into equation (3.44) delivers the equation for shear strain.The shift between the valley pair along
from (3.45) into equation (3.44) delivers the equation for shear strain.The shift between the valley pair along
![$ \left [001\right ]$](img8.png) and the valley pairs
and the valley pairs
![$ \left [100\right ]$](img18.png) or
or
![$ \left [010\right ]$](img19.png) due to
due to
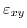 can be obtained in the form of
can be obtained in the form of
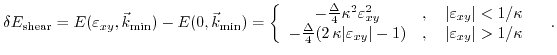 |
(3.55) |




Next: 4. Quantum Confinement and
Up: 3.5 Strain and Bulk
Previous: 3.5.1 Deformation Potential Theory
T. Windbacher: Engineering Gate Stacks for Field-Effect Transistors
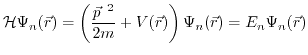
![]() can be expressed as the product of a plane wave and the function
can be expressed as the product of a plane wave and the function
![]() , which reflects the periodicity of the lattice.
, which reflects the periodicity of the lattice. ![]() denotes the band index and
denotes the band index and ![]() represents a wave vector. If the given potential
represents a wave vector. If the given potential
![]() only depends on one spatial coordinate (also called local), (3.27) can be substituted in (3.26).
only depends on one spatial coordinate (also called local), (3.27) can be substituted in (3.26).
![]() , (3.29) for the unperturbed system, delivers a complete set of eigenfunctions
, (3.29) for the unperturbed system, delivers a complete set of eigenfunctions
![]() , which completely cover the space of the lattice periodic functions in real space. Therefore, the wave function
, which completely cover the space of the lattice periodic functions in real space. Therefore, the wave function
![]() at
at ![]() , for the full system, can be expressed via
, for the full system, can be expressed via
![]()
![]() term in (3.29) this method is also known as the k.p method. Provided that the energies at
term in (3.29) this method is also known as the k.p method. Provided that the energies at
![]() and that the matrix elements of
and that the matrix elements of ![]() between the wave functions, or the wave functions themselves, are known, the band structure for small
between the wave functions, or the wave functions themselves, are known, the band structure for small
![]() 's around
's around
![]() can be calculated. The entire first Brillouin zone can be calculated by diagonalizing (3.29) numerically, provided a sufficiently large set of
can be calculated. The entire first Brillouin zone can be calculated by diagonalizing (3.29) numerically, provided a sufficiently large set of
![]() to approximate the complete set of basis functions is used [172].
to approximate the complete set of basis functions is used [172].
![]() and
and
![]() , the k.p method is adapted to enable degeneracy, due to the coincidence of the
, the k.p method is adapted to enable degeneracy, due to the coincidence of the
![]() and
and
![]() bands at the
bands at the ![]() point.
point.
![]() axes at a distance of
axes at a distance of
![]() from the
from the ![]() symmetry points. By means of non-degenerate perturbation theory and the knowledge of the eigenenergies
symmetry points. By means of non-degenerate perturbation theory and the knowledge of the eigenenergies
![]() and the wave functions
and the wave functions
![]() at the conduction band minima
at the conduction band minima
![]() , the eigenvalues
, the eigenvalues
![]() at neighboring points
at neighboring points ![]() can be expanded to second order terms in
can be expanded to second order terms in ![]() .
.
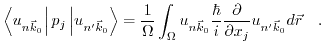
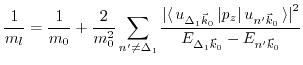
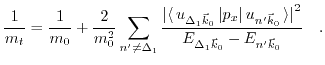
![]() symmetry point by shear strain into account. The lifting of the degeneracy can be calculated with the deformation potential constant
symmetry point by shear strain into account. The lifting of the degeneracy can be calculated with the deformation potential constant ![]() via (3.20). (3.20) is only valid at the
via (3.20). (3.20) is only valid at the ![]() symmetry point and cannot be used to predict the effect of strain on the valley minima
symmetry point and cannot be used to predict the effect of strain on the valley minima
![]() . In order to circumvent this obstacle a degenerate k.p theory has to be applied around the
. In order to circumvent this obstacle a degenerate k.p theory has to be applied around the ![]() symmetry point.
symmetry point.
![]() points can be described via the theory of invariants:
points can be described via the theory of invariants: 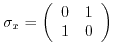 and
and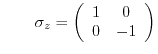
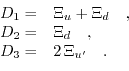
![]() . This is only valid for small shear strain.
The minimum of the conduction band moves towards the
. This is only valid for small shear strain.
The minimum of the conduction band moves towards the ![]() point in conjunction with an increasing splitting between the conduction bands, when the shear strain rises (as can be seen in Fig. 3.2). This causes a change in the shape of the conduction bands and the assumption that the minima lie fixed at
point in conjunction with an increasing splitting between the conduction bands, when the shear strain rises (as can be seen in Fig. 3.2). This causes a change in the shape of the conduction bands and the assumption that the minima lie fixed at
![]() does not hold anymore.
does not hold anymore.
![]() into account.
into account.
![]() the minimum can be found from the dispersion relation
the minimum can be found from the dispersion relation
![]() can be calculated from (3.44) with
can be calculated from (3.44) with
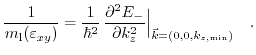
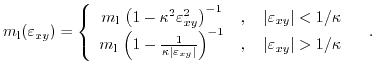
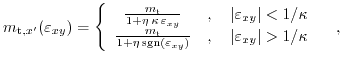
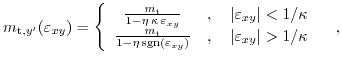
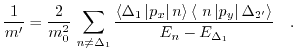
![]() direction the effective mass is reduced (mobility is enhanced) for
direction the effective mass is reduced (mobility is enhanced) for
![]() , while for the
, while for the
![]() direction the effective mass is increased (the mobility is reduced) for increasing shear strain (
direction the effective mass is increased (the mobility is reduced) for increasing shear strain (
![]() ). For shear strain above
). For shear strain above
![]() the effective mass is a constant which depends on the sign of the strain.
the effective mass is a constant which depends on the sign of the strain.
![]() (given in (3.22)) can now be calculated. Substituting the expression for
(given in (3.22)) can now be calculated. Substituting the expression for
![]() from (3.45) into equation (3.44) delivers the equation for shear strain.The shift between the valley pair along
from (3.45) into equation (3.44) delivers the equation for shear strain.The shift between the valley pair along
![]() and the valley pairs
and the valley pairs
![]() or
or
![]() due to
due to
![]() can be obtained in the form of
can be obtained in the form of