5.1 Electrochemistry of Ionic Soultions

Chemical and biological experiments are commonly carried out in ionic solutions [189]. The reason is that within polar solutions (e.g. water) the solvent molecules exhibit a non-vanishing dipole moment. This feature enables the reduction of the electric field between ionic bonds and allows to break up the initially strong ionic connections, leading to more chemically active reactants. Fig. 5.1 shows an example for a general structure of an ionic solution. It depicts a so called 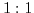$1:1$ solution [190], which implies that the valences' absolute value of the anion (negative ion) and the kation (positive ion) are equal. 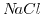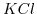$N\!aCl$and $K Cl$are two examples for a 1:1 solution/salt. The dissolved particles try to minimize the total energy of the system. This is accomplished by minimizing the repulsive forces between ions of equal charges. Thus, without external forces the charges are equally distributed across the electrolyte. Each ion is surrounded by an aggregate of water molecules. The charge of a water molecule is not symmetrically distributed, which causes a finite dipole moment. Therefore water is a polar solvent, and the polarity of water molecules enables it to dissolve ionic compounds by reducing the binding electric field between ions. The water shell around an ion changes the permittivity in it's vicinity and renders it less prone to electric fields originating from other ions. In this manner, the ions are free to move in the solvent, giving rise to a possible conduction path for an electrical current.

Not only the salt ions are dissolved in the solute but also the water molecules themselves can dissociate into ionic components. This is governed by the following chemical reaction [5]:

Figure 5.1: Most biological and chemical experiments are carried out in an ionic solution. Polar solutions (like water) can break up strong ionic bonds and ease chemical reactions. Each ion (red and dark blue) is surrounded by an aggregate of water molecules. The non-vanishing dipole moment of the water molecules weakens the electric field binding the ions together.

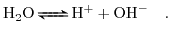$$\mathrm{H}_{\mathrm{2}}\mathrm{O} \autorightleftharpoons{}{} \mathrm{H}^{+} + \mathrm{OH}^{-}\quad.$$ (5.1)

Assuming that the reaction (5.1) is reversible and in equilibrium the law of mass action can be applied,

$$K_{\mathrm{eq}}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{H}_{2}\mathrm{O}\right]}\quad.$$ (5.2)

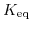$K_{\mathrm{eq}}$ denotes the equilibrium constant, $\left[H^{+}\right]$ the hydrogen concentration, $\left[\mathrm{OH}^{-}\right]$ the hydroxyl concentration, and $\left[\mathrm{H}_{\mathrm{2}}\mathrm{O}\right]$ the water concentration, respectively. Further, taking the density of water as constant ( 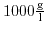$1000\frac{\mathrm{g}}{\mathrm{l}}$) the dependence of the ion concentrations on the equilibrium constants can be expressed directly:

$$K_{\mathrm{eq}}=\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{OH... ...\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right]}{55.56\mathrm{M}}\quad.$$ (5.3)

In this way we can define the dissociation constant of water as follows:

$$K_{\mathrm{w}}=55.56\mathrm{M}\cdot K_{\mathrm{eq}}= 1\cdot 10^{-14}=\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right]\quad.$$ (5.4)

The dissociation constant of water 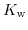$K_{\mathrm{w}}$ has a value of 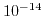$10^{-14}$ at room temperature. Due to the large range for hydrogen and hydroxyl concentrations it is convenient to reformulate (5.4) to a logarithmic scale:

$$\log_{10}(\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right])=p\mathrm{H}+p\mathrm{OH}=14\quad.$$ (5.5)

From (5.5) the widely in chemistry as a measure for the acidity of a solution used definition

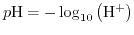$$p\mathrm{H}= - \log_{10}\left(\mathrm{H}^{+}\right)$$ (5.6)

can be deduced. This is definition complies with the acid definition by Arrhenius, as a substance that increases the concentraion of hydrogen ions. In Section 5.6 the influence of the hydrogen concentration on the operation of Ion-Sensitive Field-Effect Transistor (ISFET) devices will be enlightened by the site-binding model.