5.3 Insulator Surface Charge: The Double Layer

As mentioned in the Section 5.2.2, either by an externally applied voltage or by the equillibrium potential, charges gather at the electrode and in the surface area of electrolyte. The plentitude of charge carriers in the electrode lead to mutual repulsion and therefore all charge carriers will reside on the electrode surface. On the other hand, in the electrolyte the charge carriers are ions and these posses a larger radius compared to the charge carriers in the electrode (e.g. electrons in a metal). Therefore, a single layer of ions will not be able to compensate the surface charge of the electrode and a diffusive region of ions will form in the vicinity of the electrode surface. Due to the finite width of charges an electrostatic potential drop will arise in the diffusive layer. Combining concepts from electrostatic and statistical mechanics the diffusive layer can be described via the Poisson-Boltzmann equation. The diffusive layer is also known as Gouy-Chapman layer or electric double layer (depicted in Fig. 5.2). An extensive description of the Poisson-Boltzmann equation will be given in Section 6.2.1. Here, we will concentrate on the one-dimensional formulation for a 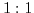$1:1$ electrolyte:

$$\frac{d^{2}\psi}{dx^{2}}=-\frac{1000\,q\,n_{A} }{\varepsilon_{0} ... ...silon_{\mathrm{sol}} } \left(\left[c^{+}\right]-\left[c^{-}\right]\right)\quad.$$ (5.11)

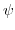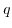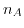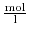$\psi$ denotes the electrostatic potential, $q$ the elementary charge, $n_{A}$ Avrogado's constant, and $\left[c^{+}\right],\left[c^{-}\right]$ the charge distributions for the positive and negative ions, in $\frac{\mathrm{mol}}{\mathrm{l}}$ respectively. Assuming positive and negative ions in thermodynamical equilibrium with their neighborhood, their ionic densities can be related to the electrostatic potential by the following Boltzmann distributions:

$$\begin{array}{ccc} \left[c^{+}\right]&=&c_{0}\,e^{-\frac{q \p... ...t]&=&c_{0}\,e^{\frac{q \psi}{k_{\text{B}} T}}\quad. \end{array}$$ (5.12)

Joining (5.11) and (5.12) leads to the Poisson-Boltzmann equation for a 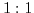$1:1$ electrolyte:

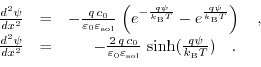$$\begin{array}{ccc} \frac{d^{2}\psi}{dx^{2}}&=&-\frac{q\,c_{0}... ...{sol}}}\,\sinh(\frac{q \psi}{k_{\text{B}} T})\quad. \end{array}$$ (5.13)

This ordinary non linear second order differential equation can only be solved analytically for very few cases and has to be treated with numerical methods.

The total charge density in the Gouy-Chapman layer can be calculated by ([192], derived in the Appendix C.):

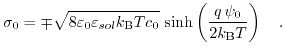$$\sigma_{0}=\mp\sqrt{8 \varepsilon_{0} \varepsilon_{sol} k_{\text{B}} Tc_{0}}\, \sinh\left(\frac{q\,\psi_{0}}{2k_{\text{B}} T}\right)\quad.$$ (5.14)