Next: 6.2.2 Poisson-Boltzmann Model with
Up: 6.2 Modeling BioFETs
Previous: 6.2 Modeling BioFETs
6.2.1 Poisson-Boltzmann Model
The often employed Poisson-Boltzmann model is a good approximation for electrolytes from several
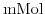 upwards. Assuming that the dissolved buffer ions are in thermodynamical equilibrium with their environment and their concentration only depends on the local potential, the charge contribution from the buffer can be written as sum over all ionic species of the buffer weighted with Boltzmann type terms
upwards. Assuming that the dissolved buffer ions are in thermodynamical equilibrium with their environment and their concentration only depends on the local potential, the charge contribution from the buffer can be written as sum over all ionic species of the buffer weighted with Boltzmann type terms
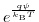 and their valences.
The Poisson-Boltzmann model has been already introduced in Section 5.3 and is now generalized to a two-dimensional formulation6.1:
and their valences.
The Poisson-Boltzmann model has been already introduced in Section 5.3 and is now generalized to a two-dimensional formulation6.1:
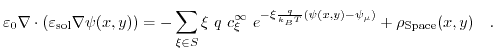 |
(6.1) |
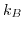 denotes Boltzmann's constant,
denotes Boltzmann's constant, 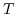 the temperature in Kelvin, and
the temperature in Kelvin, and 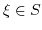 , where S contains the valences of the ions in the electrolyte.
, where S contains the valences of the ions in the electrolyte.
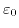 is the permittivity of vacuum, and
is the permittivity of vacuum, and 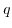 denotes the elementary charge.
denotes the elementary charge.
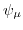 is the chemical potential.
is the chemical potential.
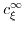 is the ion concentration in equilibrium, while
is the ion concentration in equilibrium, while
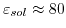 is the relative permittivity of water.
is the relative permittivity of water.
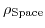 represents the average space charge density in the simulation zone, where the charged macromolecules are held.
represents the average space charge density in the simulation zone, where the charged macromolecules are held.
Footnotes
- ... formulation6.1
- In general this formulation can be extended to three dimensions, but due to the device geometry two-dimensional cuts are sufficient.




Next: 6.2.2 Poisson-Boltzmann Model with
Up: 6.2 Modeling BioFETs
Previous: 6.2 Modeling BioFETs
T. Windbacher: Engineering Gate Stacks for Field-Effect Transistors