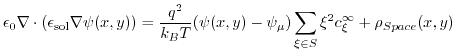6.2.5 Debye-Hückel Model

The Poisson-Boltzmann equation constitutes a nonlinear differential equation for the electrostatic potential. Frequently one is interested in a formulation which is numericaly less demanding or even an analytical solution. This has been done by Debye and Hückel [226] in 1923, who derived a linearized version of the Poisson-Boltzmann equation. Starting with the corresponding thermodynamical potential, they rigorously deduced the Poisson-Boltzmann model and from this their Debye-Hückel equation by Taylor expansion of the exponential terms, neglecting contributions higher than first order. This model is valid only for small potentials in relatively dilute electrolytes:

$$\epsilon_{0} \nabla \cdot (\epsilon_{\mathrm{sol}} \nabla \psi(x,... ...i(x,y)-\psi_{\mu})\sum_{\xi \in S} \xi^{2} c_{\xi}^{\infty} + \rho_{Space}(x,y)$$ (6.6)

From (6.6) two important properties can be gained. Firstly, the Debye length $\lambda _{\mathrm {D}}$:

$$\begin{array}{ccl} \lambda_{\mathrm{D}}&=&\sqrt{\frac{k_{\tex... ...athrm{sol}}}{2\,q^{2} I\left(\vec{x}\right)}}\quad. \end{array}$$ (6.7)

The Debye length $\lambda _{\mathrm {D}}$ is the characteristic length of the electrolytic system. It is the length at which the charge density and also the electric potential of an ion atmosphere reduces to $1/e$.

Figure 6.3: The dependence of the Debye length on ion concentration for a $1:1$ electrolytic solution. Higher salt concentration reduces the repulsion between complementary DNA strands, and thus accelerates the hybridization events, but, at the same time, decreases the Debye length $\lambda _{\mathrm {D}}$ and therefore the device signal.

The Debye length $\lambda _{\mathrm {D}}$ is also an important parameter in the sense of giving a rule of thumb on how far a charged macromolecule can be away from the dielectric-electrolyte interface without being completely shielded by the ions in the electrolyte. It is also a measure of how much of the macromolecule's charge is actually able to couple to the semiconductor without being screened for very large macromolecules (e.g. DNA). The Debye length $\lambda _{\mathrm {D}}$ affects the double layer thickness. Increasing the concentration or valence of the counterions compresses the double layer and raises the potential gradient.

The second parameter is already introduced in (6.8) and describes the ionic strength of the electrolyte defined as:

$$I(\vec{x})=\frac{1}{2}\,\sum_{\xi \in S} \xi^{2} c_{\xi}^{\infty}(\vec{x})$$ (6.8)

The ionic strength of a solution is a measure of the concentration of ions in the solution. The ionic compounds (e.g salts), dissociate into ions, when they are dissolved in water. Ionic strength is one of the main characteristics of a solution with dissolved ions, which influences many important properties like, the dissociation or solubility of different salts and the double layer thickness. The ionic strength is utilized to describe the strong deviations from the ideality typically experienced in ionic solutions via the Debye-Hückel theory. It is furthermore related to electrokinetic phenomena, electroacoustic phenomena in colloids and other heterogeneous systems and linked to the electric double layer (eq. (6.8)). The Debye length $\lambda _{\mathrm {D}}$ is inversely proportional to the square root of the ionic strength Fig. 6.3.

In order to minimize changes during a titration^6.2 in the activity quotient of solutes at lower concentrations, media with high ionic strength are employed. Natural waters such as seawater have a non-zero ionic strength due to the presence of dissolved salts which significantly affects their properties.

Footnotes

... titration^6.2

Titration is an often employed laboratory method of quantitative chemical analysis, used to determine the unknown concentration of a known reactant.