2.3.3.5 Six Moments Transport Model - Closure at 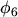
Taking the first six moments, eqns. (2.99) to
(2.104), into account give three balance and three flux equations
By using just a MAXWELL distribution function to close the system one would not obtain any
additional information as compared to the energy transport model. A shifted MAXWELL distribution function has only three independent parameters, namely its amplitude,
the displacement, and the standard deviation, which correspond to the carrier concentration
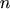 , the carrier velocity
, the carrier velocity 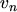 , and the carrier temperature
, and the carrier temperature 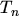 , respectively. By simply
increasing the number of considered moments of the distribution function no additional independent
variables can be found.
, respectively. By simply
increasing the number of considered moments of the distribution function no additional independent
variables can be found.
In analogy to statistical mathematics a quantity 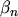 called kurtosis has been
introduced, which is in this work defined as the deviation of the fourth moment of the
non-MAXWELL distribution function from the fourth moment of a MAXWELL distribution function with the
same standard deviation
called kurtosis has been
introduced, which is in this work defined as the deviation of the fourth moment of the
non-MAXWELL distribution function from the fourth moment of a MAXWELL distribution function with the
same standard deviation
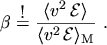 |
(2.174) |
The system is now closed at
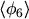 . Eqn. (2.126) is one
possible closure relation obtained from a MAXWELL distribution function. Other empirical
closures are also possible (eqn. (2.176)). By introducing an additional
temperature
. Eqn. (2.126) is one
possible closure relation obtained from a MAXWELL distribution function. Other empirical
closures are also possible (eqn. (2.176)). By introducing an additional
temperature 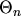 2.11
2.11
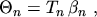 |
(2.175) |
the third power of the temperature 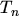 in eqn. (2.126) is substituted by
empirically combining different powers of
in eqn. (2.126) is substituted by
empirically combining different powers of 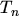 and
and 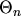
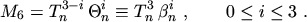 |
(2.176) |
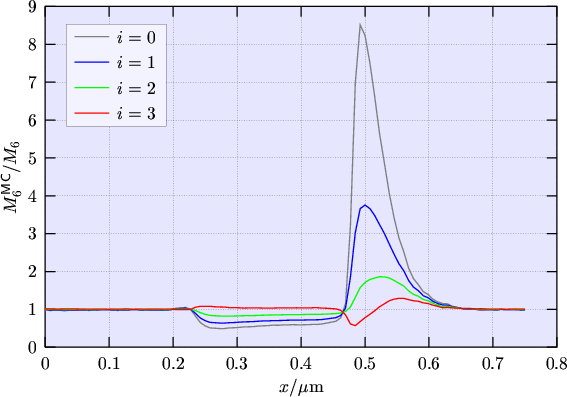
Simulations have shown, that the combination with 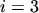 fits best to Monte Carlo data
[39, G5]. This is depicted in Fig. 2.4 where the different closure
relations are compared with the sixth moment obtained from a Monte Carlo simulation of a
one-dimensional
fits best to Monte Carlo data
[39, G5]. This is depicted in Fig. 2.4 where the different closure
relations are compared with the sixth moment obtained from a Monte Carlo simulation of a
one-dimensional 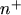 -
-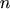 -
-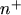 test structure. As can be seen, the closure for the case
test structure. As can be seen, the closure for the case 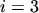 gives the smallest error within the channel. The convergence behavior of the resulting
discretized equation system also appeared most stable when using
gives the smallest error within the channel. The convergence behavior of the resulting
discretized equation system also appeared most stable when using 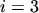 . Especially for
. Especially for 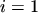 , which corresponds to closing the system with a MAXWELLian distribution function
eqn. (2.126) [40] the NEWTON procedure failed to converge in
most cases.
, which corresponds to closing the system with a MAXWELLian distribution function
eqn. (2.126) [40] the NEWTON procedure failed to converge in
most cases.
Figure 2.4:
Comparison of the different closure relations
with the sixth moment from a Monte Carlo
simulation.
|
 |
Using  the closure relation becomes
the closure relation becomes
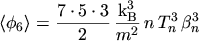 |
(2.177) |
and the full six moments transport model reads
In the following the equations for the six moments transport model are rewritten by
introducing the charge sign 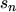 for electrons and the coefficients
for electrons and the coefficients 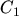 to
to 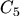 . The
balance equations become
. The
balance equations become
with
 |
(2.187) |
and the following flux equations:
The equations for holes are obtained by replacing 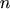 by
by 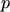 and taking into account that
and taking into account that 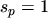 :
:
M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF
![]() called kurtosis has been
introduced, which is in this work defined as the deviation of the fourth moment of the
non-MAXWELL distribution function from the fourth moment of a MAXWELL distribution function with the
same standard deviation
called kurtosis has been
introduced, which is in this work defined as the deviation of the fourth moment of the
non-MAXWELL distribution function from the fourth moment of a MAXWELL distribution function with the
same standard deviation
![]() . Eqn. (2.126) is one
possible closure relation obtained from a MAXWELL distribution function. Other empirical
closures are also possible (eqn. (2.176)). By introducing an additional
temperature
. Eqn. (2.126) is one
possible closure relation obtained from a MAXWELL distribution function. Other empirical
closures are also possible (eqn. (2.176)). By introducing an additional
temperature ![]() 2.11
2.11
![]() the closure relation becomes
the closure relation becomes
![]() for electrons and the coefficients
for electrons and the coefficients ![]() to
to ![]() . The
balance equations become
. The
balance equations become
![]() by
by ![]() and taking into account that
and taking into account that ![]() :
: