



Next: Legierungsinhomogenität
Up: 6.1.2 Analytische Lösung
Previous: Akustische Phononen
Im Gegensatz zu den akustischen Phononen versagt bei optischen Phononen die Relaxationszeitnäherung aufgrund der relativ großen Phononenenergie.
Optische Phononen tragen nennenswert zum Energieaustausch mit dem Gitter bei.
Prinzipiell erfolgt die Wechselwirkung mit optischen Phononen wieder sowohl über den Deformationspotential- als auch den Piezoeffekt zufolge der optischen Verzerrung, die man sich als das gegenphasige Schwingen der Anion- und Kationuntergitter gegeneinander vorstellen kann.
Quantenmechanische Auswahlregeln verbieten die optische Deformationspotentialstreuung (ODP) für 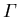 und X Täler. Da die L Täler bei III-V HL nicht das LB Minimum darstellen, hat ODP Streuung keinen Einfluß auf die Nullfeldbeweglichkeit.
und X Täler. Da die L Täler bei III-V HL nicht das LB Minimum darstellen, hat ODP Streuung keinen Einfluß auf die Nullfeldbeweglichkeit.
Die Kopplung über das Polarisationsfeld hingegen ist der dominante Streuprozeß in Verbindungshalbleitern für Temperaturen größer als etwa 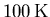 .
Meist wird die Bezeichnung polar-optische Phononenstreuung (PO) verwendet, die ODP Streuung wird auch als nichtpolar-optische Phononenstreuung bezeichnet.
Wie die piezoelektrische tritt die PO Streuung nur in polaren und nicht in Elementhalbleitern auf.
Bei
.
Meist wird die Bezeichnung polar-optische Phononenstreuung (PO) verwendet, die ODP Streuung wird auch als nichtpolar-optische Phononenstreuung bezeichnet.
Wie die piezoelektrische tritt die PO Streuung nur in polaren und nicht in Elementhalbleitern auf.
Bei 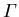 können wieder nur LO Phononen Elektronen streuen. Aus den in [42] angegebenen mittleren Energie- und Impulsverlustraten für PO Phononen und dem Gleichgewicht mit der mittleren Energie- und Impulszunahme
können wieder nur LO Phononen Elektronen streuen. Aus den in [42] angegebenen mittleren Energie- und Impulsverlustraten für PO Phononen und dem Gleichgewicht mit der mittleren Energie- und Impulszunahme![[*]](foot_motif.gif) aus dem elektrischen Feld,
aus dem elektrischen Feld,
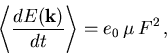 |
(6.22) |
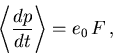 |
(6.23) |
kann im Grenzfall (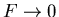 ,
, 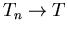 ) folgende Relation hergeleitet werden,
) folgende Relation hergeleitet werden,
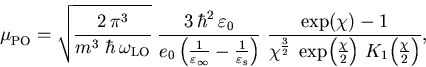 |
(6.24) |
wobei 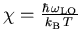 und K1 die modifizierte Besselfunktion zweiter Art bezeichnet.
und K1 die modifizierte Besselfunktion zweiter Art bezeichnet.
Die bestimmenden Größen sind die Elektronenmasse und die Phononenenergie 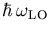 . Die Temperaturabhängigkeit ist im rechten Term von (6.24) enthalten.
. Die Temperaturabhängigkeit ist im rechten Term von (6.24) enthalten.




Next: Legierungsinhomogenität
Up: 6.1.2 Analytische Lösung
Previous: Akustische Phononen
Christian Koepf
1997-11-11
![[*]](foot_motif.gif) aus dem elektrischen Feld,
aus dem elektrischen Feld,
![]() .
Meist wird die Bezeichnung polar-optische Phononenstreuung (PO) verwendet, die ODP Streuung wird auch als nichtpolar-optische Phononenstreuung bezeichnet.
Wie die piezoelektrische tritt die PO Streuung nur in polaren und nicht in Elementhalbleitern auf.
Bei
.
Meist wird die Bezeichnung polar-optische Phononenstreuung (PO) verwendet, die ODP Streuung wird auch als nichtpolar-optische Phononenstreuung bezeichnet.
Wie die piezoelektrische tritt die PO Streuung nur in polaren und nicht in Elementhalbleitern auf.
Bei ![]() können wieder nur LO Phononen Elektronen streuen. Aus den in [42] angegebenen mittleren Energie- und Impulsverlustraten für PO Phononen und dem Gleichgewicht mit der mittleren Energie- und Impulszunahme
können wieder nur LO Phononen Elektronen streuen. Aus den in [42] angegebenen mittleren Energie- und Impulsverlustraten für PO Phononen und dem Gleichgewicht mit der mittleren Energie- und Impulszunahme![[*]](foot_motif.gif) aus dem elektrischen Feld,
aus dem elektrischen Feld,
![]() ,
, ![]() ) folgende Relation hergeleitet werden,
) folgende Relation hergeleitet werden,
![]() . Die Temperaturabhängigkeit ist im rechten Term von (6.24) enthalten.
. Die Temperaturabhängigkeit ist im rechten Term von (6.24) enthalten.