 |
Man könnte vielleicht meinen, daß der Fehler von einer Überschätzung der Ladungsträgerenergie durch die Verwerfungsmethode (6.54) herrührt, da die BH Streurate im wesentlichen mit einer Potenz der Energie sinkt.
Das Pauli Prinzip , in der MC Simulation repräsentiert durch die Verwerfungsmethode, bewirkt ja, daß die Elektronen im wesentlichen nur um und über der Fermienergie gestreut werden und so die Streurate in diesem Energiebereich abtasten.
In Abbildung 6.9 ist die mittlere Ladungsträgerenergie ![]() , die durch
, die durch
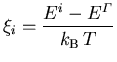 .
.
Der Zusammenhang zwischen ![]() und
und ![]() ist durch die zweite Abszissenskala in Abbildung 6.9 gegeben.
Für schwache Dotierung (
ist durch die zweite Abszissenskala in Abbildung 6.9 gegeben.
Für schwache Dotierung (![]() ) liegt die Ladungsträgerenergie aufgrund der Nichtparabolizität etwas über
) liegt die Ladungsträgerenergie aufgrund der Nichtparabolizität etwas über ![]() . Mit steigendem Grad der Entartung nimmt die Gleichgewichtsenergie deutlich zu.
Bemerkenswert ist, daß ab ca.
. Mit steigendem Grad der Entartung nimmt die Gleichgewichtsenergie deutlich zu.
Bemerkenswert ist, daß ab ca. ![]() das L Tal populiert wird (die Talseparation ist
das L Tal populiert wird (die Talseparation ist ![]() ) und daß die Gesamtenergie aufgrund der potentiellen Energie der L Elektronen stärker zunimmt.
Da diese eine geringere Beweglichkeit haben, nimmt
) und daß die Gesamtenergie aufgrund der potentiellen Energie der L Elektronen stärker zunimmt.
Da diese eine geringere Beweglichkeit haben, nimmt ![]() nach dem relativen Maximum mit steigender Dotierung wieder ab (Abbildung 6.8).
Wenn man nur das
nach dem relativen Maximum mit steigender Dotierung wieder ab (Abbildung 6.8).
Wenn man nur das ![]() Tal betrachtet, steigt die Beweglichkeit in diesem monoton an.
Tal betrachtet, steigt die Beweglichkeit in diesem monoton an.
Die höhere Ladungsträgerenergie aufgrund der Entartung darf nicht mit einer Erhöhung der Elektronentemperatur , die in die Verteilungsfunktion eingeht, assoziiert werden. Die Ladungsträger befinden sich nach wie vor im Equilibrium und folglich auf Gittertemperatur. Da sowohl die Gesamtenergie wie auch die Energie der Elektronen in den Tälern sehr gut mit den theoretisch erwarteten übereinstimmen, ist die Schlußfolgerung legitim, daß die verwendete Methode zur Berücksichtigung der Entartung in den MC Rechnungen die Verteilungsfunktion korrekt wiedergibt und daß daher der Grund für die Nichtübereinstimmung mit dem Experiment tatsächlich in den Schwächen der Coulombstreurate und anderen physikalischen Modellen liegt.
 |
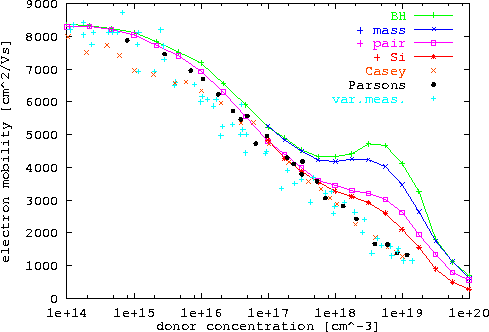
Die Berücksichtigung der konzentrationsabhängigen Änderung der LB Dispersion und Erhöhung der Zustandsdichte, die durch eine Erhöhung der effektiven Masse als Funktion von n modelliert wird (siehe Abschnitt 5.2.4), reduziert ![]() bei konstanter Konzentration und verkleinert somit den Fehler etwas (Kurve +mass in Abbildung 6.8).
Einen wesentlichen Effekt hat die Berücksichtigung der kohärenten Paarstreuung (Kurve +pair in Abbildung 6.8).
Im entarteten Bereich wird die Übereinstimmung mit den experimentellen Daten stark verbessert, aber auch im Bereich niedriger Dotierung liefert diese Korrektur eine nennenswerte Verbesserung.
Eine weitere Absenkung der Beweglichkeit bei hohen Dotierungen bringt die Verwendung des Formfaktors, erkenntlich am Beispiel von Dotierung mit Si (Kurve +Si in Abbildung 6.8).
bei konstanter Konzentration und verkleinert somit den Fehler etwas (Kurve +mass in Abbildung 6.8).
Einen wesentlichen Effekt hat die Berücksichtigung der kohärenten Paarstreuung (Kurve +pair in Abbildung 6.8).
Im entarteten Bereich wird die Übereinstimmung mit den experimentellen Daten stark verbessert, aber auch im Bereich niedriger Dotierung liefert diese Korrektur eine nennenswerte Verbesserung.
Eine weitere Absenkung der Beweglichkeit bei hohen Dotierungen bringt die Verwendung des Formfaktors, erkenntlich am Beispiel von Dotierung mit Si (Kurve +Si in Abbildung 6.8).
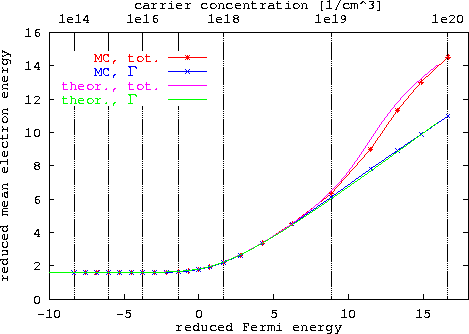
In Abbildung 6.10 ist die Abhängigkeit der Beweglichkeit vom Donatorelement gezeigt. Die Meßdaten sind aus [30,121,166,211] beziehungsweise [129] entnommen.
Neben den beiden schon in der vorigen Abbildung enthaltenen Kurven, nämlich dem nicht dopandenspezifischen verbesserten BH Modell (+pair) und der Kurve inklusive des Formfaktors für Si, sind gerechnete Kurven für die Donatoren Se und Sn gezeigt.
Für ![]() hat F(q) keinen Einfluß, daher ist in der Folge auch nur der Hochkonzentrationsbereich dargestellt.
Mit steigender Dotierung wird die Korrektur von
hat F(q) keinen Einfluß, daher ist in der Folge auch nur der Hochkonzentrationsbereich dargestellt.
Mit steigender Dotierung wird die Korrektur von ![]() größer, wobei sie mit wachsender Ordnungszahl Z betragsmäßig zunimmt. Für konstante Dotierungskonzentration nimmt die Beweglichkeit in der Reihenfolge der Dotierungselemente Si, Se und Sn ab.
Dies kann durch den funktionalen Verlauf des Formfaktors erklärt werden, da die effektiv wirksame Ladung Z-F(q) in den Streugrößen (vgl. (6.45)) immer größer als +1, dem Wert für einwertige Donatoren bei Vernachlässigung von F(q), also
größer, wobei sie mit wachsender Ordnungszahl Z betragsmäßig zunimmt. Für konstante Dotierungskonzentration nimmt die Beweglichkeit in der Reihenfolge der Dotierungselemente Si, Se und Sn ab.
Dies kann durch den funktionalen Verlauf des Formfaktors erklärt werden, da die effektiv wirksame Ladung Z-F(q) in den Streugrößen (vgl. (6.45)) immer größer als +1, dem Wert für einwertige Donatoren bei Vernachlässigung von F(q), also ![]() , ist (vgl. Abbildung 6.11).
, ist (vgl. Abbildung 6.11).
Die Abhängigkeit der Beweglichkeit von der Dopandenart wurde bisher in der Literatur nur experimentell untersucht und für Verbindungshalbleiter wohl auch aufgrund der Streuung der Meßwerte generell für vernachlässigbar gehalten [127].
In Si hingegen sind dopandenspezifische Unterschiede in ![]() eindeutig experimentell nachgewiesen worden [141]. Dotierung mit As (Z=33) führt zu kleineren Werten als mit P (Z=15) , was ebenfalls durch das Modell klar bestätigt wird [103].
Für das Beispiel GaAs weisen die Vorhersagen der Rechnung bezüglich der Verschiedenheit von
eindeutig experimentell nachgewiesen worden [141]. Dotierung mit As (Z=33) führt zu kleineren Werten als mit P (Z=15) , was ebenfalls durch das Modell klar bestätigt wird [103].
Für das Beispiel GaAs weisen die Vorhersagen der Rechnung bezüglich der Verschiedenheit von ![]() als Funktion von Z durchaus dieselbe ``Schwankungsbreite'' wie die Meßdaten auf und insofern besteht kein Widerspruch zum Experiment.
als Funktion von Z durchaus dieselbe ``Schwankungsbreite'' wie die Meßdaten auf und insofern besteht kein Widerspruch zum Experiment.
Die gegenständliche Untersuchung zeigt aber die Bedeutung der Simulation als numerisches Experiment, das unter wohldefinierten Rahmenbedingungen und für ideale Proben Zusammenhänge untersuchen kann, die einer meßtechnischen Identifizierung nur schwer zugänglich sind.
Die analytische Modellierung des Einflusses der Donatorenspezies auf ![]() , welcher erst im entarteten Bereich einsetzt, kann durch Erweiterung von (6.39) um einen rationalen Term erfolgen, der den Einfluß der Spezies ausgedrückt durch die Abhängigkeit von Z berücksichtigt:
, welcher erst im entarteten Bereich einsetzt, kann durch Erweiterung von (6.39) um einen rationalen Term erfolgen, der den Einfluß der Spezies ausgedrückt durch die Abhängigkeit von Z berücksichtigt:
 |
Die naheliegende Möglichkeit zur Erklärung der verbleibenden Diskrepanz zwischen den MC Rechnungen und experimentellen Daten im Bereich ![]() ist die Berücksichtigung von Kompensationseffekten.
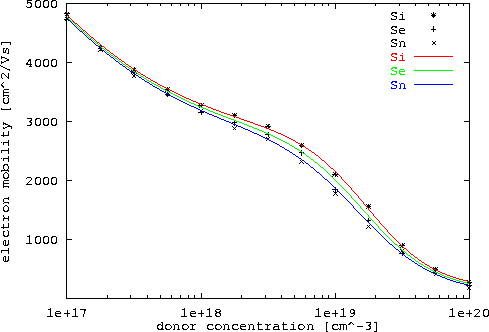
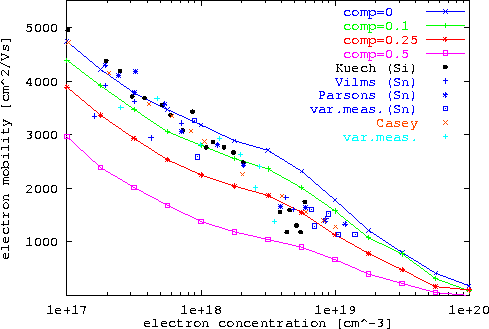
Abbildung 6.13 zeigt die Beweglichkeit für verschiedene konstante Werte des Kompensationsgrades
ist die Berücksichtigung von Kompensationseffekten.
Abbildung 6.13 zeigt die Beweglichkeit für verschiedene konstante Werte des Kompensationsgrades ![]() unter Verwendung des verfeinerten Modells am Beispiel von Dotierung mit Sn.
Die Abszisse ist nunmehr die Ladungsträgerkonzentration, die bei Kompensation gleich der Nettodotierung ist.
Mit steigendem
unter Verwendung des verfeinerten Modells am Beispiel von Dotierung mit Sn.
Die Abszisse ist nunmehr die Ladungsträgerkonzentration, die bei Kompensation gleich der Nettodotierung ist.
Mit steigendem ![]() sinkt der Abschirmungseffekt,
sinkt der Abschirmungseffekt, ![]() und natürlich auch
und natürlich auch ![]() .
.
 |
 |
Um die vorliegenden experimentellen Daten zu erklären, ist, wie aus den Kurven ersichtlich, ein mit der Dotierung zunehmender Kompensationsgrad nötig.
Genau das liefert der Effekt der Autokompensation .
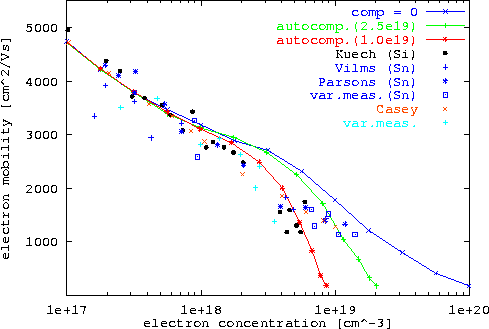
In Abbildung 6.14 sind Kurven für Autokompensation von Si und Sn neben dem unkompensierten Fall (Sn) gezeigt.
Die dabei verwendeten Parameterwerte für ![]() entsprechen in etwa den experimentell beobachteten, tatsächlich erreichbaren Maximalkonzentrationen für Dotierung mit Si (
entsprechen in etwa den experimentell beobachteten, tatsächlich erreichbaren Maximalkonzentrationen für Dotierung mit Si (![]() ) und Sn (
) und Sn (![]() ) [181].
) [181].
Obwohl das benutzte einfache Modell (6.41) die Kompensation bei schwacher Dotierung unterschätzt und dann einen zu starken Anstieg hin zur Sättigungskonzentration ![]() aufweist, kann doch eine zufriedenstellende Übereinstimmung mit dem Experiment erreicht werden.
aufweist, kann doch eine zufriedenstellende Übereinstimmung mit dem Experiment erreicht werden.