



Next: Ein hydrodynamisches Beweglichkeitsmodell für GaInAs
Up: 6.1.9 Einfluß des elektrischen
Previous: 6.1.9 Einfluß des elektrischen
Prinzipiell sind bei der Modellierung des Hochfeldtransports in HL mit Mehrtalbandstruktur zwei Ansätze möglich: Die Einführung der Ladungsträgergrößen der einzelnen Täler (Konzentration, Energie etc.) als unabhängige Variablen in den Transportgleichungen.
Dies impliziert Formulierungen der abhängigen physikalischen Parameter wie Beweglichkeit etc. für die talspezifischen Variablen als Funktionen der externer Größen [28].
Die Teilchenübergänge zwischen den Tälern werden so zu Generations-/Rekombinationstermen, für die zusätzliche Modelle gefunden werden müssen, die kaum oder nur schwer experimentell unterlegbar sind.
Dieser Ansatz erhöht nicht nur die Anzahl der Unabhängigen und Differentialgleichungen sondern auch die Modellkomplexität enorm und wird daher in der Praxis kaum verfolgt.
Der alternative, auf den ersten Blick vielleicht physikalisch weniger motivierte Weg besteht in der Beibehaltung des Bildes eines einzelnen Elektronengases unter Berücksichtigung der Mehrtalbandstruktur in der Modellierung durch effektive Größen des gesamten Ladungsträgerensembles.
Diese Vorstellung wird auch in der Folge benutzt.
Die Modellierung des Feldeinflusses auf die Beweglichkeit im Fall des DD Transportmodells geschieht allgemein durch eine Formulierung 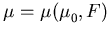 .Das heißt, man nimmt eine Trennung vor in die Nullfeldbeweglichkeit
.Das heißt, man nimmt eine Trennung vor in die Nullfeldbeweglichkeit 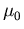 inklusive aller Gitter-, Legierungs- und Dotierungsabhängigkeiten und eine explizite Abhängigkeit vom Betrag der treibenden elektrischen Kraft
inklusive aller Gitter-, Legierungs- und Dotierungsabhängigkeiten und eine explizite Abhängigkeit vom Betrag der treibenden elektrischen Kraft
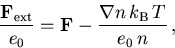 |
(6.68) |
die unter homogenen Bedingungen dem elektrischen Feld 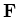 gleich ist.
gleich ist.
Meist wird für III-V HL der Ansatz [131]
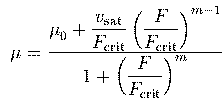 |
(6.69) |
gebraucht, welcher durch die Dotierungsunabhängigkeit der Sättigungsgeschwindigkeit motiviert ist.
(6.69) ist eine rein empirische Beschreibung der effektiven Beweglichkeit, die den Zwischentaltransfer implizit enthält.
Die Parameter 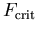 und m bestimmen die Lage des Maximums von
und m bestimmen die Lage des Maximums von 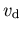 und die Steilheit des Übergangs vom linearen Verlauf
und die Steilheit des Übergangs vom linearen Verlauf 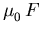 zu
zu  .
Eine konzeptuell gleiche Beschreibung mit zusätzlichen Abhängigkeiten der Modellparameter
.
Eine konzeptuell gleiche Beschreibung mit zusätzlichen Abhängigkeiten der Modellparameter  und m von
und m von 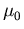 wurde in [223] vorgeschlagen, um die Meßwerte genauer wiederzugeben.
Eine andere Berechnung für die effektive Gesamtbeweglichkeit basierend auf der Beschreibung eines Zweitalsystems mit feldabhängiger Kopplung unter Einhaltung von Teilchen- und Energieerhaltung wurde in [131] vorgeschlagen.
wurde in [223] vorgeschlagen, um die Meßwerte genauer wiederzugeben.
Eine andere Berechnung für die effektive Gesamtbeweglichkeit basierend auf der Beschreibung eines Zweitalsystems mit feldabhängiger Kopplung unter Einhaltung von Teilchen- und Energieerhaltung wurde in [131] vorgeschlagen.
Die Formulierung der Beweglichkeit im Rahmen des hydrodynamischen (HD) oder Energietransportmodells wird allgemein durch einen Ansatz 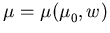 vorgenommen.
Die Abhängigkeit von
vorgenommen.
Die Abhängigkeit von 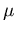 vom elektrischen Feld ist hier implizit in der Feldabhängigkeit der Ladungsträgerenergie
vom elektrischen Feld ist hier implizit in der Feldabhängigkeit der Ladungsträgerenergie 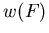 enthalten.
Dieser Zusammenhang ist nichtlokal, wenn
enthalten.
Dieser Zusammenhang ist nichtlokal, wenn 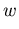 aus der Lösung der Energiebilanzgleichung in der HD Simulation resultiert.
Zum Zweck der Modellierung wird Homogenität des Feldes angenommen und man hat somit wieder einen eindeutigen, üblicherweise monotonen Zusammenhang
aus der Lösung der Energiebilanzgleichung in der HD Simulation resultiert.
Zum Zweck der Modellierung wird Homogenität des Feldes angenommen und man hat somit wieder einen eindeutigen, üblicherweise monotonen Zusammenhang 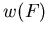 .
.
Unter speziellen Bedingungen können HD und DD Formulierung von 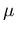 eindeutig ineinander übergeführt werden.
Nimmt man an, daß das Abklingen der mittleren Impulskomponente in Feldrichtung p zum Gleichgewichtswert Null mit der Impulsrelaxationszeit
eindeutig ineinander übergeführt werden.
Nimmt man an, daß das Abklingen der mittleren Impulskomponente in Feldrichtung p zum Gleichgewichtswert Null mit der Impulsrelaxationszeit 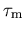 erfolgt,
erfolgt,
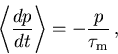 |
(6.70) |
und berücksichtigt man die Definition der Beweglichkeit (6.16), so stellt die Impulsbilanz (6.23) unter stationären homogenen Bedingungen die Stromrelation
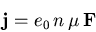 |
(6.71) |
dar. Nimmt man in gleicher Weise eine Relaxation der mittleren Energie zum Gleichgewichtswert 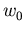 mit der Energierelaxationszeit
mit der Energierelaxationszeit 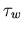 an,
an,
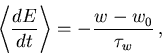 |
(6.72) |
so lautet die stationäre Energiebilanz (6.22)
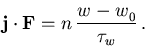 |
(6.73) |
Die Größen 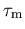 und
und 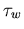 sind im Prinzip von den im HD Modell berücksichtigten ersten vier Momenten der Distribution (
sind im Prinzip von den im HD Modell berücksichtigten ersten vier Momenten der Distribution (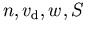 ) abhängig, und können im Rahmen eines selbstkonsistenten Systems daher nicht frei gewählt werden.
Hänsch hat gezeigt, daß man unter Verwendung eines DD Modells für
) abhängig, und können im Rahmen eines selbstkonsistenten Systems daher nicht frei gewählt werden.
Hänsch hat gezeigt, daß man unter Verwendung eines DD Modells für 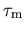 bzw.
bzw. 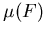 , das den Sättigungsverlauf der Driftgeschwindigkeit in Si gut beschreibt, den einfachen Zusammenhang
, das den Sättigungsverlauf der Driftgeschwindigkeit in Si gut beschreibt, den einfachen Zusammenhang
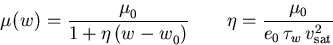 |
(6.74) |
für die HD Beweglichkeit mit einer konstanten Energierelaxationszeit erhält [77].
Die Gleichungen (6.71) und (6.73) geben den expliziten 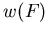 Zusammenhang unter Verwendung der erwähnten Modelle für
Zusammenhang unter Verwendung der erwähnten Modelle für 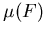 und
und 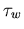 .
Weitab vom Gleichgewicht ist
.
Weitab vom Gleichgewicht ist 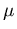 umgekehrt proportional zu
umgekehrt proportional zu 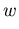 ,
, 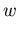 steigt linear mit F, was einer Ladungsträgerbewegung mit konstanter Driftgeschwindigkeit
steigt linear mit F, was einer Ladungsträgerbewegung mit konstanter Driftgeschwindigkeit  entspricht.
entspricht.




Next: Ein hydrodynamisches Beweglichkeitsmodell für GaInAs
Up: 6.1.9 Einfluß des elektrischen
Previous: 6.1.9 Einfluß des elektrischen
Christian Koepf
1997-11-11
![]() .Das heißt, man nimmt eine Trennung vor in die Nullfeldbeweglichkeit
.Das heißt, man nimmt eine Trennung vor in die Nullfeldbeweglichkeit ![]() inklusive aller Gitter-, Legierungs- und Dotierungsabhängigkeiten und eine explizite Abhängigkeit vom Betrag der treibenden elektrischen Kraft
inklusive aller Gitter-, Legierungs- und Dotierungsabhängigkeiten und eine explizite Abhängigkeit vom Betrag der treibenden elektrischen Kraft
![]() vorgenommen.
Die Abhängigkeit von
vorgenommen.
Die Abhängigkeit von ![]() vom elektrischen Feld ist hier implizit in der Feldabhängigkeit der Ladungsträgerenergie
vom elektrischen Feld ist hier implizit in der Feldabhängigkeit der Ladungsträgerenergie ![]() enthalten.
Dieser Zusammenhang ist nichtlokal, wenn
enthalten.
Dieser Zusammenhang ist nichtlokal, wenn ![]() aus der Lösung der Energiebilanzgleichung in der HD Simulation resultiert.
Zum Zweck der Modellierung wird Homogenität des Feldes angenommen und man hat somit wieder einen eindeutigen, üblicherweise monotonen Zusammenhang
aus der Lösung der Energiebilanzgleichung in der HD Simulation resultiert.
Zum Zweck der Modellierung wird Homogenität des Feldes angenommen und man hat somit wieder einen eindeutigen, üblicherweise monotonen Zusammenhang ![]() .
.![]() eindeutig ineinander übergeführt werden.
Nimmt man an, daß das Abklingen der mittleren Impulskomponente in Feldrichtung p zum Gleichgewichtswert Null mit der Impulsrelaxationszeit
eindeutig ineinander übergeführt werden.
Nimmt man an, daß das Abklingen der mittleren Impulskomponente in Feldrichtung p zum Gleichgewichtswert Null mit der Impulsrelaxationszeit ![]() erfolgt,
erfolgt,
![]() Zusammenhang unter Verwendung der erwähnten Modelle für
Zusammenhang unter Verwendung der erwähnten Modelle für ![]() und
und ![]() .
Weitab vom Gleichgewicht ist
.
Weitab vom Gleichgewicht ist ![]() umgekehrt proportional zu
umgekehrt proportional zu ![]() ,
, ![]() steigt linear mit F, was einer Ladungsträgerbewegung mit konstanter Driftgeschwindigkeit
steigt linear mit F, was einer Ladungsträgerbewegung mit konstanter Driftgeschwindigkeit ![]() entspricht.
entspricht.