



Next: Verspannungsabhängigkeit im Hochfeldtransport
Up: 6.1.9 Einfluß des elektrischen
Previous: Modellierung
Aufgrund der Mehrtalbandstruktur der Verbindungshalbleiter und der resultierenden Repopulation im Hochfeldbereich beobachtet man eine völlig andere Abhängigkeit 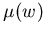 als (6.74) wiedergibt.
Auch die Beschreibung der Ladungsträgerenergie ändert sich.
Die gesamte mittlere Energie pro Ladungsträger ist allgemein
als (6.74) wiedergibt.
Auch die Beschreibung der Ladungsträgerenergie ändert sich.
Die gesamte mittlere Energie pro Ladungsträger ist allgemein
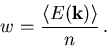 |
(6.75) |
In einem Eintalsystem ist die Aufteilung in Driftenergie 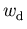 (kinetische Energie im engeren Sinn) und thermische Energie
(kinetische Energie im engeren Sinn) und thermische Energie 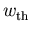 naheliegend,
naheliegend,
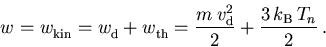 |
(6.76) |
Die in (6.76) definierte Ladungsträgertemperatur Tn ist dabei keine absolute Temperatur des Elektronengases im thermodynamischen Sinn.
Mit Ausnahme tiefer Gittertemperaturen ist der Driftterm vernachlässigbar, also 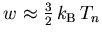 .
Es sei auch darauf hingewiesen, daß nur für parabolische Täler der Zusammenhang
.
Es sei auch darauf hingewiesen, daß nur für parabolische Täler der Zusammenhang 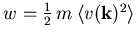 gilt.
In einem Mehrtalsystem kommt zur kinetischen noch die potentielle Energie der Ladungsträger in den höheren Minima hinzu, sodaß
gilt.
In einem Mehrtalsystem kommt zur kinetischen noch die potentielle Energie der Ladungsträger in den höheren Minima hinzu, sodaß
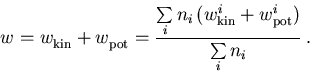 |
(6.77) |
Die potentielle Energie ist die Differenz des jeweiligen Talminimums zum absoluten Bandminimum, 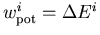 , ni bezeichnet die relative Besetzung (Population) des Tales i.
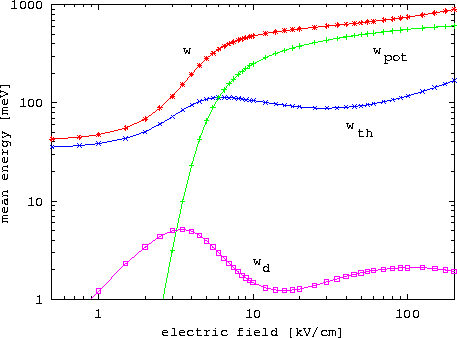
In Abbildung 6.27 sind die verschiedenen Beiträge der Drift-, thermischen und potentiellen Energie zur Gesamtenergie am Beispiel von Ga0.47In0.53As illustriert.
Neben der Tatsache, daß zumindest bei Raumtemperatur der Driftterm vernachlässigbar ist, beobachtet man die mit zunehmendem Feld dominanter werdende Rolle von
, ni bezeichnet die relative Besetzung (Population) des Tales i.
In Abbildung 6.27 sind die verschiedenen Beiträge der Drift-, thermischen und potentiellen Energie zur Gesamtenergie am Beispiel von Ga0.47In0.53As illustriert.
Neben der Tatsache, daß zumindest bei Raumtemperatur der Driftterm vernachlässigbar ist, beobachtet man die mit zunehmendem Feld dominanter werdende Rolle von 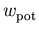 aufgrund der Besetzung der höheren Minima.
Die Gesamtenergie
aufgrund der Besetzung der höheren Minima.
Die Gesamtenergie 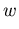 wird mittels der Definition
wird mittels der Definition 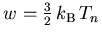 auch in den HD Transportgleichungen synonym mit der Ladungsträgertemperatur verwendet.
auch in den HD Transportgleichungen synonym mit der Ladungsträgertemperatur verwendet.
Abbildung 6.27:
Beiträge zur mittleren Elektronenenergie in Ga0.47In0.53As als Funktion des elektrischen Feldes
 |
Eine weitere wichtige Größe ist die Energierelaxationszeit . Während diese im Modell (6.74) eine konstante, also von den Momenten unabhängige Größe ist, scheint diese Annahme zumindest bei Verbindungshalbleitern fragwürdig.
Durch die Beziehung (6.73) kann man 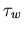 mit MC Simulationen direkt auswerten.
Am Beispiel von GaAs sind in Abbildung 6.28 sowohl die Relaxationszeiten für die individuellen Minima wie auch der Gesamtwert von
mit MC Simulationen direkt auswerten.
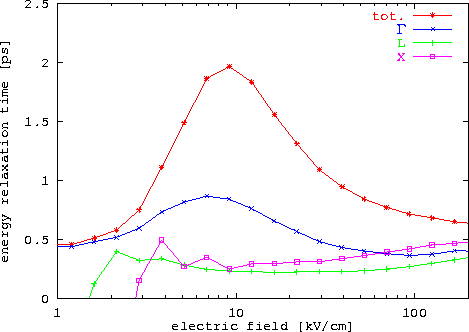
Am Beispiel von GaAs sind in Abbildung 6.28 sowohl die Relaxationszeiten für die individuellen Minima wie auch der Gesamtwert von 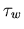 als Funktion der elektrischen Feldstärke dargestellt.
als Funktion der elektrischen Feldstärke dargestellt.
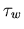 erhöht sich vom üblicherweise benutzten Wert von 0.5 ps bis um den Faktor 4 bei mittleren Feldern.
erhöht sich vom üblicherweise benutzten Wert von 0.5 ps bis um den Faktor 4 bei mittleren Feldern.
Abbildung 6.28:
Energierelaxationszeit in GaAs als Funktion des elektrischen Feldes
 |
Um die Mehrtalbandstruktur einzubeziehen, kann man ein Modell konzipieren, das eine Beschreibung der Einzelbeweglichkeit der Täler, 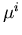 , und deren Kombination über die Besetzung jeweils als Funktion von
, und deren Kombination über die Besetzung jeweils als Funktion von 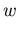 beinhaltet [109].
In Anlehnung an (6.74) wird die Beweglichkeit im Tal i angesetzt als
beinhaltet [109].
In Anlehnung an (6.74) wird die Beweglichkeit im Tal i angesetzt als
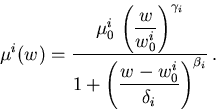 |
(6.78) |
Darin ist 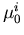 die Nullfeldbeweglichkeit und
die Nullfeldbeweglichkeit und 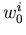 die Gleichgewichtsenergie im Minimum i.
Die anderen Modellparameter haben zum Teil physikalische Bedeutung, sind aber besonders bei den höheren Minima auch Anpassungsparameter.
So beschreibt der Exponent
die Gleichgewichtsenergie im Minimum i.
Die anderen Modellparameter haben zum Teil physikalische Bedeutung, sind aber besonders bei den höheren Minima auch Anpassungsparameter.
So beschreibt der Exponent 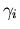 die Energieabhängigkeit der Beweglichkeit im Bereich der warmen Elektronen bevor Zwischentaltransfer auftritt.
Für die PO dominierten III-V HL ist daher
die Energieabhängigkeit der Beweglichkeit im Bereich der warmen Elektronen bevor Zwischentaltransfer auftritt.
Für die PO dominierten III-V HL ist daher 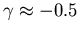 .
Der Parameter
.
Der Parameter 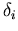 ist die Energie bei der Zwischentaltransfer einsetzt, also ungefähr die Energiedifferenz der Minima.
Im anschließenden Bereich der starken Zwischentalstreuung fällt
ist die Energie bei der Zwischentaltransfer einsetzt, also ungefähr die Energiedifferenz der Minima.
Im anschließenden Bereich der starken Zwischentalstreuung fällt 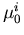 steil mit dem Exponenten
steil mit dem Exponenten 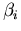 ab (vgl. Abbildung 6.29).
Die Gesamtbeweglichkeit ist die mit der Besetzung gewichtete Summe der Einzelbeweglichkeiten,
ab (vgl. Abbildung 6.29).
Die Gesamtbeweglichkeit ist die mit der Besetzung gewichtete Summe der Einzelbeweglichkeiten,
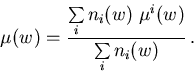 |
(6.79) |
Zur Abschätzung der Population der Täler kann man eine modifizierte Maxwell-
Boltzmann Verteilung ansetzten. Dies führt auf die Besetzung der höheren Minima relativ zu 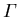 in der Form
in der Form
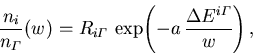 |
(6.80) |
Der Vorfaktor a in der Exponentialfunktion stellt die unterschiedliche Energieskalierung dar, da anstelle der kinetischen Energie, repräsentiert durch die Elektronentemperatur, ebenfalls die Gesamtenergie 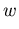 als bestimmende Größe in f herangezogen wird.
Da
als bestimmende Größe in f herangezogen wird.
Da 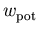 und damit auch
und damit auch 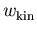 für
für 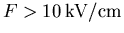 ungefähr proportional zu
ungefähr proportional zu 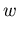 sind (vgl. Abbildung 6.27), kann a näherungsweise konstant angenommen werden.
sind (vgl. Abbildung 6.27), kann a näherungsweise konstant angenommen werden.
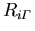 ist der Entartungsfaktor des Minimums i bezogen auf
ist der Entartungsfaktor des Minimums i bezogen auf 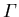 (siehe (6.59)).
Die Beweglichkeit
(siehe (6.59)).
Die Beweglichkeit 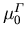 wurde schon in Abschnitt 6.1.5 behandelt.
Die restlichen Modellparameter, die aus MC Simulationsergebnissen durch nichtlineare Regression gewonnen wurden, sind in Tabelle 6.2 angeführt.
wurde schon in Abschnitt 6.1.5 behandelt.
Die restlichen Modellparameter, die aus MC Simulationsergebnissen durch nichtlineare Regression gewonnen wurden, sind in Tabelle 6.2 angeführt.
Tabelle 6.2:
Parameter des HD Beweglichkeitsmodells für GaxIn1-xAs
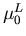 |
[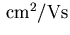 ] ] |
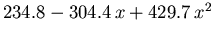 |
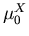 |
[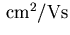 ] ] |
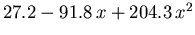 |
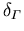 |
[meV] |
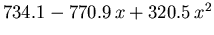 |
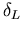 |
[meV] |
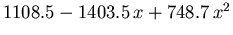 |
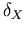 |
[meV] |
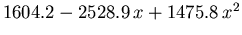 |
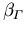 |
|
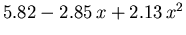 |
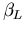 |
|
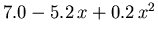 |
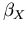 |
|
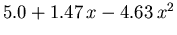 |
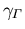 |
|
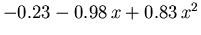 |
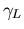 |
|
0 |
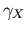 |
|
0 |
| a |
|
4.0 |
In Abbildung 6.29 sind die MC Daten und die vom beschriebenen Modell gelieferten Werte für die Einzel- und Gesamtbeweglichkeit in Ga0.47In0.53As dargestellt.
Auffällig ist, daß die Nullfeldbeweglichkeit der L und X Täler bei niedrigen Energien nicht gut definiert sind, was darauf zurückzuführen ist, daß diese Minima bei schwachen Feldern kaum besetzt sind, 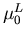 und
und 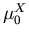 sind eigentlich künstliche Größen.
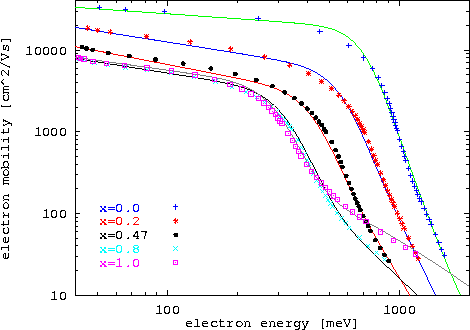
Abbildung 6.30 zeigt einen Vergleich der Gesamtbeweglichkeit des HD Modells in GaxIn1-xAs für verschiedene Legierungskonzentrationen. Auch hier ist die Übereinstimmung zwischen dem Modell und den MC Werten sehr gut.
sind eigentlich künstliche Größen.
Abbildung 6.30 zeigt einen Vergleich der Gesamtbeweglichkeit des HD Modells in GaxIn1-xAs für verschiedene Legierungskonzentrationen. Auch hier ist die Übereinstimmung zwischen dem Modell und den MC Werten sehr gut.
Abbildung 6.29:
Elektronenbeweglichkeit in Ga0.47In0.53As als Funktion der mittleren Elektronenenergie für die Einzelminima und gesamt. Die Symbole sind MC Daten, die durchgezogenen Linien Ergebnisse des analytischen Modells (6.78)-(6.80).
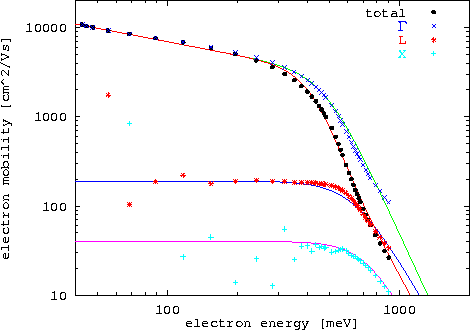 |
Abbildung 6.30:
Elektronenbeweglichkeit in GaxIn1-xAs als Funktion der mittleren Elektronenenergie für verschiedene Legierungskonzentrationen. Die Symbole sind MC Daten, die durchgezogenen Linien Ergebnisse des analytischen Modells (6.78)-(6.80).
 |




Next: Verspannungsabhängigkeit im Hochfeldtransport
Up: 6.1.9 Einfluß des elektrischen
Previous: Modellierung
Christian Koepf
1997-11-11

![]() mit MC Simulationen direkt auswerten.
Am Beispiel von GaAs sind in Abbildung 6.28 sowohl die Relaxationszeiten für die individuellen Minima wie auch der Gesamtwert von
mit MC Simulationen direkt auswerten.
Am Beispiel von GaAs sind in Abbildung 6.28 sowohl die Relaxationszeiten für die individuellen Minima wie auch der Gesamtwert von ![]() als Funktion der elektrischen Feldstärke dargestellt.
als Funktion der elektrischen Feldstärke dargestellt.
![]() erhöht sich vom üblicherweise benutzten Wert von 0.5 ps bis um den Faktor 4 bei mittleren Feldern.
erhöht sich vom üblicherweise benutzten Wert von 0.5 ps bis um den Faktor 4 bei mittleren Feldern. ![]() , und deren Kombination über die Besetzung jeweils als Funktion von
, und deren Kombination über die Besetzung jeweils als Funktion von ![]() beinhaltet [109].
In Anlehnung an (6.74) wird die Beweglichkeit im Tal i angesetzt als
beinhaltet [109].
In Anlehnung an (6.74) wird die Beweglichkeit im Tal i angesetzt als
![]() und
und ![]() sind eigentlich künstliche Größen.
Abbildung 6.30 zeigt einen Vergleich der Gesamtbeweglichkeit des HD Modells in GaxIn1-xAs für verschiedene Legierungskonzentrationen. Auch hier ist die Übereinstimmung zwischen dem Modell und den MC Werten sehr gut.
sind eigentlich künstliche Größen.
Abbildung 6.30 zeigt einen Vergleich der Gesamtbeweglichkeit des HD Modells in GaxIn1-xAs für verschiedene Legierungskonzentrationen. Auch hier ist die Übereinstimmung zwischen dem Modell und den MC Werten sehr gut.
