3.1.4 Das Transportmodell für Zweibandhalbleiter




Next: 3.2 Der Schottkykontakt
Up: 3.1 Die Halbleitergleichungen
Previous: 3.1.3 Einbeziehung nichtlokaler Effekte
Während es für Silizium gerechtfertigt ist, in der Beschreibung der
Transporteigenschaften im Rahmen der erweiterten Drift-Diffusionsnäherung
die Bandstruktur auf ein parabolisches Band zu reduzieren, ist eine derartige
Annahme bei Galliumarsenid nur im Bereich sehr kleiner Feldstärken
(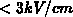 ) zulässig. Eine Betrachtung der Bandstruktur
(Abb. 3.10) legt jedoch nahe, den Elektronentransport mithilfe
eines Zweibandmodells zu beschreiben (siehe Kap. 3.4.1). Das würde
aber bedeuten, beide Bänder getrennt zu behandeln und für jedes
Band eine eigene Transport- und Erhaltungsgleichung zusammen mit
der Poissongleichung zu lösen. Dazu käme im einfachsten Fall noch eine
Beschreibung des Teilchentransfers zwischen den beiden Bändern.
Allerdings erfordert diese Methode beträchtlichen Mehraufwand bei der
numerischen Lösung des resultierenden Gleichungssystems, und eine effiziente
Implementierung in einen bestehenden Simulator, der auf der
Drift-Diffusionsnäherung basiert, ist nur schwer möglich.
) zulässig. Eine Betrachtung der Bandstruktur
(Abb. 3.10) legt jedoch nahe, den Elektronentransport mithilfe
eines Zweibandmodells zu beschreiben (siehe Kap. 3.4.1). Das würde
aber bedeuten, beide Bänder getrennt zu behandeln und für jedes
Band eine eigene Transport- und Erhaltungsgleichung zusammen mit
der Poissongleichung zu lösen. Dazu käme im einfachsten Fall noch eine
Beschreibung des Teilchentransfers zwischen den beiden Bändern.
Allerdings erfordert diese Methode beträchtlichen Mehraufwand bei der
numerischen Lösung des resultierenden Gleichungssystems, und eine effiziente
Implementierung in einen bestehenden Simulator, der auf der
Drift-Diffusionsnäherung basiert, ist nur schwer möglich.
Ein anderer Weg besteht darin, die Kopplung der Bänder ausgehend von
einer getrennten Beschreibung der Teilchen- und Energieerhaltung
im jeweiligen Band zu berechnen, und
durch eine effektive Beweglichkeit auszudrücken. Darüberhinaus erhält man
auch die Formulierung
einer effektiven mittleren Energie, die durch eine effektive Temperaturspannung
ausgedrückt wird. Dieser Weg wurde erstmals von Käsweber und Hänsch
[43] beschritten. Das so erhaltene Modell bietet die
Möglichkeit,
ein physikalisch motiviertes Transportmodell für Zweibandhalbleiter
in einem Simulator, der auf dem (erweiterten) Drift-Diffusionsmodell
für ein einziges Band basiert, ohne weitere Änderungen einzusetzen.
Man geht dabei wieder vom Gleichungssatz (3.23) - (3.28) aus
Kap. 3.1.1 aus, der für zwei Bänder getrennt angeschrieben wird.
Hier werden die beiden Bänder als  - und L-Band bezeichnet, da diese die
zwei tiefsten Minima in der Bandstruktur sind. Das so bezeichnete L-Band
repräsentiert jedoch auch den Einfluß höherenergetischer Bänder, wie den
des X-Bandes, was durch eine entsprechende Wahl der effektiven Masse erreicht
werden kann.
- und L-Band bezeichnet, da diese die
zwei tiefsten Minima in der Bandstruktur sind. Das so bezeichnete L-Band
repräsentiert jedoch auch den Einfluß höherenergetischer Bänder, wie den
des X-Bandes, was durch eine entsprechende Wahl der effektiven Masse erreicht
werden kann.
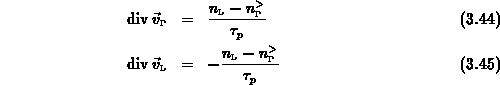
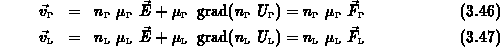
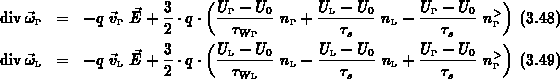
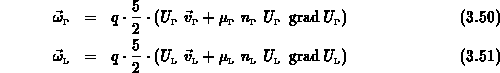
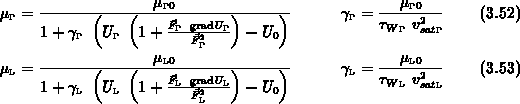
Größen mit Index  oder
oder  beziehen sich im folgenden immer auf das
jeweilige Band. Die neue Größe
beziehen sich im folgenden immer auf das
jeweilige Band. Die neue Größe 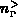 bezeichnet die Anzahl jener Elektronen
im
bezeichnet die Anzahl jener Elektronen
im  -Band, die eine Energie größer als der Abstand
-Band, die eine Energie größer als der Abstand 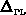 zwischen
zwischen  - und L-Band besitzen (Abb. 3.1).
Die Zeitkonstanten
- und L-Band besitzen (Abb. 3.1).
Die Zeitkonstanten 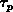 und
und 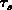 beschreiben
den Teilchen- und Energietransfer zwischen den Bändern.
beschreiben
den Teilchen- und Energietransfer zwischen den Bändern.
Ziel der weiteren Vorgangsweise ist es, eine Formulierung für die effektive
Beweglichkeit 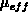 und die effektive Temperaturspannung
und die effektive Temperaturspannung 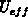 zu
finden, die in einer einzigen Transportgleichung verwendet werden kann.
zu
finden, die in einer einzigen Transportgleichung verwendet werden kann.
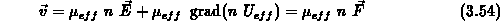
Die Gesamtteilchenzahl  , die gesamte Teilchenstromdichte
, die gesamte Teilchenstromdichte 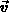 und die
gesamte Energiestromdichte
und die
gesamte Energiestromdichte 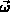 erhält man durch Addition der Größen
aus beiden Bändern.
erhält man durch Addition der Größen
aus beiden Bändern.
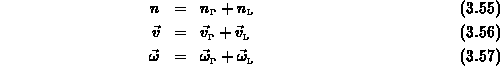
Unter der grundlegenden Annahme, daß auf die Teilchen in beiden Bändern
dieselbe Kraft 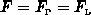 wirkt, erhält man aus (3.54)
und (3.56)
wirkt, erhält man aus (3.54)
und (3.56)
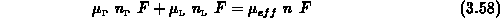
und damit die effektive Beweglichkeit
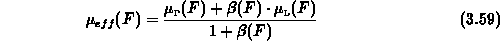
wobei 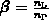 das Verhältnis zwischen den Anzahlen der Teilchen
im L-Band und der Teilchen in
das Verhältnis zwischen den Anzahlen der Teilchen
im L-Band und der Teilchen in  -Band beschreibt. Ebenso erhält man aus
(3.57) unter Vernachlässigung der räumlichen Ableitung der
Temperaturspannungen mithilfe von (3.48) und (3.50) die
effektive Temperaturspannung
-Band beschreibt. Ebenso erhält man aus
(3.57) unter Vernachlässigung der räumlichen Ableitung der
Temperaturspannungen mithilfe von (3.48) und (3.50) die
effektive Temperaturspannung
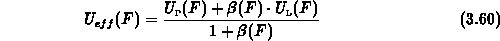
Der Zusammenhang zwischen 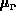 bzw.
bzw. 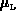 und
und 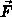 läßt sich in der in
Kap. 3.1.2 beschriebenen Weise herleiten.
läßt sich in der in
Kap. 3.1.2 beschriebenen Weise herleiten.
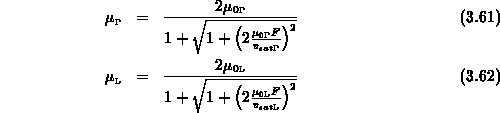
Dabei erhält man auch die Temperaturspannungen 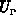 und
und 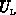 .
.
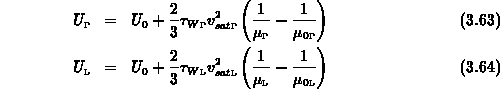
Die Gleichungen (3.61) - (3.64) enthalten sechs Parameter,
die Beweglichkeiten für schwaches Feld 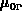 ,
, 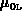 , die
Energierelaxationszeiten
, die
Energierelaxationszeiten 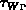 ,
, 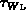 und die
Sättigungsgeschwindigkeiten
und die
Sättigungsgeschwindigkeiten 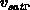 und
und 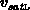 . Von diesen sechs
Parametern sind aber nur drei direkt experimentell zugänglich.
Die Beweglichkeit
. Von diesen sechs
Parametern sind aber nur drei direkt experimentell zugänglich.
Die Beweglichkeit 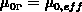 erhält man aus Messungen im schwachen
Feld, die Beweglichkeit
erhält man aus Messungen im schwachen
Feld, die Beweglichkeit 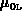 läßt sich aus Messungen bei niedrigen
Frequenzen bestimmen [7]. Die Energierelaxationszeit
läßt sich aus Messungen bei niedrigen
Frequenzen bestimmen [7]. Die Energierelaxationszeit 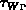 kann
man aus der Krümmung der Feldabhängigkeit der mittleren Energie für
kann
man aus der Krümmung der Feldabhängigkeit der mittleren Energie für
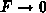 berechnen. Um die drei fehlenden Parameter
berechnen. Um die drei fehlenden Parameter 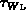 ,
,
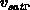 und
und 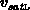 auf meßbare Größen zurückführen zu können,
benützt man die bisher noch nicht verwendeten Energieerhaltungsgleichungen
(3.48). Kombiniert man (3.48) und (3.50), so erhält
man unter den gleichen Voraussetzungen wie in Kap. 3.1.2 mit den
Abkürzungen
auf meßbare Größen zurückführen zu können,
benützt man die bisher noch nicht verwendeten Energieerhaltungsgleichungen
(3.48). Kombiniert man (3.48) und (3.50), so erhält
man unter den gleichen Voraussetzungen wie in Kap. 3.1.2 mit den
Abkürzungen 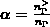 und
und 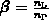
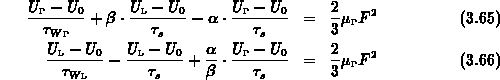
Betrachtet man (3.65) und (3.66) im Bereich für
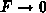 , wo
, wo
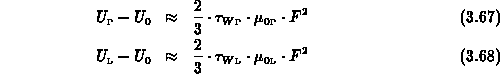
gilt, erhält man für die Energierelaxationszeiten
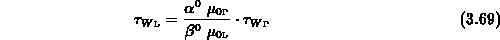
Kennt man nun die Teilchenverhältnisse im thermischen Gleichgewicht
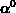 und
und 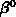 so kann man
so kann man 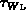 auf
auf 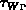 zurückführen.
zurückführen.
Für 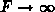 gilt
gilt
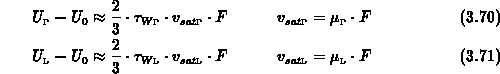
und man erhält für die Sättigungsgeschwindigkeiten mit (3.69)
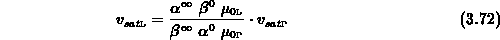
Mithilfe von (3.59) kann man die
Sättigungsgeschwindigkeiten 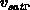 und
und 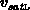 auf die experimentell
zugängliche Sättigungsgeschwindigkeit
auf die experimentell
zugängliche Sättigungsgeschwindigkeit 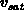 zurückführen.
zurückführen.
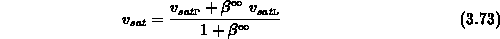
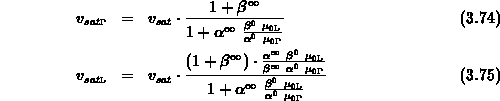
Als letzter Schritt in der Herleitung des erweiterten Transportmodells bleibt
jetzt noch die Bestimmung der Feldabhängigkeit der Teilchenverhältnisse
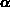 und
und 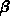 . Der Teilchentransfer (Abb. 3.1) wird durch
folgende Ratengleichungen beschrieben:
. Der Teilchentransfer (Abb. 3.1) wird durch
folgende Ratengleichungen beschrieben:
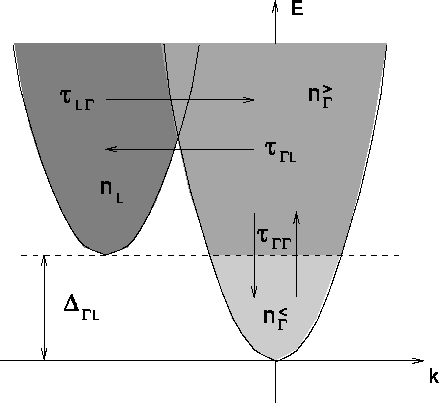
Abbildung 3.1: Teilchentransfer zwischen  - und L-Band
- und L-Band
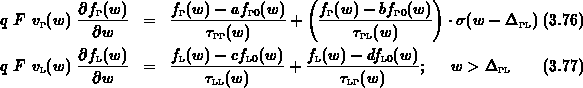
Die Änderung der Verteilungsfunktionen 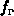 und
und 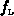 in Abhängigkeit
von der Bandenergie
in Abhängigkeit
von der Bandenergie  wird hier durch vier energieabhängige Streuzeiten
beschrieben, wobei
wird hier durch vier energieabhängige Streuzeiten
beschrieben, wobei 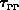 und
und 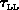 Übergänge innerhalb
der Bänder,
Übergänge innerhalb
der Bänder, 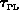 und
und 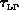 dagegen Übergänge zwischen den
Bändern angeben. Die Koeffizienten
dagegen Übergänge zwischen den
Bändern angeben. Die Koeffizienten  ,
, 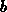 ,
,  und
und 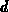 sind
energieunabhängig. Durch die Sprungfunktion
sind
energieunabhängig. Durch die Sprungfunktion 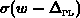 wird
berücksichtigt, daß Übergänge zwischen den Bändern erst bei einer Energie
größer als
wird
berücksichtigt, daß Übergänge zwischen den Bändern erst bei einer Energie
größer als 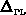 erfolgen können.
erfolgen können. 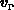 und
und 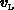 sind die
energieabhängigen mikroskopischen Teilchengeschwindigkeiten.
sind die
energieabhängigen mikroskopischen Teilchengeschwindigkeiten.
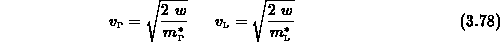
Normiert man die Energie auf 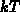 , erhält man mit den Abkürzungen
, erhält man mit den Abkürzungen
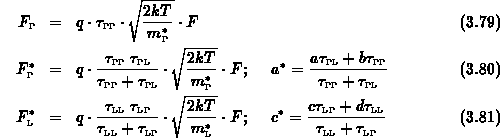
aus (3.76) und (3.77)
drei partielle Differentialgleichungen für die Verteilungsfunktionen
in den beiden Bändern.
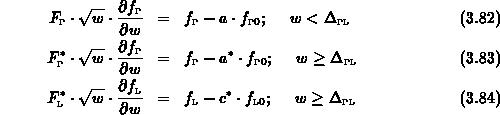
Im thermischen Gleichgewicht soll die Boltzmannstatistik gelten, d.h. für die
Verteilungsfunktionen 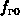 und
und 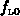 gilt
gilt
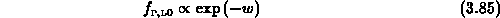
wobei  die normierte Energie bezeichnet.
Mit dieser Annahme erhalten wir drei inhomogene lineare Differentialgleichungen
der Form
die normierte Energie bezeichnet.
Mit dieser Annahme erhalten wir drei inhomogene lineare Differentialgleichungen
der Form
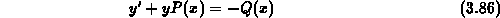
Die allgemeine Lösung dieser Differentialgleichung lautet
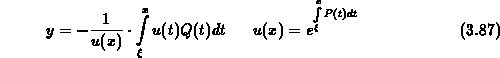
Die Lösung der Gleichungen (3.82) - (3.84) lautet nun:
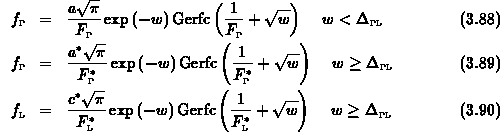
mit der Definition
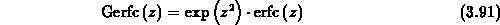
wobei 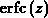 die komplementäre Fehlerfunktion bezeichnet.
Die Teilchendichten erhält man durch Integration des Produkts aus
Zustandsdichte und Verteilungsfunktion. Die Zustandsdichte in der Nähe der
Bandkante ist proportional zu
die komplementäre Fehlerfunktion bezeichnet.
Die Teilchendichten erhält man durch Integration des Produkts aus
Zustandsdichte und Verteilungsfunktion. Die Zustandsdichte in der Nähe der
Bandkante ist proportional zu 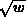 .
.
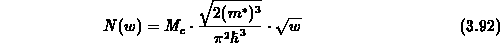
Integriert man (3.82) für 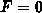 so erhält man für
so erhält man für 
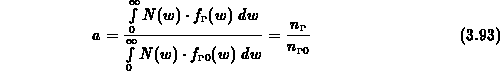
Ebenso erhält man aus (3.84)
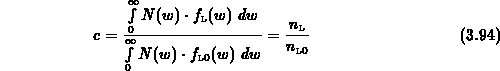
Die Integration von (3.88)-(3.90) liefert mithilfe der
Gammafunktion mit dem Argument 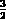
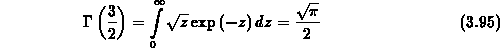
die detaillierten Teilchenzahlen im  - und L-Band
- und L-Band
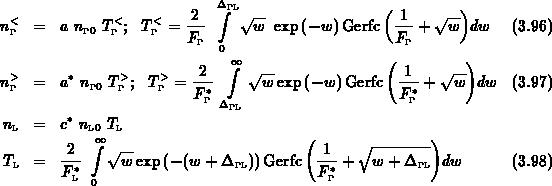
Die Transferintegrale 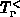 ,
, 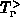 und
und 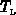 enthalten nun die
Feldabhängigkeit der Besetzungszahlen in den einzelnen Bändern. Damit ist es
jetzt möglich, die Feldabhängigkeit der Teilchenverhältnisse
enthalten nun die
Feldabhängigkeit der Besetzungszahlen in den einzelnen Bändern. Damit ist es
jetzt möglich, die Feldabhängigkeit der Teilchenverhältnisse 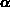 und
und
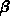 zu berechnen. Aus den Forderungen für Teilchenerhaltung im
zu berechnen. Aus den Forderungen für Teilchenerhaltung im
 -Band
-Band
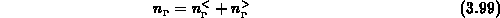
und der Teilchenerhaltung des Streuprozesses zwischen  - und L-Band
- und L-Band
(vgl. Abb. 3.1: alle aus dem  -Band hinausgestreuten Teilchen
müssen im L-Band ankommen und umgekehrt)
-Band hinausgestreuten Teilchen
müssen im L-Band ankommen und umgekehrt)
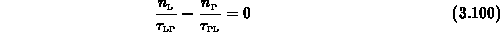
erhält man mit (3.93) und (3.94) für die
Teilchenverhältnisse
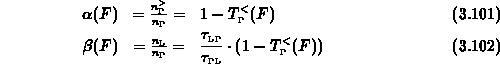
Mit (3.96), (3.102) und (3.59) - (3.64)
läßt sich die Feldabhängigkeit der effektiven Beweglichkeit 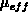 und
der effektiven Temperaturspannung
und
der effektiven Temperaturspannung 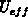 konsistent beschreiben. Neben den
meßbaren physikalischen Größen
konsistent beschreiben. Neben den
meßbaren physikalischen Größen 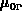 ,
, 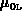 ,
, 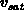 und
und
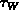 enthält das Modell die noch unbekannten Transferzeitkonstanten
enthält das Modell die noch unbekannten Transferzeitkonstanten
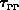 ,
, 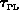 und
und 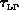 . Darüberhinaus
müssen noch die Grenzwerte der Teilchenverhältnisse für schwaches und
starkes Feld berechnet werden, um die fehlenden Parameter
. Darüberhinaus
müssen noch die Grenzwerte der Teilchenverhältnisse für schwaches und
starkes Feld berechnet werden, um die fehlenden Parameter 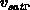 ,
,
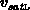 und
und 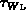 bestimmen zu können.
bestimmen zu können.
Die Abhängigkeit der Transferzeitkonstanten 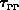 ,
, 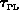 und
und
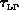 von der Bandenergie
von der Bandenergie  wurde in [14] berechnet. Sie wird hauptsächlich durch die Streuung an
polar optischen Phononen (Energie
wurde in [14] berechnet. Sie wird hauptsächlich durch die Streuung an
polar optischen Phononen (Energie 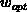 ) bestimmt.
) bestimmt.
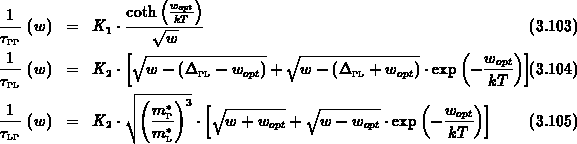
Um daraus einen geeigneten Mittelwert zu berechnen, wird eine mit der jeweiligen
Elektronentemperatur skalierte Boltzmann-ähnliche Verteilung
(3.106) verwendet.
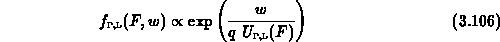
Nach Durchführung der Mittelwertbildung erhält man unter
den Voraussetzungen
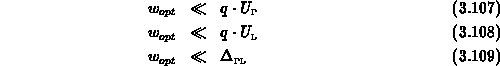
mithilfe der Definition der unvollständigen Gammafunktion
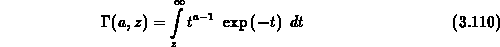
folgende Abhängigkeiten für die Transferzeiten:
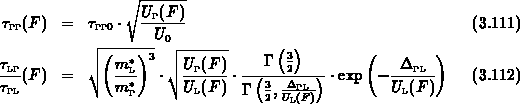
Damit bleibt als letzter Schritt zur Vervollständigung des Modells
nur mehr die Berechnung der Teilchenverhältnisse 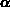 und
und 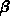 in den Grenzwerten für starkes und schwaches Feld.
Für starkes Feld erhält man für
in den Grenzwerten für starkes und schwaches Feld.
Für starkes Feld erhält man für 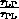
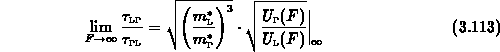
Mit (3.67) - (3.72) erhält man
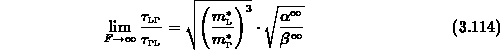
daraus mit (3.101), (3.102) und 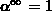
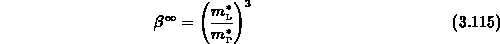
Im Grenzwert 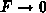 gilt
gilt
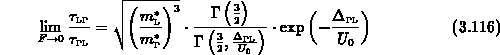
Damit erhält man das Verhältnis
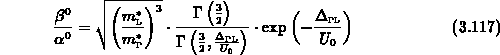
Die Beschreibung des Elektronentransports im Zweibandsystem ist nun komplett und
enthält neben den meßbaren Parametern 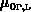 ,
, 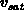 und
und
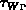 nur einen einzigen Fitparameter, nämlich die Transferzeit für
Übergänge im
nur einen einzigen Fitparameter, nämlich die Transferzeit für
Übergänge im  -Band
-Band 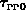 . Der Wert für
. Der Wert für 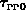 liegt
in der Größenordnung von
liegt
in der Größenordnung von 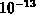 Sekunden und bestimmt jenen Wert der
treibenden Kraft, für den merkliche Streuung der
Sekunden und bestimmt jenen Wert der
treibenden Kraft, für den merkliche Streuung der  -Elektronen in das
L-Band auftritt.
-Elektronen in das
L-Band auftritt.
Zu bemerken ist, daß in dieser Beschreibung die Transportparameter 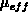 und
und 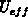 lokal von der treibenden Kraft abhängen. Nichtlokale Effekte
können also mit diesem Modell nicht beschrieben werden. Details zur
Implementierung und die numerische Auswertung und Überprüfung dieses Modells
werden in Kap. 3.4.3 beschrieben.
lokal von der treibenden Kraft abhängen. Nichtlokale Effekte
können also mit diesem Modell nicht beschrieben werden. Details zur
Implementierung und die numerische Auswertung und Überprüfung dieses Modells
werden in Kap. 3.4.3 beschrieben.




Next: 3.2 Der Schottkykontakt
Up: 3.1 Die Halbleitergleichungen
Previous: 3.1.3 Einbeziehung nichtlokaler Effekte
Martin Stiftinger
Fri Oct 14 19:00:51 MET 1994
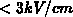 ) zulässig. Eine Betrachtung der Bandstruktur
(Abb. 3.10) legt jedoch nahe, den Elektronentransport mithilfe
eines Zweibandmodells zu beschreiben (siehe Kap. 3.4.1). Das würde
aber bedeuten, beide Bänder getrennt zu behandeln und für jedes
Band eine eigene Transport- und Erhaltungsgleichung zusammen mit
der Poissongleichung zu lösen. Dazu käme im einfachsten Fall noch eine
Beschreibung des Teilchentransfers zwischen den beiden Bändern.
Allerdings erfordert diese Methode beträchtlichen Mehraufwand bei der
numerischen Lösung des resultierenden Gleichungssystems, und eine effiziente
Implementierung in einen bestehenden Simulator, der auf der
Drift-Diffusionsnäherung basiert, ist nur schwer möglich.
) zulässig. Eine Betrachtung der Bandstruktur
(Abb. 3.10) legt jedoch nahe, den Elektronentransport mithilfe
eines Zweibandmodells zu beschreiben (siehe Kap. 3.4.1). Das würde
aber bedeuten, beide Bänder getrennt zu behandeln und für jedes
Band eine eigene Transport- und Erhaltungsgleichung zusammen mit
der Poissongleichung zu lösen. Dazu käme im einfachsten Fall noch eine
Beschreibung des Teilchentransfers zwischen den beiden Bändern.
Allerdings erfordert diese Methode beträchtlichen Mehraufwand bei der
numerischen Lösung des resultierenden Gleichungssystems, und eine effiziente
Implementierung in einen bestehenden Simulator, der auf der
Drift-Diffusionsnäherung basiert, ist nur schwer möglich.




 - und L-Band bezeichnet, da diese die
zwei tiefsten Minima in der Bandstruktur sind. Das so bezeichnete L-Band
repräsentiert jedoch auch den Einfluß höherenergetischer Bänder, wie den
des X-Bandes, was durch eine entsprechende Wahl der effektiven Masse erreicht
werden kann.
- und L-Band bezeichnet, da diese die
zwei tiefsten Minima in der Bandstruktur sind. Das so bezeichnete L-Band
repräsentiert jedoch auch den Einfluß höherenergetischer Bänder, wie den
des X-Bandes, was durch eine entsprechende Wahl der effektiven Masse erreicht
werden kann.
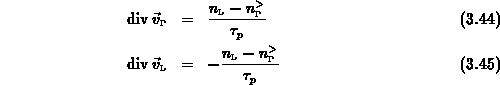
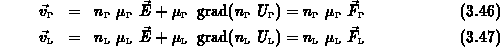
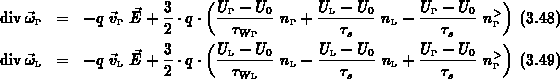
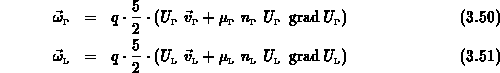
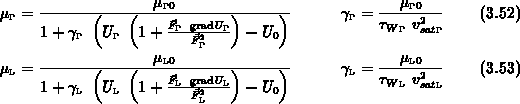
 oder
oder  beziehen sich im folgenden immer auf das
jeweilige Band. Die neue Größe
beziehen sich im folgenden immer auf das
jeweilige Band. Die neue Größe 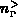 bezeichnet die Anzahl jener Elektronen
im
bezeichnet die Anzahl jener Elektronen
im 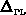 zwischen
zwischen 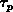 und
und 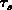 beschreiben
den Teilchen- und Energietransfer zwischen den Bändern.
beschreiben
den Teilchen- und Energietransfer zwischen den Bändern.
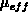 und die effektive Temperaturspannung
und die effektive Temperaturspannung 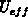 zu
finden, die in einer einzigen Transportgleichung verwendet werden kann.
zu
finden, die in einer einzigen Transportgleichung verwendet werden kann.
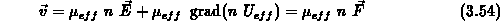
 , die gesamte Teilchenstromdichte
, die gesamte Teilchenstromdichte 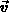 und die
gesamte Energiestromdichte
und die
gesamte Energiestromdichte 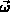 erhält man durch Addition der Größen
aus beiden Bändern.
erhält man durch Addition der Größen
aus beiden Bändern.
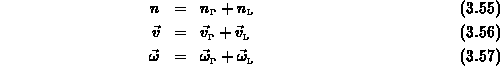
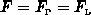 wirkt, erhält man aus (
wirkt, erhält man aus (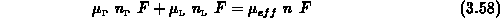
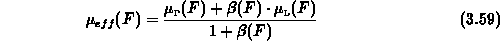
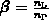 das Verhältnis zwischen den Anzahlen der Teilchen
im L-Band und der Teilchen in
das Verhältnis zwischen den Anzahlen der Teilchen
im L-Band und der Teilchen in 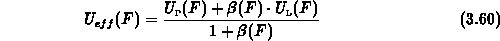
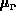 bzw.
bzw. 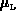 und
und 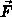 läßt sich in der in
Kap.
läßt sich in der in
Kap. 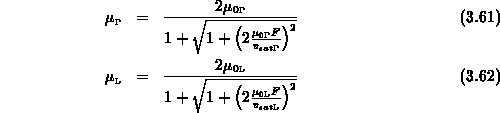
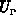 und
und 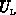 .
.
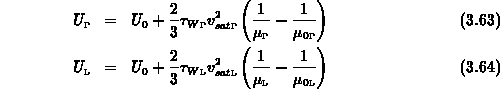
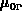 ,
, 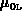 , die
Energierelaxationszeiten
, die
Energierelaxationszeiten 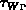 ,
, 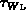 und die
Sättigungsgeschwindigkeiten
und die
Sättigungsgeschwindigkeiten 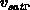 und
und 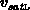 . Von diesen sechs
Parametern sind aber nur drei direkt experimentell zugänglich.
Die Beweglichkeit
. Von diesen sechs
Parametern sind aber nur drei direkt experimentell zugänglich.
Die Beweglichkeit 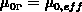 erhält man aus Messungen im schwachen
Feld, die Beweglichkeit
erhält man aus Messungen im schwachen
Feld, die Beweglichkeit 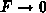 berechnen. Um die drei fehlenden Parameter
berechnen. Um die drei fehlenden Parameter 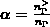 und
und 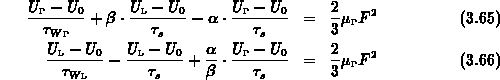
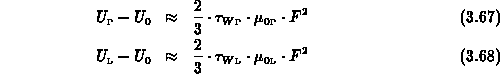
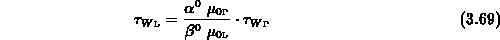
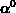 und
und 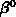 so kann man
so kann man 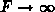 gilt
gilt
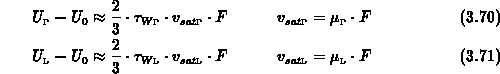
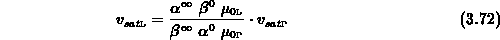
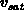 zurückführen.
zurückführen.
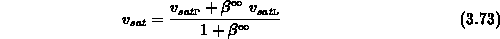
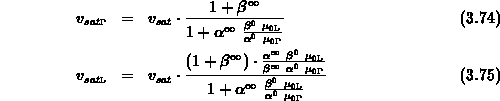
 und
und  . Der Teilchentransfer (Abb.
. Der Teilchentransfer (Abb. 
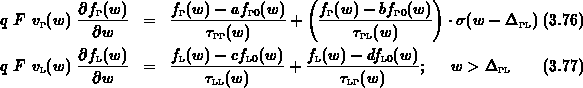
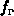 und
und 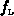 in Abhängigkeit
von der Bandenergie
in Abhängigkeit
von der Bandenergie  wird hier durch vier energieabhängige Streuzeiten
beschrieben, wobei
wird hier durch vier energieabhängige Streuzeiten
beschrieben, wobei 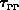 und
und 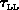 Übergänge innerhalb
der Bänder,
Übergänge innerhalb
der Bänder, 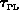 und
und 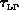 dagegen Übergänge zwischen den
Bändern angeben. Die Koeffizienten
dagegen Übergänge zwischen den
Bändern angeben. Die Koeffizienten  ,
, 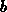 ,
,  und
und 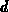 sind
energieunabhängig. Durch die Sprungfunktion
sind
energieunabhängig. Durch die Sprungfunktion 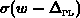 wird
berücksichtigt, daß Übergänge zwischen den Bändern erst bei einer Energie
größer als
wird
berücksichtigt, daß Übergänge zwischen den Bändern erst bei einer Energie
größer als 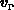 und
und 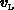 sind die
energieabhängigen mikroskopischen Teilchengeschwindigkeiten.
sind die
energieabhängigen mikroskopischen Teilchengeschwindigkeiten.
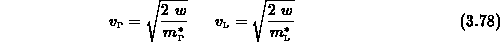
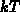 , erhält man mit den Abkürzungen
, erhält man mit den Abkürzungen
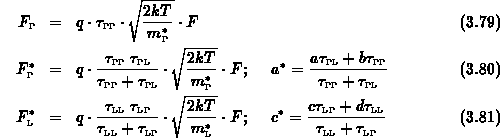
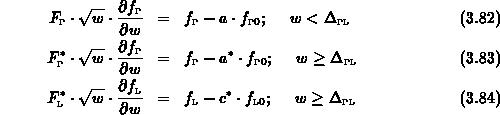
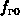 und
und 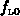 gilt
gilt
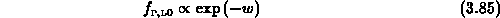
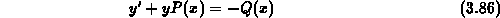
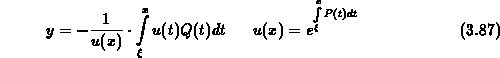
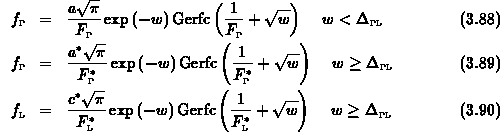
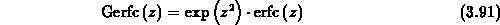
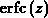 die komplementäre Fehlerfunktion bezeichnet.
Die Teilchendichten erhält man durch Integration des Produkts aus
Zustandsdichte und Verteilungsfunktion. Die Zustandsdichte in der Nähe der
Bandkante ist proportional zu
die komplementäre Fehlerfunktion bezeichnet.
Die Teilchendichten erhält man durch Integration des Produkts aus
Zustandsdichte und Verteilungsfunktion. Die Zustandsdichte in der Nähe der
Bandkante ist proportional zu 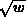 .
.
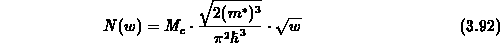
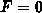 so erhält man für
so erhält man für 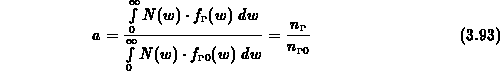
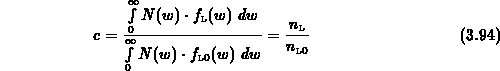
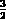
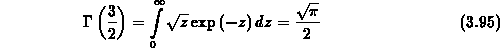
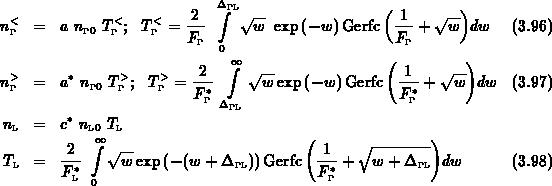
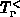 ,
, 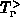 und
und 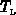 enthalten nun die
Feldabhängigkeit der Besetzungszahlen in den einzelnen Bändern. Damit ist es
jetzt möglich, die Feldabhängigkeit der Teilchenverhältnisse
enthalten nun die
Feldabhängigkeit der Besetzungszahlen in den einzelnen Bändern. Damit ist es
jetzt möglich, die Feldabhängigkeit der Teilchenverhältnisse 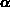 und
und
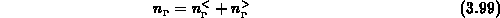
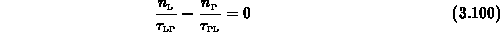
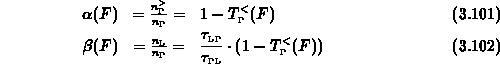
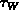 enthält das Modell die noch unbekannten Transferzeitkonstanten
enthält das Modell die noch unbekannten Transferzeitkonstanten
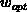 ) bestimmt.
) bestimmt.
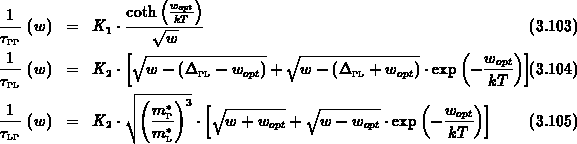
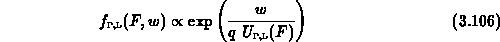
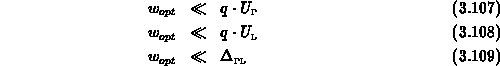
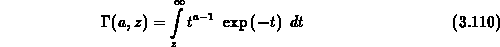
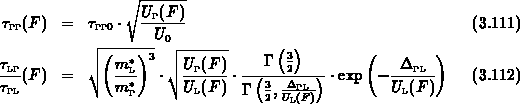
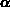 und
und 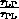
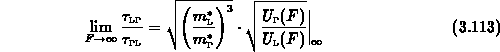
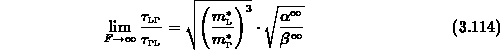
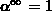
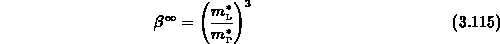
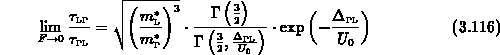
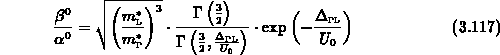
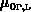 ,
, 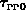 . Der Wert für
. Der Wert für 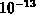 Sekunden und bestimmt jenen Wert der
treibenden Kraft, für den merkliche Streuung der
Sekunden und bestimmt jenen Wert der
treibenden Kraft, für den merkliche Streuung der