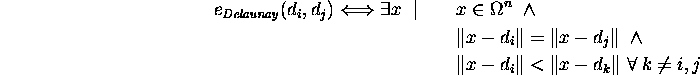
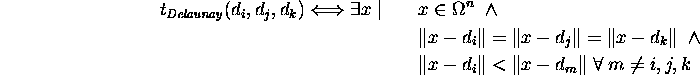
Some modifications of the surface of the three-dimensional structure are required prior to the actual meshing procedure. The volume decomposition performed by the tetrahedrization module uses a modified advancing front algorithm. The adapted surface of the geometry provides the initial front. The Constrained Delaunay triangulation which would allow the embedding of an unaltered surface into the Delaunay tetrahedrization is not yet well defined in three dimensions and remains an open problem. In one way or the other it becomes necessary to transform the surface to be contained in a Conforming Delaunay tetrahedrization: A non-planar Delaunay surface triangulation of the geometry is generated which will be part of a geometry conform Delaunay mesh. It provides the core meshing algorithm with the initial front. A general polygonal description of the boundaries and interfaces is read as well as an optional set of grid nodes to be reused. The applied Delaunay criterion for a surface triangle is based on the following two properties (Fig. 2):
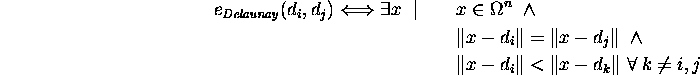
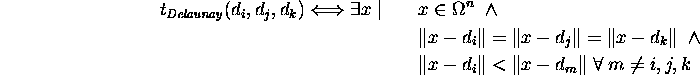
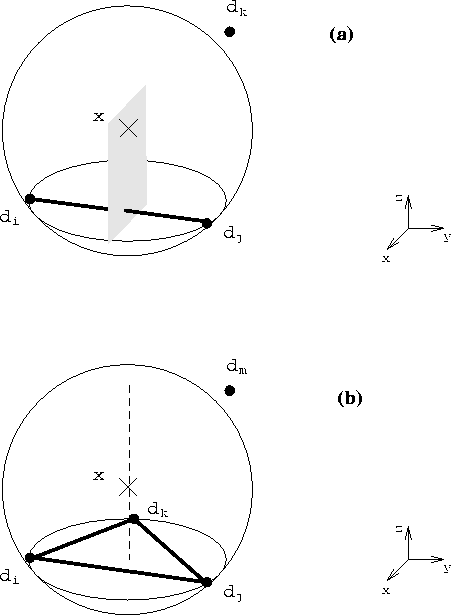
Figure 2: The Delaunay edge (a) and Delaunay triangle (b) property.
A fast point location method becomes crucial for the verification of this criterion. We implemented a point bucket octree to store all grid nodes at all times. The following steps are involved to adapt the given surface for use with the tetrahedrization algorithm and to derive a three-dimensional Delaunay surface triangulation.
Figure 3: MOS Transistor as polygonal input.
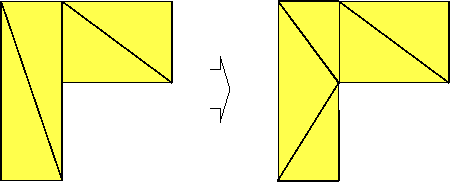
Figure 4: Edge splitting can be a necessary conversion of the input data to yield a well connected surface triangulation.
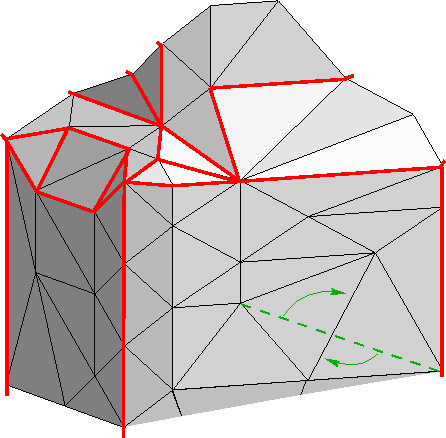
Figure 5: Non-flippable feature edges are drawn in a red color. The green edge is an example of a local transformation.
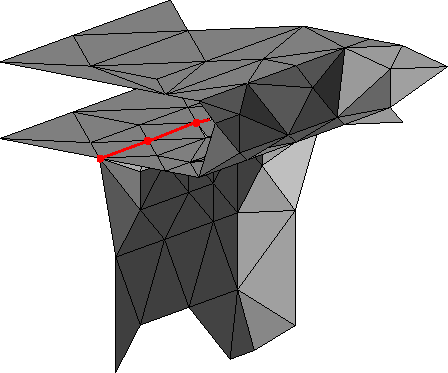
Figure 6: An example of a ``triple line''.
Note, that in the worst case these heuristics may fail to produce a surface representation compliant with the above stated properties. In such a case a few non-delaunay triangles exist which require a special handling during the tetrahedrization process (See robustness issues at the end of the next section.) The underlying goal of the surface modeling procedure is to automatically understand complex three-dimensional structures. The generated Delaunay surface representation (Fig. 7) is fed into the modified advancing front algorithm.
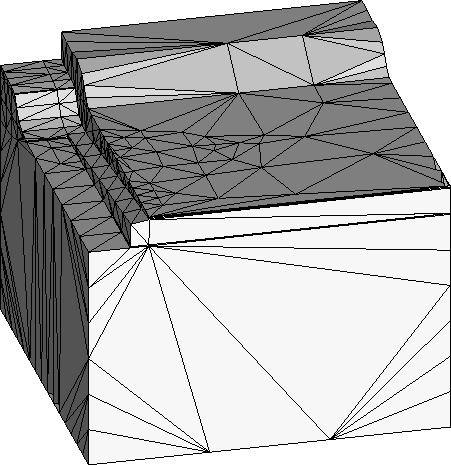
Figure 7: Delaunay surface triangulation