The generated Delaunay triangles representing the boundaries and interfaces form an oriented initial front. These triangles can be imagined as seeds which are inserted into a queue to ``grow'' tetrahedra. At the start, the algorithm needs a non-empty queue. It does not require the queue to hold all surface triangles. One triangle per enclosed segment is sufficient. The surface triangulation has two purposes:
In the described manner a segment of the input domain is ``filled'' with tetrahedra, if there exists at least one seed triangle which has a normal vector that points into the volume of the segment. Another way of imagining the meshing process is to substitute the tetrahedra with ``water'' and the closed boundary with a watertight container. At the location of the seed triangles water will be poured into the container. The surface of the water as it fills the container is the advancing front.
The following questions arise:
What degree of freedom does the algorithm have to choose a tetrahedron to be attached to a triangle of the queue ? What kind of tetrahedron will be chosen ?
How is it guaranteed that the advancing front does not pass through itself or the given boundary triangulation ? (How is it guaranteed that ``water does not spill outside of the container'' ?)
How is it guaranteed that no part of the domain remains untetrahedrized ?
First, consider that during the time instance when a triangle is taken from the queue and processed (it will be called the current ``base triangle'') the grid node placement is known and fixed. (Grid nodes can have several origins: They can partly be input to force certain nodes into the mesh and/or be generated through a quality improvement loop discussed in Section 4.) This is an important modification to general advancing front methods. Second, consider that for a fixed point set the Delaunay triangulation is well defined. To see the answers to the above questions let us first assume that the Delaunay triangulation is unique. Given a fixed grid node distribution and an oriented triangle only one grid node can complement the triangle to form a valid Delaunay tetrahedron to be attached to the triangle's front side. The meshing algorithm will choose to create exactly this tetrahedron. It is intrinsically not able to create any non-delaunay tetrahedra ! Below will be explained in detail how the fourth vertex which forms the only possible correct Delaunay tetrahedron is determined. To answer the second question we will show that a triangle existence test is sufficient to avoid cases where the advancing front generates loops or passes through borders. Such a test whether or not an identical triangle already exists is easy to implement and does not cost performance.
Also, the triangle existence test guarantees that the algorithm terminates. Since no Delaunay triangles are generated more than once and the overall number of Delaunay triangles t in a Delaunay triangulation is finite, the algorithm terminates after at most t steps. The answer to the third question is straightforward.
In Fig. 8 the current base triangles at each step are shaded.
Figure 8: Modified advancing front method.
We will now describe how the fourth vertex is determined which
completes the given base triangle to yield a Delaunay tetrahedron.
(Remember that due to the surface treatment and the way the advancing
front is built all triangles and hence all base triangle always
satisfy the Delaunay triangle
property.)
A local region around the base triangle is examined to find the correct
fourth point. The border of this region is defined by a sphere
containing the circumcircle of the base triangle. The radius of the
sphere will be increased as long as the sphere does not contain other
points. For an easier understanding you may imagine the circumcircle
of the base triangle to be a ring which was dipped in soap water and
the sphere to be the soap bubble which is blown up.
That one sphere must exist which does not hold any other
points is evident due to the Delaunay property of the
base triangle. In fact, the way the region around the base triangle
is examined closely resembles the Delaunay property.
The size of the sphere is increased so that exactly one other
point (than the three points of the base triangle) is located on the
perimeter of the sphere. This point is the seeked fourth vertex of the
tetrahedron. It is evident that the tetrahedron must satisfy the
Delaunay property, because its circumsphere does not contain any other
point. For one base triangle two spheres exist
that correspond to a tetrahedron on each side. The algorithm will
only attach a tetrahedron to the front side of the base triangle as
previously explained. It will therefore increase the size of the
sphere in this manner that the positive normal distance 
between the
center M of
the sphere and the base triangle is increased. The normal distance
can be negative (H denotes the circumcenter of the base triangle and
its unit length normal vector.):
The time complexity of the algorithm depends heavily on the point location method. We implemented a fast point bucket octree which provides us with a recursive search function for arbitrary rectangular search regions parallel to the bounding box. Fig. 9 shows the two-dimensional analogy.
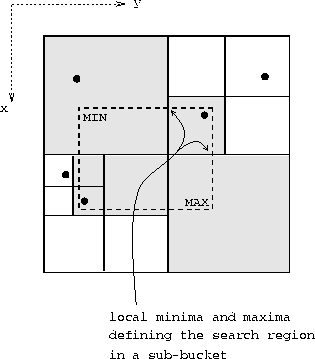
Figure 9: Point location within a given
search region.
The sphere defining the search region always fits into a cube which is
parallel to the bounding box. The gradual increase of the size of the
search region does not cost extra performance: If the sphere is too
small no points will be located inside the search region and the
effort of traversing the octree is minimal. The case when exactly one
point (the fourth vertex of the tetrahedron) is found is
ideal. Usually, The search region will contain several points. In such
a case the size of the sphere defining the search region will not be
reduced until only a single point is contained. Instead, 
will be computed from 
which is the center of the sphere defined by the
point 
and the base triangle. The point 
with minimal
is the correct fourth vertex of the tetrahedron.
The octree search and the minimizing of
(-criterion) introduces the logarithm into the overall time
complexity 
where n is the number of tetrahedra.
The scope of the possible values is numerically a delicate matter.
For a robust implementation additional geometric tests (like
an in-sphere-test) are required. Fig. 10 shows the
two-dimensional analogy: The normal distance of a point P to the
plane containing the base triangle (in two dimensions the ``base
edge'') is d . Fig. 10 shows a point 
with d = 0
and a point 
with a positive d (on the front side of the base
edge). Starting from the base edge the algorithm has to determine
which of the two points and is the correct point with
which to create a triangle (two-dimensional analogy). The correct
triangle is drawn with dashed lines. The various possible geometric locations
of a point are illustrated with their corresponding values.
The location of points with 
is denoted by the dashed
circle. The point is on a numerical critical location:
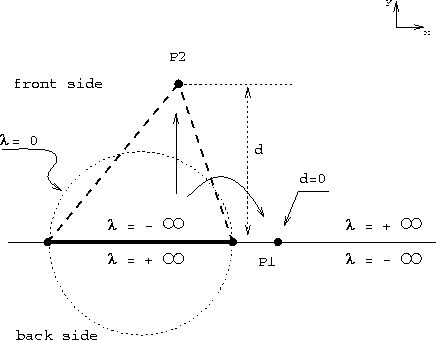
Figure 10: regions (2D analogy).
So far, we assumed that the Delaunay triangulation is unique. We remove this restriction to allow an arbitrary positioning of grid nodes. In a practical meshing application any restriction on the placement of grid nodes, e.g. to avoid degenerate Delaunay cases, would not be feasible. Therefore, we allow the occurrence of the following cases, which are very closely related to each other and represent the ambiguity of the Delaunay triangulation:
Note that cocircular point sets are more complex to deal with than
cospherical point sets. Indeed, a cocircular point set implies two
neighboring cospherical point sets !
Under exact arithmetics these cases result in a compound of points
with identical 
. We developed an approach
which takes both the topography as well as the at the moment existing
topology into account to avoid inconsistencies due to .
The robust implementation under finite precision arithmetics
detects these compounds and processes them separately as
an isolated triangulation sub-problem.
Starting with a base triangle a fourth point from the set of
cospherical points is chosen to generate a tetrahedron.
This first tetrahedron penetrating the sphere defined by the cospherical point
set forms a temporary convex boundary
to which the other points of are added one after another.
The temporary boundary is kept convex by ``looking back'' from each
fourth point of the last generated tetrahedron to link it to all
triangles with a positive minimum distance and thereby creating
several tetrahedra in one step.
Once the sphere is completely tetrahedrized, the ``looking back''
algorithm becomes unnecessary and it is returned to the normal
tetrahedra growth process. Note that ``looking back'' and checking the
minimum distance to the triangles is only required for triangles which
belong to the triangulation of the sphere. In fact, we use a temporary
second queue for the advancing front within the sphere. Therefore, we
have to examine only a very small number of triangles to determine
their minimum distance to the current fourth point.
A more detailed description of this algorithm can be found in
[2].
The cocircular point sets and the untetrahedrizable Delaunay polyhedron merit further discussion. Concerning the latter one should distinguish a general untetrahedrizable polyhedron (Schoenhardt polyhedron, twisted prism [4]) and an untetrahedrizable cavity formed by Delaunay triangles. The modified advancing front algorithm will not create or encounter the general non-Delaunay twisted prism case. This follows directly from the fact that the advancing front consists of Delaunay triangles only. Thus, such a case may only occur if the input structure forms a Schoenhardt polyhedron. It will be transformed or refined by the surface preprocessor, because the triangles do not fulfill the delaunay criterion. The question remains how to deal with the Delaunay twisted prism case. The points of such a cavity/polyhedron form a cospherical point set (Fig. 11).
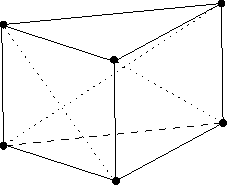
Figure 11: A surface triangulation of 6
cospherical points. If the upper three points which define a
circle are rotated (``twisted'') clockwise, an
untetrahedrizable polyhedron is formed.
If such a polyhedron evolves in the interior of the mesh during the tetrahedrization process, the surface of the polyhedron is not imperative. The algorithm is allowed to modify the Delaunay triangles that form the polyhedron in a local remeshing step. In Section 4 the interesting fact is shown that cocircular point sets, the untetrahedrizable Delaunay polyhedron, and a special type of sliver can all be treated in a similar way.
Furthermore, some general aspects are worthwhile to mention:
The growth process is restricted to the interior of a structure by its Delaunay boundary representation. The exterior domain will not be meshed and a segmentation (distinguishing interior elements from exterior elements and discarding the latter) is not necessary. In cases of extremely non-convex input geometries where the convex hull is much larger than the to be meshed domain a lot of computation time can be saved. For robustness issues assume that the Delaunay boundary representation is faulty: When the surface modeling procedure fails to produce a ``water tight'' Delaunay boundary representation, a few non-delaunay triangles exist (``leaks''). It is possible to check that the generated tetrahedra do not penetrate these surface triangles. In this way it can be avoided that tetrahedra are ``spilled'' into the exterior of the structure. It becomes necessary to calculate the intersection between these triangles and the currently generated tetrahedron during the growth process. This can be accomplished efficiently provided that the number of leaks is relatively small.
Complex structures and multiple connected domains will rigorously be ``filled'' with tetrahedra during the growth process.
A more flexible algorithm allows the meshing of boundaries which do not form a closed surface. This generalization is easily implemented. If no fourth vertex is found to attach a tetrahedron to a base triangle, the base triangle can be interpreted as part of the boundary. In this way boundary triangles are generated during the tetrahedrization process at local convex regions of the grid node distribution. (See also Fig. 13 and Fig. 17 as an example of an open surface representing the input geometry.)
Fig. 12 shows the performance for randomly distributed grid nodes on a workstation. The exact values are given below.
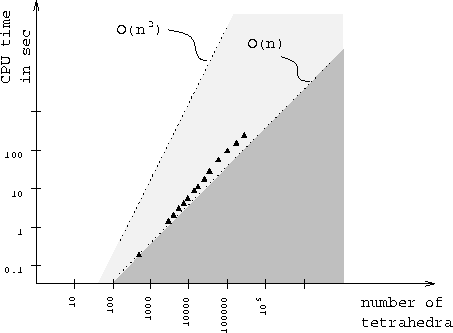
Figure 12: Performance on an HP 9000-735/100.
Finally, Fig. 1 shows snapshots of the advancing front during the meshing of a hand. Merely for demonstration purposes we meshed the region of one material after sputter deposition. The tetrahedra growth process is depicted in Fig. 13 and the mesh is shown in Fig. 17. The minimum of information is sufficient which is a boundary description of the non-convex part of the surface.
Figure 13: The tetrahedra growth process.