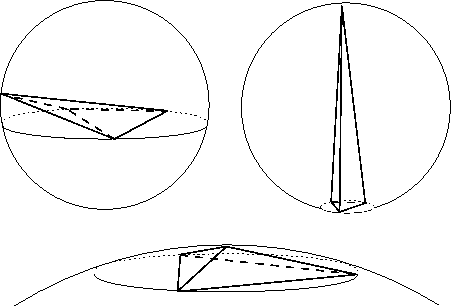
Figure 14: Elements with bad quality: sliver (upper left), needle (upper right), cap (bottom).
The grid node placement occurs during an iterative mesh improvement loop. It is also possible to force grid nodes into the mesh by providing the algorithm with a set of previously generated grid nodes. If an initial grid node distribution is desired, it is fairly easy to produce one. No restrictions on the location of grid nodes exist of any sort. They can be arbitrarily positioned and no care has to be taken that e.g. they are located interior of the structures. Starting with either no interior grid nodes or with a previously generated grid node distribution the initial mesh is constructed. The resulting elements will be too coarse. Also, a Delaunay tetrahedrization commonly contains elements with undesirable shape. Especially, for Finite Element Methods additional element quality measures become necessary to avoid such slivers, caps, or needles [4]. See Fig. 14.

Figure 14: Elements with bad quality: sliver (upper left), needle (upper right), cap (bottom).
Such general element quality measures, reflecting not only the shape of the elements but also the desired mesh density, can now be applied to the initial mesh. The basis for such adaptations is an efficient local regridding technique. This is straightforward due to the modified advancing front algorithm. The local removal of tetrahedra is the reverse process to the growth process. It results in a front surrounding the region to be regridded. The following steps are involved in this order:
Fig. 15 shows a two-dimensional example where the circumcenter of a triangle is inserted and local regridding is performed.
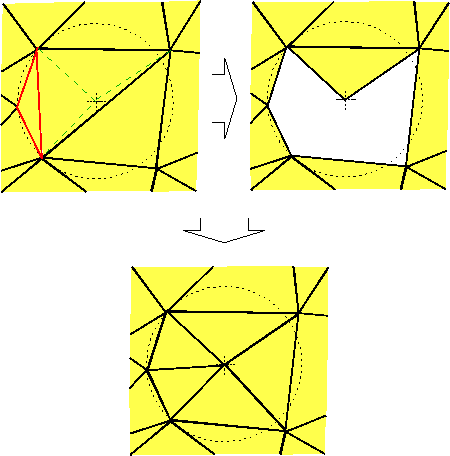
Figure 15: Steiner Point insertion for a bad element. The removal of non-delaunay elements (gap) is concluded by local regridding.
This local regridding technique can be utilized for several purposes:
At the moment, the following two criteria are implemented:
A special local refinement technique is used to improve the quality and/or to reduce the size of an element yielding the inner grid nodes. (See also Fig. 15.) A Steiner Point is inserted at the circumcenter of the circumsphere of the bad element, and the Delaunay property is restored by subsequent local regridding [1],[4]. The bad element is not necessarily refined itself (instead a neighboring element might be refined), but due to its destroyed Delaunay property (a point was inserted inside of its sphere) it must be improved during the subsequent Delaunay restoration step. The difference of a Delaunay triangulation compared to a Delaunay triangulation with Steiner Points can be seen in the two-dimensional example in Fig. 16. If the Steiner Point lies outside of the domain, it will not be inserted. If the bad element is located at the boundary, it will not be refined. If it is not located at the boundary, an element can be found that is located at the boundary and partly inside of the sphere of the bad element. This found element can be refined (e.g. its boundary face) ensuring that the inserted Steiner point is inside of the sphere of the bad element. This guarantees that the bad element will be modified in a subsequent Delaunay restoration step. This method may not succeed to improve angle criteria for elements at the boundary. Imagine two boundary edges that form an angle which does not fulfill an e.g. minimum angle criterion. There does not exist a refinement method to resolve the sharp angle.
Figure 16: Ordinary Delaunay triangulation vs. Delaunay triangulation with Steiner Points.
It has to be noted that this refinement method is suitable for
the removal of caps and needles in three dimensions. However, it has
difficulties with the removal of slivers [5]. This follows
from the fact that slivers do not exhibit extreme ratios between the
length of their edges.
Often such sliver tetrahedra (the four points are located close to the
equator of the circumsphere) are formed with four points from a subset of
![]() .
Such sliver elements can be treated in the same manner as cocircular point
sets and the untetrahedrizable Delaunay polyhedron (as already stated in
Section 3).
This rather interesting interpretation can be seen as follows:
.
Such sliver elements can be treated in the same manner as cocircular point
sets and the untetrahedrizable Delaunay polyhedron (as already stated in
Section 3).
This rather interesting interpretation can be seen as follows:
In all cases local transformations [3] to swap faces and their attached tetrahedra is the suggested method to remove these slivers. For the example of a sliver with a small positive volume the face swapping technique modifies the local connectivity between the neighboring elements in such a way that the sliver element can be removed without leaving a gap. The number of elements changes during face swapping from 3 to 2. However, it is only possible to apply such transformations for point sets that have an ambiguous Delaunay triangulation.
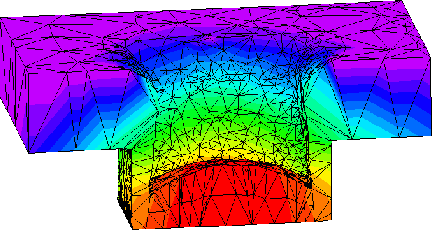
Figure 17: Mesh with 6558 elements after a single adaptation step.