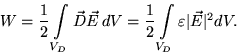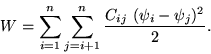
Next: APPLICATIONS AND RESULTS Up: No Title Previous: INTERFACING AND GEOMETRIC PROCESSING

MATHEMATICAL MODELS

For the numerical simulations we apply the finite element based package SAP [4,5]. For the partial capacitance extraction problem Laplace's equation

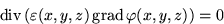$\begin{displaymath}\mathop{\mathrm{div}}\left(\varepsilon(x,y,z)\mathop{\mathrm{grad}}\varphi(x,y,z)\right)=0 \end{displaymath}$

((1)*main::open_tags)

is solved in the insulator domain V_D for various applied conductor voltages of the wiring structure to achieve the potential distribution 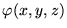$\varphi(x,y,z)$ .An equivalent formulation of this problem is the minimization of the functional

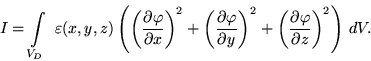$\begin{displaymath} I=\int\limits_{V_D}~\varepsilon(x,y,z)\left( \left({\frac{\p... ...left({\frac{\partial\varphi}{\partial z}}\right)^2\right)\,dV. \end{displaymath}$

((2)*main::open_tags)

For linear and isotropic dielectrica (2) represents exactly twice the electrostatic field energy

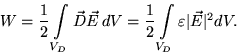$\begin{displaymath}W=\frac12\int\limits_{V_D}\vec D\vec E\,dV= \frac12\int\limits_{V_D}\varepsilon\vert\vec E\vert^2dV. \end{displaymath}$

((3)*main::open_tags)

The total electric field energy in a system of n conductors can be expressed as the sum of the energies stored in the 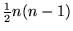$\frac12n(n-1)$ partial capacitances C_ij

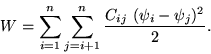$\begin{displaymath}W=\sum\limits_{i=1}^n\sum\limits_{j=i+1}^n\frac{C_{ij}~(\psi_i-\psi_j)^2}{2}. \end{displaymath}$

((4)*main::open_tags)

Therefore, the energy has to be calculated for 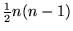$\frac12n(n-1)$ different conductor potential configurations. All partial capacitance values are obtained by solving the resulting linear system.

The temperature distribution, current density and non-linear resistances are obtained by a coupled electro-thermal simulation. Potential distribution and current density are calculated by solving the equation

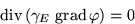$\begin{displaymath}\mathop{\mathrm{div}}\,(\gamma_E\,\mathop{\mathrm{grad}}\/\varphi)=0 \end{displaymath}$

((5)*main::open_tags)

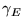in the conductor domains. $\gamma_E$ represents the electrical conductivity and is assumed to be 0 in all insulators. To obtain the temperature T profile the stationary heat conduction equation

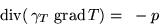$\begin{displaymath}\mathop{\mathrm{div}}(\,\gamma_T\,\mathop{\mathrm{grad}}\/T)=~ -p \end{displaymath}$

((6)*main::open_tags)

is solved in the whole simulation region. 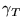$\gamma_T$ represents the thermal conductivity, and the term p on the right side is the electrical power loss density. The thermal power loss density is derived from the calculated potential distribution.

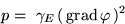$\begin{displaymath}p=~\gamma_E\,(\,\mathop{\mathrm{grad}}\/\varphi\,)^2 \end{displaymath}$

((7)*main::open_tags)

(5) and (6) are coupled by the temperature dependence of the electrical resistivity which is approximated by

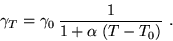$\begin{displaymath}\gamma_T= {\gamma_0\,\frac{1}{1+\alpha\;(T-T_0)}}~. \end{displaymath}$

((8)*main::open_tags)

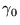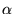Here $\gamma_0$ is the electrical conductivity at the temperature T₀ of 300K, and $\alpha$ is a constant temperature coefficient. This introduces a non-linear behavior and makes it necessary to repeat both the electrical and thermal parts of the simulations several times until an equilibrium establishes.

To overcome the problems with a large sparsely occupied stiffness matrix, a compressed format is used (MSCR) where only nonzero entries are stored. A preconditioned conjugate gradient solver (CG) is used to solve the large linear systems to get the potential and temperature distributions.

Next: APPLICATIONS AND RESULTS Up: No Title Previous: INTERFACING AND GEOMETRIC PROCESSING

Rainer Sabelka
1998-01-30