Die Lösung der Laplace-Gleichung bzw. der Leiterladungsverteilungen stellt ein reines Randwertproblem dar und kann daher mit Randintegralmethoden gelöst werden. Die Reduzierung von einer Volumsdiskretisierung zu einer Oberflächendiskretisierung ist der Hauptvorteil gegenüber finiten Differenz- und Variationsmethoden. Außerdem können Feldprobleme mit unendlich ausgedehntem Gebiet (homogenes Material vorausgesetzt) relativ einfach berechnet werden. Eine effiziente Implementierung der Randintegralmethode für Kapazitätsberechnungen wird in [Nab91] und [Sen92] detailliert dargestellt. Ein Simulator für Widerstandsberechnungen, der mit Randintegralmethoden arbeitet, wird in [Wan92] angegeben.
Das mathematische Gerüst baut auf der Systemantwort einer Punktquelle auf (vergleichbar mit einem Dirac Impuls im Zeitbereich). Die Lösung der Poisson-Gleichung
wobei im gesamten Raum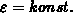 
gelten soll,
ist für eine Punktladung 
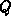, die durch 
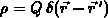, mit der Größe von
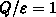an der Stelle 
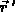(dem Quellpunkt) beschrieben wird,
einfach die Greensche Funktion des unendlichen Raums
Durch die Linearität der Poisson-Gleichung gilt für einen Potentialwert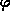 
an der Stelle 
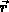bei
gegebener Raumladungsverteilung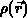 
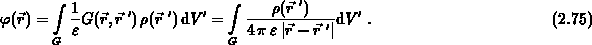
Da aber nur Flächenladungsdichten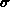 
zu berücksichtigen sind, wird das Volumsintegral auf ein
Flächenintegral reduziert (siehe auch Abbildung 2.2).
Die einfachste Methode, um aus einer bekannten Flächenladungsverteilung 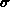auf den 
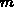Leitern den
Potentialwert 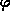an der Stelle 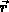numerisch zu berechnen, ist die Point-Matching oder Collocations-Methode.
Dazu diskretisiert man die Leiteroberflächen in finite Flächenstücke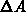 
, ersetzt die variable Ladung
jedes Elementes durch eine konstante gemittelte Ladung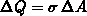 
, die im Flächenschwerpunkt konzentriert
angesetzt wird.
Summiert man über alle Punktquellen, so berechnet man den Potentialwert im Punk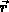t mit
Aus den n Punkten auf dem m Leitern können n Gleichungen zur Berechnung der Potentialverteilung
gebildet werden.
Da die Leiterpotentiale bekannt und die Leiterladungen unbekannt sind, muß zur Lösung der
Integralgleichung (2.76) ein lineares, voll besetztes Gleichungssystem gelöst werden, wobei die Summe
über die Ladungen eines Leiters die gesuchte Leiterladung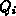 
ergibt.
Will man verschiedene Materialien mit unterschiedlichen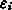 
in die Rechnung einschließen, so
sind auch die Materialgrenzen zu diskretisieren [Ruc87][Elk92].
An den Materialgrenzen wird zusätzlich die Gültigkeit der Sprungbedingung
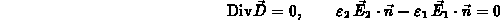
gefordert, wobei nun eine Auswertung der elektrischen Feldstärke notwendig ist.
Allgemein kann die Richtlinie aufgestellt werden, daß Integralmethoden nur dann ihre Geschwindigkeitsvorteile voll ausspielen können, wenn keine oder nur wenige zusätzliche Materialgrenzen zu berücksichtigen bzw. keine homogenen Neumann-Randbedingungen gefordert sind.
