Die Reduktion einer Matrix 
auf eine obere Dreiecksmatrix [U+D]
kann durch eine Gauß-Transformation mit
beschrieben werden. Die Transformationsmatrizen haben die Form
mit
Umgekehrt gilt
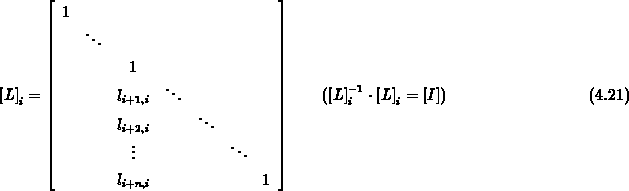
Die Transformationen
sollen zur unteren Dreiecksmatrix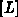 
zusammengefaßt werden, wobei nun
gilt.
Bei einer Implementierung wird die Multiplikation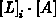 
natürlich auf das betreffende reduzierte 
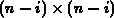große System angewendet
und die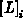 
als eindimensionale Felder abgespeichert. Da das reduzierte System
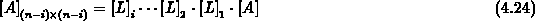
wieder symmetrisch ist
( 
),
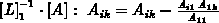genügt es auch, die untere Hälfte der Koeffizientenmatrix abzuspeichern.
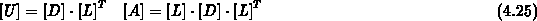
So kann
der Speicheraufwand auf nahezu die Hälfte reduziert werden. Stellen mit alten
Koeffizienten können von neuen Koeffizienten überschrieben werden, wenn man
folgendes berücksichtigt:
Da bei dieser Art der Faktorisierung die Zahlenwerte einer
Spalte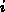 
(siehe (4.18)) erst an die gleiche
Spalte 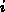in abgespeichert werden können, wenn der Eliminationsschritt
(Multiplikation der Matrix mit 
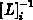) abgeschlossen wurde, ist ein
temporärer Speicherplatz der Länge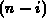 
für die Spalte 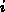anzulegen.
