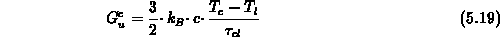5 Eine Energietransportmodellhierarchie




Next: 6 Numerische Methoden
Up: Dissertation Hermann Brand
Previous: 4.6.4 Kontinuumsmechanische Hydrodynamik
Die transporttheoretischen Ergebnisse der letzten drei Kapitel lassen sich
in Form einer Energietransportmodellhierarchie zusammenfassen.
Zur Darstellung der Modellhierarchie wird eine mathematische Formulierung
gewählt, die unabhängig von der Wahl der
Ladungsträgerstatistik
und spezifischer Festlegungen physikalischer Parameter ist.
Auf diese Weise ergibt sich ein formaler Rahmen für ein einheitliches
Energietransportmodell mit gekoppelten
Phononen- und Ladungsträgertemperaturen.
Durch zusätzliche Annahmen und Festlegungen lassen sich verschiedene
Gleichungssysteme
herleiten.
Im komplexesten Fall wird der gekoppelte Transport von Ladungsträgern
und Energie im Halbleiter durch ein System von sechs gekoppelten,
nichtlinearen, partiellen Differentialgleichungen für das elektrostatische
Potential 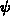 , die Elektronenkonzentration
, die Elektronenkonzentration  , die
Löcherkonzentration
, die
Löcherkonzentration 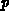 sowie für die Elektronentemperatur
sowie für die Elektronentemperatur 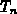 , die Löchertemperatur
, die Löchertemperatur 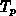 und
die Gittertemperatur
und
die Gittertemperatur 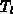 beschrieben.
Das System der Bestimmungsgleichungen genügt den Prinzipien der
irreversiblen Thermodynamik.
Es stellt ein thermoelektrisches Transportmodell der
den Halbleiter konstituierenden Teilsysteme dar.
beschrieben.
Das System der Bestimmungsgleichungen genügt den Prinzipien der
irreversiblen Thermodynamik.
Es stellt ein thermoelektrisches Transportmodell der
den Halbleiter konstituierenden Teilsysteme dar.
Die Thermoelektrizität der Teilsysteme beruht auf
Gesamtenergiebilanzgleichungen des Elektronen-, des Löcher und
des Phononensystems.
Die Systematik der Wechselwirkung der Teilsysteme ergibt sich mit Hilfe
der Gibbs Fundamentalform nach
Prinzipien der irreversiblen Thermodynamik.
Im Unterschied dazu stellt die hydrodynamische Energiebilanzgleichung, die das
zweite Moment der Boltzmanngleichung für einen bestimmten
Ladungsträgertyp darstellt, eine Bilanzgleichung
lediglich der kinetischen Energie des betrachteten Ensembletyps dar.
Die Methode der Momentenentwicklung der Boltzmanngleichung stellt kein
Verfahren zur Verfügung, um die Kopplung hydrodynamischer
Energiebilanzgleichungen herzuleiten.
Wie im vorigen Kapitel gezeigt worden ist, kann prinzipiell auch zu diesem
Zweck die Gibbs Fundamentalform benutzt werden.
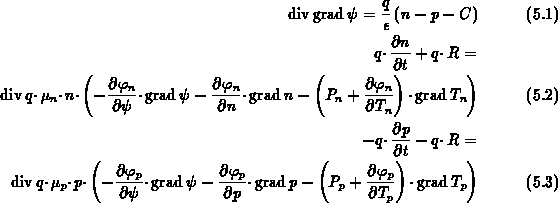
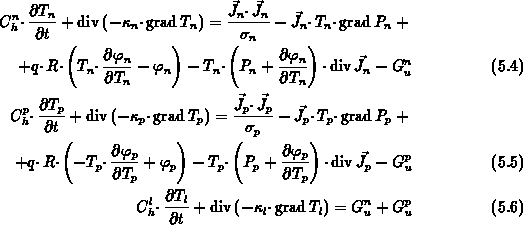
Das Gleichungssystem (5.1), (5.2), (5.3),
(5.4), (5.5), (5.6)
erlaubt die gleichzeitige, selbstkonsistente Bestimmung der
Gitter- und Ladungsträgertemperaturen
zusätzlich zum elektrostatischen Potential
und den Ladungsträgerkonzentrationen.
Es besteht aus der Poissongleichung (5.1),
den Ladungsträgerkontinuitätsgleichungen
(5.2), (5.3),
Gesamtenergiebilanzgleichungen für Elektronen
(5.4)
und Löcher (5.5) sowie einer
Wärmeflußgleichung für das Kristallgittersystem (5.6).
Dieses einheitliche Modell des gekoppelten Phononen- und
Ladungsträgerenergietransports ermöglicht eine konsistente
Beschreibung des Energieaustauschs von Gitter- und Trägersystemen.
Wechselwirkungen und Kopplungen von
Nichtgleichgewichtseffekten der
Trägersysteme aufgrund von
Ladungsträgererwärmung mit
Selbsterwärmungseffekten
des Kristallgitters können erfaßt werden.
Wenn eine einheitliche, homogene Gittertemperatur 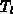 vorausgesetzt wird, kann Gl. (5.6) vernachlässigt werden.
Diese Annahme impliziert, daß sich das Phononensystem wie eine
ideale Wärmesenke mit unendlicher Wärmekapazität und
Wärmeleitfähigkeit verhält.
Das reduzierte Gleichungssystem stellt ein hydrodynamisches Transportmodell
dar.
Im Gegensatz zu [38], [156] enthalten die Bilanzgleichungen der
Ladungsträgerenergie
gemäß den Grundsätzen einer Thermoelektrizität der Teilsysteme
auch die potentielle Energie der Elektronen bzw. Löcher.
Wird umgekehrt angenommen, daß Elektronen, Löcher und Phononen
miteinander im thermischen Gleichgewicht sind, existiert eine einheitliche
Temperatur
vorausgesetzt wird, kann Gl. (5.6) vernachlässigt werden.
Diese Annahme impliziert, daß sich das Phononensystem wie eine
ideale Wärmesenke mit unendlicher Wärmekapazität und
Wärmeleitfähigkeit verhält.
Das reduzierte Gleichungssystem stellt ein hydrodynamisches Transportmodell
dar.
Im Gegensatz zu [38], [156] enthalten die Bilanzgleichungen der
Ladungsträgerenergie
gemäß den Grundsätzen einer Thermoelektrizität der Teilsysteme
auch die potentielle Energie der Elektronen bzw. Löcher.
Wird umgekehrt angenommen, daß Elektronen, Löcher und Phononen
miteinander im thermischen Gleichgewicht sind, existiert eine einheitliche
Temperatur 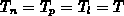 , die jedoch im allgemeinen Fall nicht
uniform ist.
Dieser Grenzfall liefert das thermoelektrische Transportmodell, das zur
Beschreibung von Selbsterwärmungseffekten geeignet ist.
Eine einheitliche Temperatur der Ladungsträger und Phononen erlaubt
die Energiebilanzgleichungen
(5.4), (5.5) und (5.6)
zusammenzufassen.
Es ergibt sich folgendes, reduziertes Gleichungssystem:
, die jedoch im allgemeinen Fall nicht
uniform ist.
Dieser Grenzfall liefert das thermoelektrische Transportmodell, das zur
Beschreibung von Selbsterwärmungseffekten geeignet ist.
Eine einheitliche Temperatur der Ladungsträger und Phononen erlaubt
die Energiebilanzgleichungen
(5.4), (5.5) und (5.6)
zusammenzufassen.
Es ergibt sich folgendes, reduziertes Gleichungssystem:
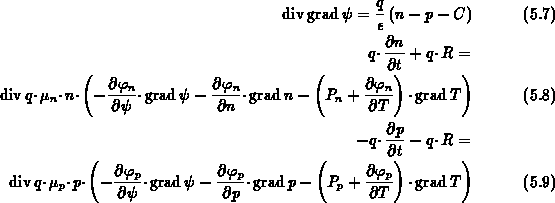
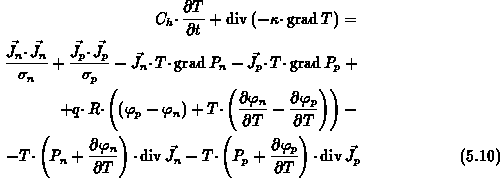
Nimmt man außerdem an, daß die für Ladungsträger und
Kristallgitter einheitliche Temperatur 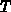 im gesamten Halbleiter
konstant ist, erhält man das Drift-Diffusionsmodell für
isothermischen Ladungsträgertransport:
im gesamten Halbleiter
konstant ist, erhält man das Drift-Diffusionsmodell für
isothermischen Ladungsträgertransport:
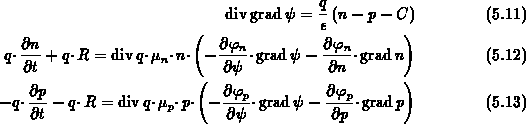
Die Auswertung der Gl. (5.2), (5.3),
(5.4), (5.5) und (5.6) erfordert die
Kenntnis der Abhängigkeit der
Quasifermipotentiale 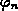 ,
, 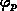 von den jeweiligen
Trägertemperaturen
von den jeweiligen
Trägertemperaturen 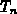 ,
, 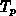 .
Die Ladungsträgerstatistik
ist nicht nur eine Funktion des bandspezifischen Quasifermipotentials
sondern auch der teilchensystemspezifischen Temperatur.
Gl. (2.57), (2.58) bzw. (2.68), (2.69)
können benutzt werden, wenn die jeweilige Trägertemperatur
eingesetzt wird:
.
Die Ladungsträgerstatistik
ist nicht nur eine Funktion des bandspezifischen Quasifermipotentials
sondern auch der teilchensystemspezifischen Temperatur.
Gl. (2.57), (2.58) bzw. (2.68), (2.69)
können benutzt werden, wenn die jeweilige Trägertemperatur
eingesetzt wird:
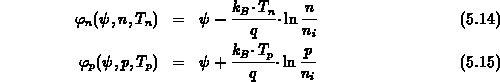
Die Bedingung der Gleichheit der Elektronen- und Löcherkonzentration
im intrinsischen Halbleiter bleibt gültig.
Diese Forderung ergibt:
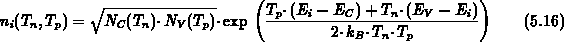
Gl. (5.16) stellt eine Kopplungsbedingung der Trägertemperaturen dar.
Zur Modellierung der Wärmeleitfähigkeit der Elektronen 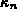 und Löcher
und Löcher 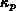 kann das Wiedemann-Franz'sche Gesetz
verwendet werden. Gl. (2.99) und Gl. (3.28) bzw.
(3.29) ergeben:
kann das Wiedemann-Franz'sche Gesetz
verwendet werden. Gl. (2.99) und Gl. (3.28) bzw.
(3.29) ergeben:
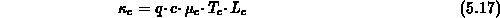
Nach Gl. (5.17) kann die Wärmeleitfähigkeit der
Ladungsträger auf die elektrische
Leitfähigkeit zurückgeführt werden.
Die Lorenzzahl 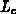 ist im nichtentarteten Halbleiter
gemäß Gl. (3.155) eine Funktion des vom dominierenden
Streumechanismus abhängigen numerischen Parameter
ist im nichtentarteten Halbleiter
gemäß Gl. (3.155) eine Funktion des vom dominierenden
Streumechanismus abhängigen numerischen Parameter 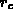 .
Werte für
.
Werte für 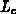 im entarteten Halbleiter sind z.B. in [153] zu finden.
im entarteten Halbleiter sind z.B. in [153] zu finden.
Das einfachste Modell der Wärmekapazitäten der Ladungsträger folgt
aus der Annahme, daß das Elektronen- bzw. Löcherensemble
ein ideales Gas darstellt.
Nach Gl. (4.65) gilt:

Der Energietransfer zwischen den Teilsystemen infolge von Streuprozessen
wird in Gl. (5.4), (5.5), (5.6) durch
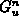 und
und 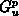 dargestellt.
Wie in Gl. (2.124) können Energierelaxationszeiten definiert werden:
dargestellt.
Wie in Gl. (2.124) können Energierelaxationszeiten definiert werden:
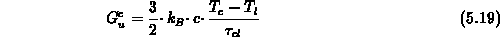
In Gl. (5.19) steckt wie in Gl. (5.18) die Voraussetzung
der Vernachlässigbarkeit der Driftenergie gegenüber der thermischen
Energie des Ladungsträgergases (siehe Gl. (2.116)).




Next: 6 Numerische Methoden
Up: Dissertation Hermann Brand
Previous: 4.6.4 Kontinuumsmechanische Hydrodynamik
Martin Stiftinger
Sat Jun 10 15:00:12 MET DST 1995
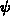 , die Elektronenkonzentration
, die Elektronenkonzentration  , die
Löcherkonzentration
, die
Löcherkonzentration 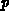 sowie für die Elektronentemperatur
sowie für die Elektronentemperatur 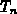 , die Löchertemperatur
, die Löchertemperatur 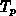 und
die Gittertemperatur
und
die Gittertemperatur 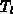 beschrieben.
Das System der Bestimmungsgleichungen genügt den Prinzipien der
irreversiblen Thermodynamik.
Es stellt ein thermoelektrisches Transportmodell der
den Halbleiter konstituierenden Teilsysteme dar.
beschrieben.
Das System der Bestimmungsgleichungen genügt den Prinzipien der
irreversiblen Thermodynamik.
Es stellt ein thermoelektrisches Transportmodell der
den Halbleiter konstituierenden Teilsysteme dar.




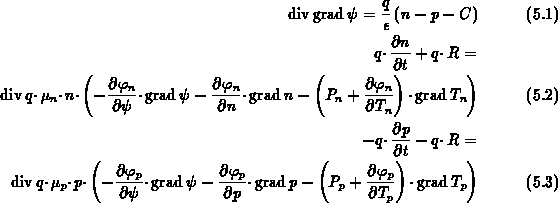
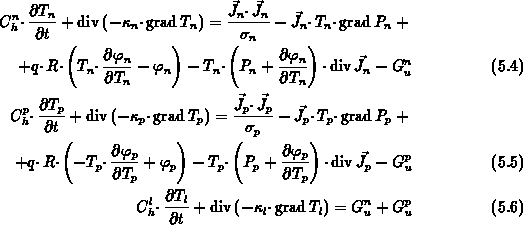
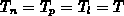 , die jedoch im allgemeinen Fall nicht
uniform ist.
Dieser Grenzfall liefert das thermoelektrische Transportmodell, das zur
Beschreibung von Selbsterwärmungseffekten geeignet ist.
Eine einheitliche Temperatur der Ladungsträger und Phononen erlaubt
die Energiebilanzgleichungen
(
, die jedoch im allgemeinen Fall nicht
uniform ist.
Dieser Grenzfall liefert das thermoelektrische Transportmodell, das zur
Beschreibung von Selbsterwärmungseffekten geeignet ist.
Eine einheitliche Temperatur der Ladungsträger und Phononen erlaubt
die Energiebilanzgleichungen
(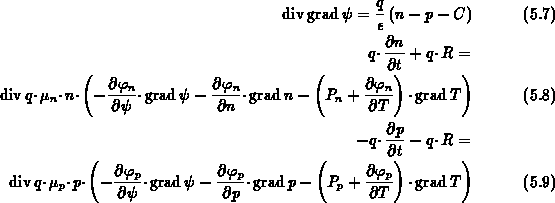
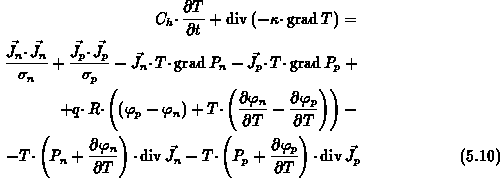
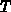 im gesamten Halbleiter
konstant ist, erhält man das Drift-Diffusionsmodell für
isothermischen Ladungsträgertransport:
im gesamten Halbleiter
konstant ist, erhält man das Drift-Diffusionsmodell für
isothermischen Ladungsträgertransport:
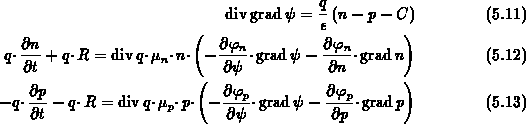
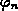 ,
, 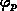 von den jeweiligen
Trägertemperaturen
von den jeweiligen
Trägertemperaturen 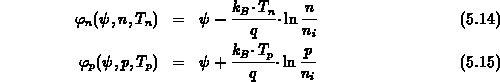
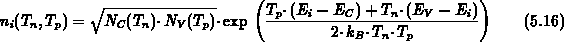
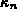 und Löcher
und Löcher 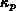 kann das Wiedemann-Franz'sche Gesetz
verwendet werden. Gl. (
kann das Wiedemann-Franz'sche Gesetz
verwendet werden. Gl. (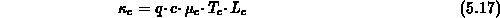
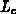 ist im nichtentarteten Halbleiter
gemäß Gl. (
ist im nichtentarteten Halbleiter
gemäß Gl. (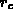 .
Werte für
.
Werte für 
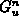 und
und 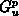 dargestellt.
Wie in Gl. (
dargestellt.
Wie in Gl. (