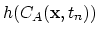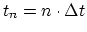Next: 2 Discretization of the
Up: 8 Numerical Handling of
Previous: 8 Numerical Handling of
1 Discretization of the Simple Diffusion Model
The discretization of the simple diffusion models follows directly from the discussion presented in Section 2.3. In order to construct the global matrix of the system, we write nucleus matrix of the simple diffusion model for each
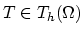 ,
,
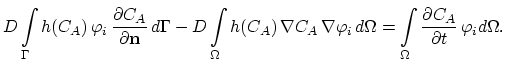 ,
,
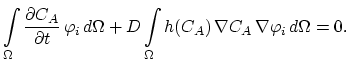 |
(139) |
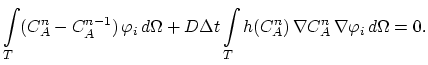 is the time step of the discretisized time and
is the time step of the discretisized time and
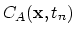 and
and
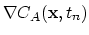 the stiffness and mass matrices defined on single tetrahedra
the stiffness and mass matrices defined on single tetrahedra 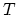 from
from
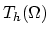 ,
,
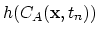 |
|
|
|
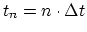 |
|
|
(140) |
for
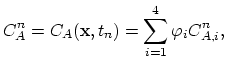 . This problem is linear and the calculation of the nucleus matrix
. This problem is linear and the calculation of the nucleus matrix
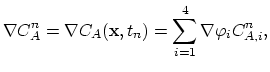 as the Jacobi matrix of the operator
as the Jacobi matrix of the operator
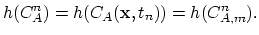 (introduced previously in Section 2.5) is trivial.
(introduced previously in Section 2.5) is trivial.
the global matrix
 is assembled out of the
is assembled out of the
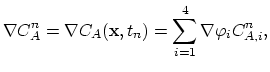 matrices and has obviosly a dimension equal to the number of all points of discretization.
matrices and has obviosly a dimension equal to the number of all points of discretization.




Next: 2 Discretization of the
Up: 8 Numerical Handling of
Previous: 8 Numerical Handling of
J. Cervenka: Three-Dimensional Mesh Generation for Device and Process Simulation
![]() ,
,
![]() ,
,