


Next: 5 Finite Element Scheme
Up: 5 Void evolution and
Previous: 3 Numerical Implementation
4 Setting of the Initial Order Parameter
Profile and Initial Grid Refinement
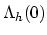
The initial order parameter profile depends on the initial shape of the
void 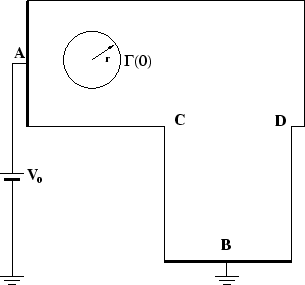 and can be expressed as
and can be expressed as
 |
(263) |
Where
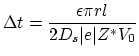 is the signed normal distance of the
point from the initial interface
is the signed normal distance of the
point from the initial interface  . To obtain
sufficient resolution of this initial profile, the basic grid
. To obtain
sufficient resolution of this initial profile, the basic grid 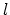 is transformed into grid
is transformed into grid
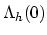 obeying the following
initial grid refinement criterion (IGRC) for the circular
void with center
obeying the following
initial grid refinement criterion (IGRC) for the circular
void with center 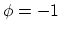 and radius
and radius 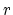 :
:
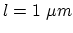 |
(264) |
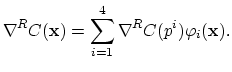 is the chosen number of grid elements across the void-metal
interface width,
is the chosen number of grid elements across the void-metal
interface width, 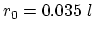 is the longest vertex of the triangle
is the longest vertex of the triangle 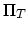 , and
, and
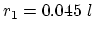 is its center of gravity.
Now an adaptive algorithm defined in Section 4.5.7
transforms the basic grid
is its center of gravity.
Now an adaptive algorithm defined in Section 4.5.7
transforms the basic grid 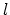 into an initial grid
into an initial grid
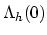 according to
according to 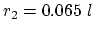 .
.



Next: 5 Finite Element Scheme
Up: 5 Void evolution and
Previous: 3 Numerical Implementation
J. Cervenka: Three-Dimensional Mesh Generation for Device and Process Simulation