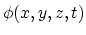Next: 6 Maintaining the Grid
Up: 5 Void evolution and
Previous: 4 Setting of the
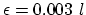 is a triangulation of the area
is a triangulation of the area 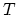 at discrete time
at discrete time 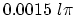 , and
, and
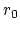 are discrete nodal values of the order parameter on this triangulation.
A finite element based iteration for solving (4.50)
on grid
are discrete nodal values of the order parameter on this triangulation.
A finite element based iteration for solving (4.50)
on grid
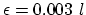 and evaluating the order parameter at the
time
and evaluating the order parameter at the
time
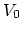 consists of two steps [88]:
consists of two steps [88]:
Step 1. For the 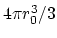 iteration of the
iteration of the 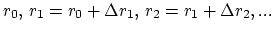 time step
the linear system of equations has to be solved:
time step
the linear system of equations has to be solved:
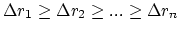 |
(265) |
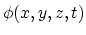 |
(266) |
where
 |
(267) |
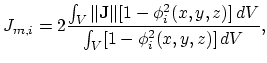 |
(268) |
for each 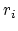 of the nodal values
of the nodal values
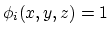 of the
triangulation
of the
triangulation
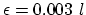 .
. ![$ [M]_{ij}$](img908.png) and
and ![$ [K]_{ij}$](img909.png) are the lumped mass
and stiffness matrix, respectively and
are the lumped mass
and stiffness matrix, respectively and
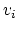 .
.
Step 2.
All nodal values
 are projected on
are projected on ![$ [-1, 1]$](img912.png) by a function
by a function
 |
(269) |
For solving (4.52) a conventional finite element scheme is
applied [76].




Next: 6 Maintaining the Grid
Up: 5 Void evolution and
Previous: 4 Setting of the
J. Cervenka: Three-Dimensional Mesh Generation for Device and Process Simulation
![]() is a triangulation of the area
is a triangulation of the area ![]() at discrete time
at discrete time ![]() , and
, and
![]() are discrete nodal values of the order parameter on this triangulation.
A finite element based iteration for solving (4.50)
on grid
are discrete nodal values of the order parameter on this triangulation.
A finite element based iteration for solving (4.50)
on grid
![]() and evaluating the order parameter at the
time
and evaluating the order parameter at the
time
![]() consists of two steps [88]:
consists of two steps [88]:
![]() iteration of the
iteration of the ![]() time step
the linear system of equations has to be solved:
time step
the linear system of equations has to be solved: