


Next: 4.3 Bulk Mobility of
Up: 4. Mobility Modeling
Previous: 4.1 Semiconductor Device Equations
Subsections
4.2 Modeling Approaches
The mobility behavior in a MOS transistor can be classified into: (i) low field
bulk mobility (ii) surface/inversion layer mobility and (iii) high field
mobility. In the low electric field regime, the charge carriers are almost in
equilibrium with the lattice and the mobility has a characteristic low-field
value that is commonly denoted by the symbol 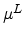 . The value of this
mobility is dependent upon phonon and impurity scattering.
. The value of this
mobility is dependent upon phonon and impurity scattering.
Modeling of carriers in the inversion layer poses additional complications. In
the inversion layer, the carriers are subject to surface scattering,
carrier-carrier scattering and quantum mechanical confinement. All these
effects cause mobility degradation. The transverse electric field originating
from the applied gate bias often serves as a parameter to indicate the strength
of the inversion layer phenomena.
The high field behavior shows that the carrier mobility declines with electric
field because the carriers that gain energy experience larger scattering
rates. The mean drift velocity no longer increases linearly with increasing
electric field, but rises more slowly. Eventually, the velocity saturates at a
constant value. This saturation velocity is commonly denoted by the symbol
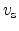 . Impurity scattering is relatively insignificant for energetic
carriers, and so
. Impurity scattering is relatively insignificant for energetic
carriers, and so 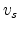 is primarily a function of the lattice temperature.
is primarily a function of the lattice temperature.
The modeling approaches of physical parameters such as the mobility can be
subdivided into three categories: [Mujtaba95]
- Physically based: Mathematical expressions describing the physical
effects are derived using first principle calculations. To capture the entire
physical model into a closed form solution in which the parameter dependencies
are obtained from fundamental calculations, considerable simplifying
assumptions have to be made.
- Semi-empirical: This approach arises because in practice it is seldom the
case that the physically-based models conform to the experimental
data. Therefore, to reconcile the model with experimental data, the
coefficients appearing in the physically-based model are allowed to vary from
their original values while certain dependencies resulting from the first
principles calculation are retained.
- Empirical: Empirically-based models are those in which all dependencies
are allowed to vary. Compared to the other two approaches, this modeling
approach generally tends to obscure the important physics thereby exhibiting a
narrower range of validity. Empirical models are usually resorted to when the
dependencies predicted by the first principles calculation do not allow a good
fit between the experimental data and the corresponding semi-empirical
model. These models are usually more efficient in comparison to the other two
modeling approaches.
The Monte Carlo (MC) method is a widely used statistical numerical technique
for simulating the behavior of various complex physical and mathematical
systems. The method was first applied by Kurosawa [Kurosawa66] for
solving the Boltzmann transport equation which governs the motion of electrons
and holes in semiconductors. Within this technique a particle trajectory is
constructed as a sequence of free flights and scattering events. The free
flight times between collisions and the parameters of the scattering events are
generated stochastically using probabilities of the microscopic processes. Thus
the main advantage of this approach is the direct description of the
microscopic particle dynamics. The numerical band structures of different
semiconductors can be taken into account. The method was subsequently improved
and applied to comprehensively study the electron transport in Si and
Ge [Jacoboni83].
A distinct advantage of the Monte Carlo method is its ability to provide a
solution of the BTE without compromising on the basic physical models for band
structure and scattering processes. However, due to the statistical nature of
the method, large simulation times are needed for performing full device
simulations, in order to obtain meaningful average quantities of interest and
to reduce the stochastic error.
In this work, the effect of strain on the electronic transport properties has
been investigated using the Vienna Monte Carlo Simulator (VMC). It offers
simulation algorithms for both bulk semiconductors and one-dimensional devices
based on analytical band and full-band models. Additionally, a fast zero-field
algorithm is included [Smirnov03]. VMC provides a mature set of
scattering models including phonon scattering, ionized impurity scattering,
alloy scattering, and impact ionization. Details concerning the scattering
models implemented can be found in the documentation [IuE06].



Next: 4.3 Bulk Mobility of
Up: 4. Mobility Modeling
Previous: 4.1 Semiconductor Device Equations
S. Dhar: Analytical Mobility Modeling for Strained Silicon-Based Devices
![]() . Impurity scattering is relatively insignificant for energetic
carriers, and so
. Impurity scattering is relatively insignificant for energetic
carriers, and so ![]() is primarily a function of the lattice temperature.
is primarily a function of the lattice temperature.