[next] [prev] [prev-tail] [tail] [up]

3.5 Monte Carlo integration

The terms comprising a Neumann series contain high-dimensional integrals which can be efficiently calculated using stochastic sampling by Monte Carlo techniques.

Consider an integral

∫ b ∫ I ≡ dxϕ (x) = dxp (x )ψ(x) , (3.23) a
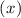where p is a probability density function such that ∫ abdxp(x) = 1 and ψ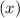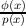(x) = ϕ(x) p(x). The integral I corresponds to the mean value of ψ (x).

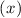The choice of the distribution p determines various qualities of the Monte Carlo algorithm [106], namely the computational efficiency, the convergence rate and the associated trade-off with reliability (variance in the result). Often physical considerations are used to choose the distribution p.

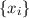Consider the random variables X and Ψ[X ]: A sequence of N numbers {xi} is generated according to p and is used to sample Ψ [X ], thereby approximating the mean value by an expected value:

N I ≈ E [Ψ [X ]] =-1 ∑ ψ (x) . (3.24) N i=1 i

This establishes the link between the Neumann series and the Monte Carlo algorithm, which will be discussed in Section 3.7.

[next] [prev] [prev-tail] [front] [up]