


Next: 7. Case Studies
Up: 6. Negative Bias Temperature
Previous: 6.5 Tsetseris' Model
Subsections
6.6 The New Model for Numerical Simulation of NBTI
Figure 6.16:
Schematic illustration of the model as implemented in Minimos-NT
giving an overview of the involved processes.
|
|
From literature it is obvious that no clear consensus about the physical
mechanism nor a model which is commonly agreed upon is found up to now.
Various research groups report different key mechanisms leading to NBTI
and therefore propose different models which sometimes completely contradict
each other [85,110,102,86,122]. Is it purely
the interface degradation, are oxide traps or oxide charges involved, is hole
trapping important, are Si-H or also Si-O bonds broken et cetera.
In this section a model is proposed which was implemented into the numerical
device simulator Minimos-NT. Figure 6.16 gives an
overview of the involved processes. The model is able to achieve excellent
agreement with measurement data on thick, pure
 dielectrics of
high-voltage devices from our industry partner (Section 7.1) for both,
the stress and the relaxation phase of NBTI and for different temperatures.
dielectrics of
high-voltage devices from our industry partner (Section 7.1) for both,
the stress and the relaxation phase of NBTI and for different temperatures.
As the model comprises of many models and physical assumptions described in
different parts of this work, I will collect all important equations in this
section for the sake of clarity.
The first mechanism is the interface degradation as proposed in the
reaction-diffusion model (Section 6.4). It is described in form of a
balance equation between generation of electrically active interface traps
(
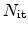 ) due to a forward term, and interface trap annealing as a result of a
backward term as follows
) due to a forward term, and interface trap annealing as a result of a
backward term as follows
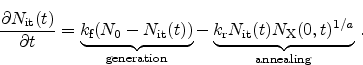 |
(6.31) |
The important parameters in this equation are the forward reaction rate,
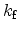 ,
the sum of passivated and broken interface states
,
the sum of passivated and broken interface states
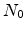 , the reverse reaction
rate
, the reverse reaction
rate
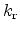 , the amount of the mobile species
, the amount of the mobile species
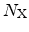 directly available at the
interface, and the kinetics exponent,
directly available at the
interface, and the kinetics exponent, 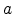 , giving the type of mobile species.
, giving the type of mobile species.
Assuming electrically neutral hydrogen,
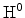 , or hydrogen protons,
, or hydrogen protons,
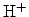 ,
the kinetics exponent
,
the kinetics exponent 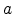 equals
equals 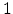 . In this case, for every generated
. In this case, for every generated
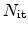 a mobile hydrogen,
a mobile hydrogen,
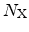 , is released. To assume molecular hydrogen,
, is released. To assume molecular hydrogen,
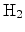 ,
as the mobile species the kinetics exponent equals
,
as the mobile species the kinetics exponent equals 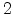 .
.
The amount of interface states
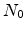 is strongly dependent on the wafer
orientation and the process technology. It can greatly differ for different
is strongly dependent on the wafer
orientation and the process technology. It can greatly differ for different
 interfaces. Reasonable values are often in the range of
interfaces. Reasonable values are often in the range of
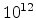 -
-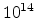 cm
cm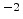 as described in Section 3.1.
For reliable device operation it is, of course, of highest interest to keep
this number as low as possible.
as described in Section 3.1.
For reliable device operation it is, of course, of highest interest to keep
this number as low as possible.
The forward reaction rate is dependent on the local electric field,
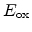 , and
the local hole concentration
, and
the local hole concentration
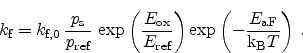 |
(6.32) |
Here,
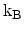 is the Boltzmann constant and
is the Boltzmann constant and 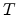 the temperature. The prefactor
the temperature. The prefactor
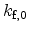 , the reference hole concentration
, the reference hole concentration
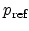 , and the reference electric
field
, and the reference electric
field
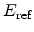 are model calibration parameters. The temperature dependence is
introduced by an Arrhenius' law of the activation energy
are model calibration parameters. The temperature dependence is
introduced by an Arrhenius' law of the activation energy
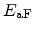 , which is also
a calibration parameter. The influence of the electric field in this equation
is exponential and change in the field has therefore a major impact on the
forward reaction rate while the hole concentration has only little impact in
agreement with experimental observations [101].
, which is also
a calibration parameter. The influence of the electric field in this equation
is exponential and change in the field has therefore a major impact on the
forward reaction rate while the hole concentration has only little impact in
agreement with experimental observations [101].
The reverse reaction rate is also introduced as Arrhenius activated with the
activation energy
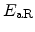 and the prefactor
and the prefactor
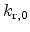
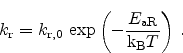 |
(6.33) |
As described in Section 3.1, the energy distribution of
electrically active interface traps
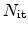 can be very important. When the
Fermi-level is not very close to one of the band edges, the charge state of
these traps differs depending on their density-of-states (DOS). The density of
can be very important. When the
Fermi-level is not very close to one of the band edges, the charge state of
these traps differs depending on their density-of-states (DOS). The density of
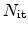 is given as the integral of
is given as the integral of
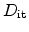 across the whole band-gap
across the whole band-gap
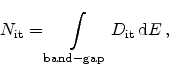 |
(6.34) |
or, when considering the amphoteric nature of the traps with their double peaks
(Section 3.1.1)
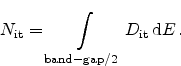 |
(6.35) |
Several models for different DOS are available in Minimos-NT, where the most
plausible according to literature are two peaks of Gaussian form as found in
Section 3.1.2.
The next mechanism in the degradation process is the (drift-) diffusion of the
hydrogen related species
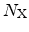 from the
from the
 interface into the dielectric.
interface into the dielectric.
The convection of the electrically neutral species
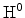 and
and
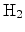 is
a purely diffusive process due to the concentration gradient
is
a purely diffusive process due to the concentration gradient
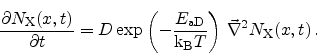 |
(6.36) |
Here, 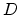 is the diffusion constant. The temperature dependence was introduced
using Arrhenius' law with the activation energy
is the diffusion constant. The temperature dependence was introduced
using Arrhenius' law with the activation energy
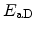 .
.
For the case of proton transport,
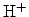 , an additional drift term has to be
added to (6.36). In the typical NBT stress condition
where a negative voltage is applied to the gate contact, this leads to quick
removal of the positively charged protons from the interface. As a consequence
more interface traps can break and the degradation is increased.
, an additional drift term has to be
added to (6.36). In the typical NBT stress condition
where a negative voltage is applied to the gate contact, this leads to quick
removal of the positively charged protons from the interface. As a consequence
more interface traps can break and the degradation is increased.
To account for the dispersive transport theory as described in
Section 6.4.3, the trapping and de-trapping of the mobile
species in the dielectric is included in this model.
At each trap center in the dielectric a balance equation is solved to account
for the trapping and de-trapping effects. The trap occupancy
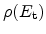 is
considered at each trap energy level
is
considered at each trap energy level
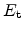 as
as
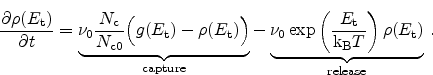 |
(6.37) |
Here,
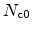 is the hydrogen effective density-of-states,
is the hydrogen effective density-of-states,
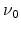 the release
rate coefficient,
the release
rate coefficient,
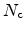 the amount of available, uncaptured hydrogen and
the amount of available, uncaptured hydrogen and
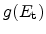 the trap density-of-states at this energy level. In the capture part
of this equation the filling of traps is accounted for (
the trap density-of-states at this energy level. In the capture part
of this equation the filling of traps is accounted for (
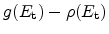 )
so that the maximum possible amount of trapped hydrogen at each trap level
equals the DOS. The release of hydrogen is dependent on the ``depth'' of the
trap. Deeper traps have an exponential decrease in their de-trapping
probability.
)
so that the maximum possible amount of trapped hydrogen at each trap level
equals the DOS. The release of hydrogen is dependent on the ``depth'' of the
trap. Deeper traps have an exponential decrease in their de-trapping
probability.
The trap energy
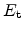 is zero at the mobility edge and below zero at the trap
levels with more negative values for deeper traps. Therefore, with decreasing
temperature the trap release rate decreases (
is zero at the mobility edge and below zero at the trap
levels with more negative values for deeper traps. Therefore, with decreasing
temperature the trap release rate decreases (
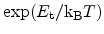 ) and de-trapping
becomes more unlikely. The trapping probability does not change in this model.
) and de-trapping
becomes more unlikely. The trapping probability does not change in this model.
Within the model the charge state of trapped hydrogen can be chosen to model
the formation of positively charged trapped protons, as described
in [107].
The DOS of the trap levels can be selected from the model. Two plausible
densities are schematically illustrated on the right hand side of
Figure 6.16. An exponential distribution with the
highest DOS at the band edge [88] or with an additional Gaussian
peak in deeper states forming deep and therefore ``slow''
traps [106,107,108].
Table 6.1:
NBTI model parameters.
| Parameter |
Unit |
Description |
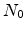 |
cm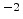 |
Total density of interface states (el. active and
inactive) |
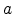 |
1 |
Kinetics exponent automatically set according to
diffusing species |
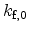 |
s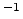 |
Forward reaction rate prefactor |
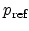 |
cm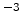 |
Reference hole concentration |
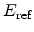 |
V cm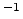 |
Reference electric field |
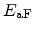 |
eV |
Forward reaction activation energy |
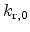 |
cm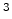 s s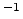 |
Reverse reaction rate prefactor |
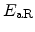 |
eV |
Reverse reaction activation energy |
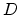 |
cm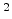 s s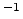 |
Diffusion coefficient |
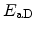 |
eV |
Diffusion activation energy |
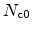 |
cm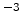 |
Hydrogen effective density-of-states |
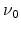 |
s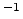 |
Trapping/de-trapping frequency |
|

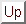


Next: 7. Case Studies
Up: 6. Negative Bias Temperature
Previous: 6.5 Tsetseris' Model
R. Entner: Modeling and Simulation of Negative Bias Temperature Instability
![\includegraphics[width=16cm]{figures/nbti-mmnt-model-schematic}](img592.png)
![\includegraphics[width=16cm]{figures/nbti-mmnt-model-schematic}](img592.png)
![]() dielectrics of
high-voltage devices from our industry partner (Section 7.1) for both,
the stress and the relaxation phase of NBTI and for different temperatures.
dielectrics of
high-voltage devices from our industry partner (Section 7.1) for both,
the stress and the relaxation phase of NBTI and for different temperatures.
![]() , or hydrogen protons,
, or hydrogen protons,
![]() ,
the kinetics exponent
,
the kinetics exponent ![]() equals
equals ![]() . In this case, for every generated
. In this case, for every generated
![]() a mobile hydrogen,
a mobile hydrogen,
![]() , is released. To assume molecular hydrogen,
, is released. To assume molecular hydrogen,
![]() ,
as the mobile species the kinetics exponent equals
,
as the mobile species the kinetics exponent equals ![]() .
.
![]() is strongly dependent on the wafer
orientation and the process technology. It can greatly differ for different
is strongly dependent on the wafer
orientation and the process technology. It can greatly differ for different
![]() interfaces. Reasonable values are often in the range of
interfaces. Reasonable values are often in the range of
![]() -
-![]() cm
cm![]() as described in Section 3.1.
For reliable device operation it is, of course, of highest interest to keep
this number as low as possible.
as described in Section 3.1.
For reliable device operation it is, of course, of highest interest to keep
this number as low as possible.
![]() , and
the local hole concentration
, and
the local hole concentration
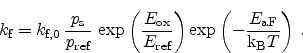
![]() and the prefactor
and the prefactor
![]()
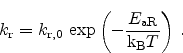
![]() can be very important. When the
Fermi-level is not very close to one of the band edges, the charge state of
these traps differs depending on their density-of-states (DOS). The density of
can be very important. When the
Fermi-level is not very close to one of the band edges, the charge state of
these traps differs depending on their density-of-states (DOS). The density of
![]() is given as the integral of
is given as the integral of
![]() across the whole band-gap
across the whole band-gap
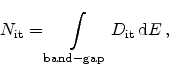
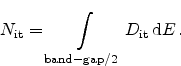
![]() and
and
![]() is
a purely diffusive process due to the concentration gradient
is
a purely diffusive process due to the concentration gradient
![]() , an additional drift term has to be
added to (6.36). In the typical NBT stress condition
where a negative voltage is applied to the gate contact, this leads to quick
removal of the positively charged protons from the interface. As a consequence
more interface traps can break and the degradation is increased.
, an additional drift term has to be
added to (6.36). In the typical NBT stress condition
where a negative voltage is applied to the gate contact, this leads to quick
removal of the positively charged protons from the interface. As a consequence
more interface traps can break and the degradation is increased.
![]() is
considered at each trap energy level
is
considered at each trap energy level
![]() as
as
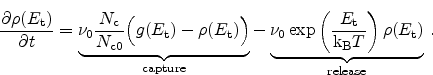
![]() is zero at the mobility edge and below zero at the trap
levels with more negative values for deeper traps. Therefore, with decreasing
temperature the trap release rate decreases (
is zero at the mobility edge and below zero at the trap
levels with more negative values for deeper traps. Therefore, with decreasing
temperature the trap release rate decreases (
![]() ) and de-trapping
becomes more unlikely. The trapping probability does not change in this model.
) and de-trapping
becomes more unlikely. The trapping probability does not change in this model.