A. Line-Triangle Intersection

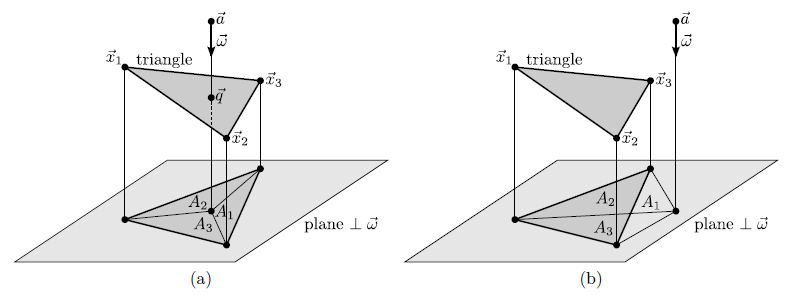
For the initialization of the LS function, triangles must be checked for possible intersections with grid lines (see Section 4.1.1). In the following, a robust line-triangle intersection test is presented. If the line intersects the triangle, the intersection point is also calculated. The following approach ensures that, if a line close to an edge fails the intersection test due to numerical errors, the test will succeed for another triangle, which is adjacent to the same edge. Hence, if a surface is given as a triangulation, cases, where the line fails all intersection tests, although it intersects the surface, are avoided.

A triangle with vertices ${\vec{x}}_1$ , ${\vec{x}}_2$ , and ${\vec{x}}_3$ is intersected by a line defined by point ${\vec{a}}$ and unit vector ${\vec{\omega}}$ , if the (signed) areas

$${A}_i := \frac{1}{2}\left(\left({\vec{x}}_{i+1}-{\vec{a}}\right) ... ...2} \det( {\vec{x}}_{i+1}-{\vec{a}}, {\vec{x}}_{i+2}-{\vec{a}}, {\vec{\omega}} )$$ (A.1)

are either all non-negative or all non-positive. The sign is given by the triangle orientation with respect to ${\vec{\omega}}$ . All the index summations in (A.1) are modulo 3 plus 1. ${A}_i$ corresponds to the area of the triangle spanned by the vectors ${\vec{x}}_{i+1}$ , ${\vec{x}}_{i+2}$ , and $\vec{a}$ , if it is projected onto a plane perpendicular to ${\vec{\omega}}$ (see Figure A.1). If all ${A}_i$ are equal to zero, the grid line is in the same plane as the triangle, or the triangle is degenerated. In both cases the line is considered to not intersect the triangle.

Figure A.1: The line defined by the point $\vec{a}$ and the unit vector ${\vec{\omega}}$ intersects the triangle given by ${\vec{x}}_1$ , ${\vec{x}}_2$ , and ${\vec{x}}_3$ , if the signed areas ${A}_1$ , ${A}_2$ , and ${A}_3$ have the same sign. (a) ${A}_1<0$ , ${A}_2<0$ , and ${A}_3<0$ , which implies that the line intersects the triangle. (b) No intersection, since ${A}_1>0$ , ${A}_2<0$ , and ${A}_3<0$ .

To guarantee that lines close to an edge succeed the intersection test for any of the two adjacent triangles, the numerical evaluation of (A.1) must preserve the anticommutativity with respect to ${\vec{x}}_{i+1}$ and ${\vec{x}}_{i+2}$ . However, due to numerical errors this is usually not the case. For example, the numerical result of $a\cdot b - c\cdot d$ is not necessarily the same as that of $c\cdot d - a\cdot b$ with opposite sign [100]. To overcome this problem, the two vectors ${\vec{x}}_{i+1}$ and ${\vec{x}}_{i+2}$ in (A.1) are compared using an order relation, such as lexicographical comparison. If ${\vec{x}}_{i+1}$ is larger than ${\vec{x}}_{i+2}$ , the two vectors are swapped, and the final result of (A.1) is inverted. This technique ensures the anticommutativity in (A.1).

Once the areas ${A}_i$ are determined and the intersection test is positive, the intersection point ${\vec{q}}$ can be obtained by

$${\vec{q}} = \frac{\sum_{i=1}^3{A}_i\cdot{\vec{x}}_i}{{A}} = \sum_{i=1}^3\frac{{A}_i}{{A}}\cdot{\vec{x}}_i \ {A}:=\sum_{i=1}^3{A}_i.$$ (A.2)

As defined earlier, an intersection only occurs, if all ${A}_i$ are non-negative or non-positive, while not all are equal to zero. Therefore, the denominator ${A}$ in (A.2) never vanishes. To avoid potential overflows the second variant for the calculation of the intersection point is preferable. There, the coefficients $\frac{{A}_i}{{A}}$ are always in the range $\left[0,1\right]$ and the calculation of the intersection point is safe.