| (4.1) |
As mentioned in Section 3.1.3 the LS function is usually initialized as a signed distance function. In case of the sparse field LS method it is better to use the smallest (signed) Manhattan distance
It is not necessary to calculate the initial LS values for the entire grid. Only grid points close to the boundary have to be considered. In particular, the sparse field method requires the determination of all active grid points together with their LS values only at the beginning. If the sign of the LS function is known for all other grid points, the additional layers can be determined using (3.28). The required LS values can then be computed using (3.29). The knowledge of the sign for the LS values at all points of the grid is also a prerequisite for the setup of the H-RLE data structure.
The signs of the LS values are unambiguously defined, if the set of all grid points with an opposite signed neighbor is known. This set of grid points clearly separates the positive and the negative grid points from each other. To satisfy all the requirements for the initialization of the sparse field method and the H-RLE data structure, the LS framework determines all grid points for which the LS value is in the range
![]() .
.
This set of grid points contains all the required information, because due to (4.1) all grid points are included, which have an opposite signed neighbor. Before setting up the H-RLE data structure, the LS framework collects all these grid points together with their LS values and stores them in a list. In the following sections an efficient technique is described to obtain this list in linear time.
Since the Manhattan distance is only needed for grid points close to the boundary, the distance computation can be simplified. For these points the Manhattan distance can be approximated by the smallest distance to the boundary along any paraxial direction. In other words, the smallest unsigned distance of a grid point is approximated by
| (4.2) |
In practice the distance transform is carried out by an iteration over all segments of the discretized boundary representation. For each segment all intersecting grid lines are determined. The number of possible grid lines can be confined using the bounding box of the segment. In the two-dimensional case the test whether a grid line intersects a line segment or not is trivial. In the three-dimensional case the intersection test with a triangle is more difficult and is described in Appendix A. For each intersecting grid line the intersection point
![]() is calculated and all grid points
is calculated and all grid points ![]() on that grid line are considered for which
on that grid line are considered for which
The signed distance of a grid point ![]() to the current segment is given by
to the current segment is given by
|
If for each grid point ![]() the distance with the smallest absolute value
the distance with the smallest absolute value
![]() is kept, at least all grid points with LS values in the range
is kept, at least all grid points with LS values in the range
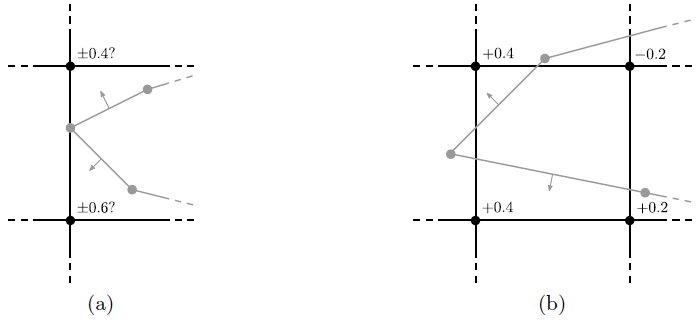
![]() will be properly initialized after iterating over all segments of the boundary mesh. However, this procedure can lead to problems as depicted in Figure 4.2a, where the wrong sign could be assigned to the LS value of both grid points, since both segments are equally distanced. To resolve this ambiguity without additional consideration of neighbor segments, another distance is measured using
will be properly initialized after iterating over all segments of the boundary mesh. However, this procedure can lead to problems as depicted in Figure 4.2a, where the wrong sign could be assigned to the LS value of both grid points, since both segments are equally distanced. To resolve this ambiguity without additional consideration of neighbor segments, another distance is measured using
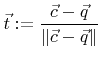 with with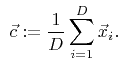 |
(4.6) |
The initialization procedure is now as follows: For each segment and for all intersecting grid lines all grid points fulfilling (4.3) are determined. The indices ![]() of these grid points are appended to a list along with their corresponding distances
of these grid points are appended to a list along with their corresponding distances ![]() and
and ![]() , defined in (4.4) and (4.5), respectively. Finally the list is lexicographically sorted with respect to the grid point indices. If there are more entries with the same
, defined in (4.4) and (4.5), respectively. Finally the list is lexicographically sorted with respect to the grid point indices. If there are more entries with the same ![]() , (which is not very often the case,)
, (which is not very often the case,) ![]() of that entry with the smallest corresponding
of that entry with the smallest corresponding ![]() is used for the initial LS value
is used for the initial LS value
![]() .
.
The entire initialization algorithm has a complexity of
![]() , where
, where
![]() is the final number of defined grid grid points in the H-RLE data structure.
is the final number of defined grid grid points in the H-RLE data structure.
![]() is the total number of segments of the boundary mesh. The logarithmic term is due to the sorting algorithm which cannot be avoided, since the setup of the H-RLE data structure requires a sorted list as well. This initialization algorithm can produce inefficient sets of active grid points as exemplified in Figure 4.2b, which can be avoided by appending a pruning procedure, as mentioned earlier (see Section 3.4.2).
is the total number of segments of the boundary mesh. The logarithmic term is due to the sorting algorithm which cannot be avoided, since the setup of the H-RLE data structure requires a sorted list as well. This initialization algorithm can produce inefficient sets of active grid points as exemplified in Figure 4.2b, which can be avoided by appending a pruning procedure, as mentioned earlier (see Section 3.4.2).