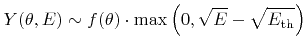Next: 2.3 Surface Kinetics
Up: 2.2 Transport Kinetics
Previous: 2.2.2 Feature-Scale Transport
2.2.3 Reemission
For the determination of the arrival flux distribution  the reemitted flux distribution
the reemitted flux distribution
 must be known. This work assumes that the reemission is related to the incident flux distribution by
must be known. This work assumes that the reemission is related to the incident flux distribution by
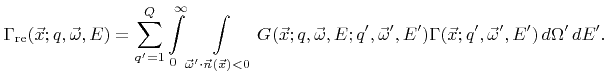 |
(2.15) |
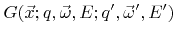 is the reemission probability function which describes the conditional probability for the emission of a particle of species
is the reemission probability function which describes the conditional probability for the emission of a particle of species 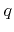 and energy
and energy 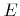 into direction
into direction
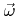 , if a particle of species
, if a particle of species 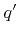 , direction
, direction
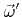 , and energy
, and energy 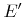 strikes the surface at point
strikes the surface at point
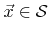 .
. 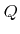 is the number of process relevant particle species. This model assumes that the time between the incidence and the induced reemissions is negligible. A further assumption is that the new particles are reemitted exactly from the same location, where the incident particle has hit the surface.
is the number of process relevant particle species. This model assumes that the time between the incidence and the induced reemissions is negligible. A further assumption is that the new particles are reemitted exactly from the same location, where the incident particle has hit the surface.
The description, using the reemission probability function, is quite general in the sense that many effects can be properly treated. For example, perfect reflection of particles of type 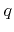 would be described by
would be described by
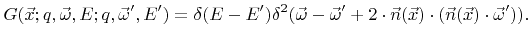 |
(2.16) |
A more realistic description of specular-like reflexions of ions is given in [15]. If the incident direction is given by the azimuthal and the polar angle
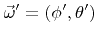 relative to the surface normal
relative to the surface normal 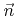 with
with
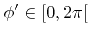 and
and
![$ {\theta}'\in\left]\frac{\pi}{2},\pi\right]$](img223.png) , then the average reemitted direction is
, then the average reemitted direction is
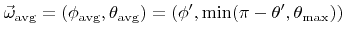 . Here
. Here
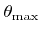 is a constant parameter smaller than, but close to
is a constant parameter smaller than, but close to
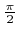 . The reemitted direction
. The reemitted direction
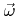 is distributed around
is distributed around
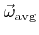 according to
according to
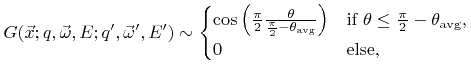 |
(2.17) |
with
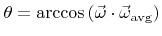 .
.
Diffusive reemission of a neutral particle species
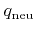 is usually described by the relation
is usually described by the relation
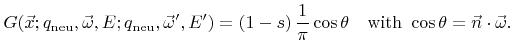 |
(2.18) |
Here 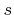 is the probability that an incident particle remains sticking on the surface. The directional distribution of diffusive reemitted particles follows the Knudsen cosine law [37]. Since the total kinetic energy of neutrals is usually given only by their thermal energy, the energy distribution of neutrals can be neglected.
is the probability that an incident particle remains sticking on the surface. The directional distribution of diffusive reemitted particles follows the Knudsen cosine law [37]. Since the total kinetic energy of neutrals is usually given only by their thermal energy, the energy distribution of neutrals can be neglected.
The incidence of high energetic ions can lead to sputtering of particles on the surface, which are redeposited somewhere else. For example, if
 denotes ions and
denotes ions and
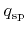 denotes a sputtered particle type for which the kinetic energy can be neglected and a cosine-like directional distribution can be assumed, the reemission probability function takes the form [60]
denotes a sputtered particle type for which the kinetic energy can be neglected and a cosine-like directional distribution can be assumed, the reemission probability function takes the form [60]
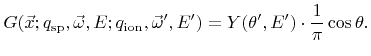 |
(2.19) |
Here
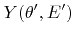 is a yield function describing the average number of sputtered particles per incidence of an ion at angle
is a yield function describing the average number of sputtered particles per incidence of an ion at angle 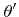 and energy
and energy 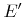 . Commonly, yield functions are approximated by
. Commonly, yield functions are approximated by
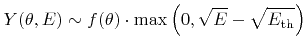 |
(2.20) |
This reflects the observed linear growth with the root of the incident energy 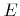 , which must be larger than the threshold energy
, which must be larger than the threshold energy
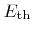 to permit sputtering [120]. The angular dependence is usually obtained by measurements. A semi-empirical formula was proposed by Yamamura et al. [76,136]
to permit sputtering [120]. The angular dependence is usually obtained by measurements. A semi-empirical formula was proposed by Yamamura et al. [76,136]
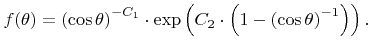 |
(2.21) |
Here 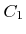 and
and 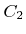 are positive fitting parameters. For
are positive fitting parameters. For
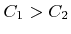 this function exhibits a maximum at inclined incidence and is decreasing towards zero for
this function exhibits a maximum at inclined incidence and is decreasing towards zero for
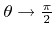 .
.
In general, the reemission probability function may itself depend on the flux distribution
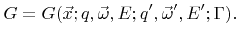 |
(2.22) |
For example, the sticking probability in (2.18) can depend on the so-called surface coverage which describes the fraction of occupied surface sites. The coverage may be influenced by the fluxes of inhibitors which adsorb on the surface and lead to some passivation of the surface. If the reemission probability function shows a dependence on the flux distributions,
(2.15) will be non-linear and the calculation of the particle transport will get more complicated. This issue will be addressed in further detail in Section 5.4.1.
Finally, it should be noted that in the presence of different material regions the reemission probabilities are also dependent on the material type on the surface. As an example, the type and the number of sputtered particles vary with the material on the surface. Therefore, for each material type exposed during the process, an individual reemission probability function must be defined.




Next: 2.3 Surface Kinetics
Up: 2.2 Transport Kinetics
Previous: 2.2.2 Feature-Scale Transport
Otmar Ertl: Numerical Methods for Topography Simulation
![]() the reemitted flux distribution
the reemitted flux distribution
![]() must be known. This work assumes that the reemission is related to the incident flux distribution by
must be known. This work assumes that the reemission is related to the incident flux distribution by
![]() would be described by
would be described by
![]() is usually described by the relation
is usually described by the relation
![]() denotes ions and
denotes ions and
![]() denotes a sputtered particle type for which the kinetic energy can be neglected and a cosine-like directional distribution can be assumed, the reemission probability function takes the form [60]
denotes a sputtered particle type for which the kinetic energy can be neglected and a cosine-like directional distribution can be assumed, the reemission probability function takes the form [60]