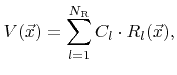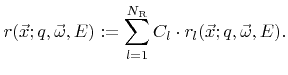2.3.1 Linear Surface Reactions

In many models the surface velocity is simply written as a linear function of rates

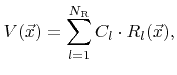$${V}({\vec{x}}) = \sum_{l=1}^{{{N}_\text{R}}}{C}_l\cdot{R}_l({\vec{x}}),$$ (2.28)

where 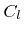${C}_l$ are constant coefficients. If this is the case, the individual contributions can be combined into a single rate 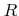${R}$ which is obtained by taking the superposition of all weight functions 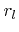${r}_l$ as the new weight function

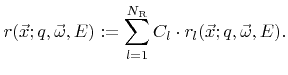$${r}({\vec{x}};{q},{\vec{\omega}},{E}) := \sum_{l=1}^{{{N}_\text{R}}} {C}_l\cdot{r}_l({\vec{x}};{q},{\vec{\omega}},{E}).$$ (2.29)

The surface velocity can then be written as

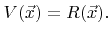$${V}({\vec{x}})={R}({\vec{x}}).$$ (2.30)

Simple deposition and etching models often assume such a linear surface reaction. If only a single particle species dominates the surface reaction, the surface velocity is typically modeled as

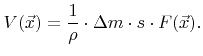$${V}({\vec{x}})=\frac{1}{{\rho}}\cdot\Delta{m}\cdot{s}\cdot{F}({\vec{x}}).$$ (2.31)

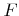Here ${F}$ is the total incident flux of particles, 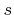${s}$ is the sticking or reaction probability, 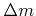$\Delta{m}$ is the mass which is deposited ( 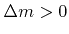$\Delta{m}>0$ ) or removed ( 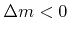$\Delta{m}<0$ ) from the surface per reacting incident particle, and 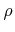${\rho}$ is the bulk density [91]. Advanced models use multiple particle types. For example, a linear model for TEOS deposition is given in [51]. There, different reaction paths are assumed. TEOS is modeled to be either deposited directly with a small sticking coefficient or through deposition of a very reactive intermediate with a large sticking coefficient, that is formed by gas phase reactions. Linear surface reactions are also used for some simple etching models, which require the incorporation of physical etching (sputtering) as well as chemical etching. If the two components are independent from each other, the reaction can be described by (2.28) [91].

Processes operating in the transport-controlled regime, which means that the particle transport to the surface is the crucial limiting factor for the surface velocity, can often be described by linear reaction models. There the surface velocity is essentially proportional to the particle transport to the surface.