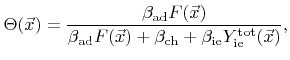2.3.2 Non-Linear Surface Reactions

In general, the surface velocity (2.25) is not a linear function. As an example, the sticking probability in (2.31) can depend on the local arriving particle flux, if higher order surface kinetics are assumed [21]

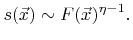$${s}({\vec{x}})\sim{F}({\vec{x}})^{{\eta}-1}.$$ (2.32)

Here 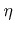${\eta }$ is the order of the reaction. Obviously, in the case of non-linear reaction kinetics ( 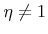${\eta}\neq1$ ) the sticking coefficient depends on the flux.

Other examples, where non-linear surface reactions need to be incorporated, are processes with ion-enhanced etching. There physical (ions) and chemical (neutrals) components act in a synergistic manner, so that the etch rate is larger than that obtained by summing up their individual contributions.

The Langmuir adsorption model is able to capture this behavior [91]. The idea is to assume an absorbed state of byproducts. The fraction of surface sites covered by these byproducts is called the surface coverage 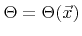${\Theta}={\Theta}({\vec{x}})$ . The etch rate is then composed of three contributions

$${V}({\vec{x}}) = \underbrace{-\alpha_{\text{ch}}\cdot{\Theta}({\v... ...})\cdot{Y}^{\text{tot}}_{\text{ie}}({\vec{x}})}_{\text{ion-enhanced etching}} .$$ (2.33)

The first term corresponds to chemical etching which is proportional to the coverage, the second term represents physical sputtering with the total sputter rate 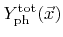${Y}^{\text{tot}}_{\text{ph}}({\vec{x}})$ , and the last term is due to ion-enhanced etching, which is proportional to the coverage and the total ion-enhanced etching rate 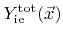${Y}^{\text{tot}}_{\text{ie}}({\vec{x}})$ . The total yields are both calculated using a weight function similar to that used in (2.27). Two different total yields are introduced, since in the general case the physical sputter yield and the ion-enhanced etching yield are not equal. 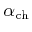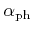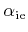The constants $\alpha_{\text{ch}}$ , $\alpha_{\text{ph}}$ , and $\alpha_{\text{ie}}$ in (2.33) are model parameters.

For the coverage 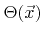${\Theta}({\vec{x}})$ a balanced equation can be set up as follows

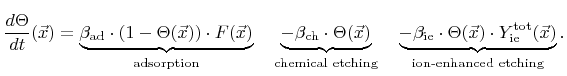$$\frac{{d}{\Theta}}{{d}{t}}({\vec{x}}) = \underbrace{\beta_{\text{... ...}})\cdot{Y}^{\text{tot}}_{\text{ie}}({\vec{x}})}_{\text{ion-enhanced etching}}.$$ (2.34)

The first term describes the adsorption of chemical components, which is proportional to the total arriving flux 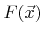${F}({\vec{x}})$ of neutrals and the fraction of empty surface sites 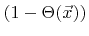$\left(1-{\Theta}({\vec{x}})\right)$ . The second and the third term are losses due to chemical and ion-enhanced etching, respectively, which are both proportional to the coverage. 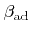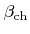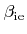The constants $\beta_{\text{ad}}$ , $\beta_{\text{ch}}$ , and $\beta_{\text{ie}}$ are again model parameters.

A common approach is to assume that the coverage is always in a steady state 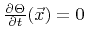$\frac{\partial{\Theta}}{\partial{t}}({\vec{x}})=0$ . Therefore, the coverage can be explicitly expressed as a function of the rates 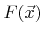${F}({\vec{x}})$ and ${Y}^{\text{tot}}_{\text{ie}}({\vec{x}})$ ,

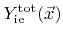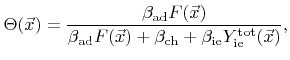$${\Theta}({\vec{x}})= \frac{ \beta_{\text{ad}}{F}({\vec{x}}) }{ \b... ...)+\beta_{\text{ch}}+\beta_{\text{ie}}{Y}^{\text{tot}}_{\text{ie}}({\vec{x}}) },$$ (2.35)

and can be plugged into (2.33). The result is a non-linear function of the rates for the surface velocity.