



Next: 4.3.3 Dilation
Up: 4.3 Sparse Field Implementation
Previous: 4.3.1 Time Integration
4.3.2 Pruning and Consistency Check
So far the H-RLE data structure contains the updated LS values
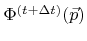 for all grid points from the active layer
for all grid points from the active layer
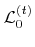 . As described in Section 3.4.2 a pruning procedure is necessary to avoid dense sets of active grid points. Again, a stencil of iterators, similar to that required for the computation of first order finite differences, is moved over the data structure. At the same time a new H-RLE data structure is set up in which all changes are stored. The new H-RLE data structure is constructed by copying the old one, while skipping defined grid points which do not have an opposite signed neighbor. These grid points are added to undefined runs instead.
. As described in Section 3.4.2 a pruning procedure is necessary to avoid dense sets of active grid points. Again, a stencil of iterators, similar to that required for the computation of first order finite differences, is moved over the data structure. At the same time a new H-RLE data structure is set up in which all changes are stored. The new H-RLE data structure is constructed by copying the old one, while skipping defined grid points which do not have an opposite signed neighbor. These grid points are added to undefined runs instead.
Since the neighbors of active grid points (belonging to
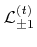 ) have not been updated yet, this early pruning procedure works only if the signs of non-active grid points (
) have not been updated yet, this early pruning procedure works only if the signs of non-active grid points (
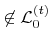 ) are not altered during the entire time integration step. According to Section 3.4.2 the signs of non-active grid points are maintained, if the CFL number
) are not altered during the entire time integration step. According to Section 3.4.2 the signs of non-active grid points are maintained, if the CFL number
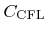 fulfills
fulfills
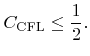 |
(4.8) |
As a consequence, the presented implementation of the sparse field method only allows CFL numbers satisfying this condition.
Before a defined grid point is inserted into the new H-RLE data structure, it is first checked, if its LS value is greater than
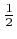 or smaller than
or smaller than
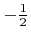 , while that of any neighboring defined grid point is less than
, while that of any neighboring defined grid point is less than
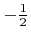 or larger than
or larger than
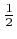 , respectively. If this is the case, the prerequisite of the sparse field LS method (3.27) would be violated. To guarantee the robustness of the algorithm the LS value must be reduced to
, respectively. If this is the case, the prerequisite of the sparse field LS method (3.27) would be violated. To guarantee the robustness of the algorithm the LS value must be reduced to
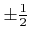 (while keeping its sign) before insertion into the new H-RLE data structure. After completing the iteration over the old H-RLE data structure and finishing the setup of the new one, the old H-RLE data structure can be deleted.
(while keeping its sign) before insertion into the new H-RLE data structure. After completing the iteration over the old H-RLE data structure and finishing the setup of the new one, the old H-RLE data structure can be deleted.




Next: 4.3.3 Dilation
Up: 4.3 Sparse Field Implementation
Previous: 4.3.1 Time Integration
Otmar Ertl: Numerical Methods for Topography Simulation
![]() ) have not been updated yet, this early pruning procedure works only if the signs of non-active grid points (
) have not been updated yet, this early pruning procedure works only if the signs of non-active grid points (
![]() ) are not altered during the entire time integration step. According to Section 3.4.2 the signs of non-active grid points are maintained, if the CFL number
) are not altered during the entire time integration step. According to Section 3.4.2 the signs of non-active grid points are maintained, if the CFL number
![]() fulfills
fulfills
![]() or smaller than
or smaller than
![]() , while that of any neighboring defined grid point is less than
, while that of any neighboring defined grid point is less than
![]() or larger than
or larger than
![]() , respectively. If this is the case, the prerequisite of the sparse field LS method (3.27) would be violated. To guarantee the robustness of the algorithm the LS value must be reduced to
, respectively. If this is the case, the prerequisite of the sparse field LS method (3.27) would be violated. To guarantee the robustness of the algorithm the LS value must be reduced to
![]() (while keeping its sign) before insertion into the new H-RLE data structure. After completing the iteration over the old H-RLE data structure and finishing the setup of the new one, the old H-RLE data structure can be deleted.
(while keeping its sign) before insertion into the new H-RLE data structure. After completing the iteration over the old H-RLE data structure and finishing the setup of the new one, the old H-RLE data structure can be deleted.