To extend the set of defined grid points on the positive and the negative side by a single layer, a stencil of iterators, which allows access to neighbor points, is moved over the H-RLE data structure. If any iterator from the stencil encounters a defined grid point, a defined grid point is inserted into the new H-RLE data structure. If the position of the central iterator represents a defined grid point, its LS value is simply copied. Otherwise, the LS value must be determined using the update scheme (3.29) and the LS values of neighbor points, which can be accessed by the non-central iterators. Here, positive and negative undefined runs are regarded to have LS values ![]() or
or ![]() , respectively. Since at least one iterator is at the position of a defined grid point the LS value of the newly inserted grid point is always defined. After completing the iteration, the old H-RLE data structure can be deleted. The new H-RLE data structure now contains all previously defined grid points along with the newly added defined grid points.
, respectively. Since at least one iterator is at the position of a defined grid point the LS value of the newly inserted grid point is always defined. After completing the iteration, the old H-RLE data structure can be deleted. The new H-RLE data structure now contains all previously defined grid points along with the newly added defined grid points.
After the first application of the dilation procedure, the LS values of all grid points in layers
![]() are updated. Since the CFL condition (3.31) implies that
are updated. Since the CFL condition (3.31) implies that
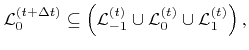 |
(4.9) |
However, this procedure also adds defined grid points to the H-RLE data structure, which are not really needed for the finite difference scheme. If
![]() additional layers are necessary, the last iteration which updates all points of layers
additional layers are necessary, the last iteration which updates all points of layers
![]() also adds some new points which are actually members of
also adds some new points which are actually members of
![]() . The insertion of these grid points can easily be avoided according to (3.26), if only grid points for which the new LS value fulfills
. The insertion of these grid points can easily be avoided according to (3.26), if only grid points for which the new LS value fulfills
![]() are added. The procedure can be further optimized by inserting new grid points as late as possible to speed up successive iterations over the H-RLE data structure. It is favorable to add only defined grid points with an absolute LS value not larger than
are added. The procedure can be further optimized by inserting new grid points as late as possible to speed up successive iterations over the H-RLE data structure. It is favorable to add only defined grid points with an absolute LS value not larger than
![]() during the
during the ![]() -th iteration.
-th iteration.
The dilation procedure scales with
![]() , where
, where
![]() is the number of defined grid points before dilation and
is the number of defined grid points before dilation and
![]() is the number of added layers. Hence, this algorithm is only efficient for small
is the number of added layers. Hence, this algorithm is only efficient for small
![]() , which is the case, if first (
, which is the case, if first (
![]() ) or second order finite difference schemes (
) or second order finite difference schemes (
![]() ) are used. For larger
) are used. For larger
![]() , an algorithm similar to the fast marching method [109] could probably be the better choice. However, this technique would require random access to the H-RLE data structure resulting in a non-linear performance with respect to
, an algorithm similar to the fast marching method [109] could probably be the better choice. However, this technique would require random access to the H-RLE data structure resulting in a non-linear performance with respect to
![]() .
.
The pruning and consistency check, as described in the previous section, can be included during the first dilation cycle. This avoids an iteration over the H-RLE data structure and accelerates the sparse field method.