



Next: 6.4 Volume Tetrahedralization
Up: 6. Architecture and Implementation
Previous: 6.2 Initial Point Generation
6.3 Surface Triangulation
Given a set of constraining input facets 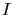 (polygonal representation,
Fig. 6.11) a surface triangulation is derived. All polygons are
triangulated by a recursive splitting algorithm. The polygons may be
non-convex, more than two polygons may share an edge, and they do not have
to form a closed surface.
Depending on the choice of mesh and discretization a refinement algorithm
is further applied to either enforce the smallest sphere or the Delaunay
criteria (Crit. 5.1, Crit. 5.2,
Crit. 3.1, and Crit. 3.2).
An important operation is defined to reduce the number of refinement
points.
(polygonal representation,
Fig. 6.11) a surface triangulation is derived. All polygons are
triangulated by a recursive splitting algorithm. The polygons may be
non-convex, more than two polygons may share an edge, and they do not have
to form a closed surface.
Depending on the choice of mesh and discretization a refinement algorithm
is further applied to either enforce the smallest sphere or the Delaunay
criteria (Crit. 5.1, Crit. 5.2,
Crit. 3.1, and Crit. 3.2).
An important operation is defined to reduce the number of refinement
points.
The term flip saturation is introduced.
A triangle may not satisfy the smallest sphere criterion and may
not be flip-able. The triangle may become flip-able after a certain number of
flip operations are applied on other triangles (Fig. 6.4).
This situation is said to be unsaturated. It is desired to reach
the state of flip saturation before unnecessary refinement occurs.
This is achieved by employing the recursive triangle flip.
Figure 6.4:
A triangle which is at first not flip-able and the state of flip
saturation.
|
|
- Recursive Triangle Flip
-
Two triangles 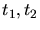 are flipped. The resulting triangles
are flipped. The resulting triangles 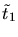 and
and
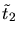 are each checked if they are flip-able. If any of
the two triangles
are each checked if they are flip-able. If any of
the two triangles
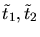 is flip-able with
a triangle
is flip-able with
a triangle 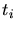 where
where 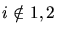 it will be flipped as
well. Repeat for the flipped triangle
it will be flipped as
well. Repeat for the flipped triangle 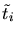 until no
further flip operations are possible.
until no
further flip operations are possible.
This operation is performed once on each triangle during a linear scan
over all existing triangles. The procedure during which no refinement is
allowed is only necessary at the start to ensure flip saturation.
Afterwards, during refinement the flip saturation is maintained after
insertion of a point by applying the recursive flip locally on the
affected triangle only.
It follows a definition of structural and flip-able edges.
An example of an edge shared by more than two triangles is shown in
Fig. 6.5.
Figure 6.5:
Multiple connected edges.
|
|
Edges with only one adjacent facet are structural and a potential
inconsistency. They may indicate an undesired gap in the surface
representation. The current implementation allows to repair such faults by
tracing these edges and linking them to construct a three-dimensional ring.
If this ring consists of a large number of edges, it can be assumed that the
boundary does not form a closed surface intentionally and no action will be
taken. On the other hand if the ring is relatively small, it can be assumed
that a hole in the surface has been detected. The hole can be patched by
a non-planar triangulation of the ring. This is performed by the general
polygon triangulation algorithm which was used for the facets of the
input 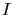 .
.
Note that two triangles need not be flip-able if they share a
flip-able edge (Fig. 6.6).
Figure 6.6:
Non-convex coplanar triangles. The common edge is
by definition flip-able, while the triangles are not.
|
|
All S-edges are detected and stored in a special data
structure for further processing. The smallest sphere criterion
will be enforced for S-edges by a novel refinement scheme
presented in this section (Fig. 6.7).
The idea is to avoid overrefinement due to a feedback situation
where an inserted point causes further point insertions for other
S-edges. This is especially important when incident
S-edges span angles of less than 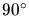 .
The S-edges are drawn in bold, the dashed circles illustrate
the minimal edge length up to which refinement is permitted, and the
solid circles symbolize sphere tests.
There are two possible types how a refinement point is derived from
points which inflict the sphere criterion. Such points will be called
disturbing points.
.
The S-edges are drawn in bold, the dashed circles illustrate
the minimal edge length up to which refinement is permitted, and the
solid circles symbolize sphere tests.
There are two possible types how a refinement point is derived from
points which inflict the sphere criterion. Such points will be called
disturbing points.
- Type P Insertion
- An orthogonal projection of the disturbing
point onto the S-edge is used.
- Type R Insertion
- The disturbing point is rotated onto the
S-edge. The rotation axis passes through the point at which
the two S-edges are incident.
If more than one disturbing point exists, a best candidate is selected
by comparing the relative distance and choosing the closest.
The simple cases are P I and R I. In P II, R II, and
R IV the minimal edge length is limited and the inserted point
receives an offset. If the ratio between the length of the two
S-edges is close to one, the most complex situation case
R III evolves. An offset as in case R IV would not
produce a good result and the sphere test depicted by the left solid
circle in case R IV could fail due to the inserted point.
An overall improved situation results from an intended first order
feedback where actually two points will be inserted in two consecutive
steps R III + R I.
The circle for the sphere test which causes the insertion in the first
place is omitted in all sketches. Once the location of the new point
has been determined and prior to its insertion, sphere tests are
performed for some of the new edges to avoid feedback (solid circles).
Figure 6.7:
Refinement types for structural edges.
|
|
Figure 6.8:
Refining structural edges for the trivial case of a
planar polygon.
|
|
Note that the algorithm is designed for three dimensions in spite of
the two-dimensional sketches. Figure 6.8 shows the result for
the trivial case of a planar polygon. The S-edges (outline) satisfy
the smallest sphere criterion after refinement.
The triangles are processed after the S-edges. If desirable, the
refinement can be reduced by omitting the smallest sphere criterion for
triangles (Crit. 3.1).
The weaker Delaunay criterion (Crit. 5.2) cannot be checked
easily, because the number of spheres to test can theoretically be
infinite as the criterion requires a sphere of any size to be empty.
Hence, the insphere test would have to be repeated for different
sizes until an empty sphere has been found.
An equivalent criterion was devised which needs at most two insphere tests.
It uses a metric 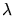 which will be described later on in
Section 6.4.
which will be described later on in
Section 6.4.
A non-Delaunay triangle and a Delaunay triangle with two disturbing points
located inside of the smallest sphere and the empty double sphere are
depicted in Fig. 6.9.
Figure 6.9:
Double sphere criterion.
|
|
A key idea for Steiner point refinement with provable bounds was discussed
in Section 5.6.
The circumcenter of a triangle is a very well suited location for a new
point to be inserted.
The triangle which will actually be split can be different from the
triangle which causes the refinement. Hence, a triangle search by e.g. a
jump and walk algorithm is required.
An algorithm was implemented which extends this concept for non-planar
surfaces (Fig. 6.10).
Figure 6.10:
Locating the triangle which contains the projection of the
circumcenter and flipping of the non-structural edge.
|
|
The location of the new point  is derived from the circumcenter
is derived from the circumcenter 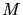 by an orthogonal projection.
by an orthogonal projection. 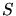 is the point
is the point 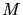 projected onto
the surface (
projected onto
the surface ( 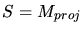 ). It is checked if the refinement
point
). It is checked if the refinement
point 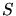 really violates the sphere criterion of the bad triangle.
The point
really violates the sphere criterion of the bad triangle.
The point 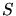 might fall outside of the sphere in which case a Steiner
point refinement would not be justified, because the bad triangle would
survive the Delaunay update step.
A point location is necessary to find the triangle containing
might fall outside of the sphere in which case a Steiner
point refinement would not be justified, because the bad triangle would
survive the Delaunay update step.
A point location is necessary to find the triangle containing 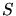 for a
given
for a
given 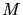 . The direction of projection is orthogonal to the plane spanned
by the bad triangle. The triangle search can be performed by a
walk algorithm.
. The direction of projection is orthogonal to the plane spanned
by the bad triangle. The triangle search can be performed by a
walk algorithm.
- Locate Triangle
-
Starting with a triangle 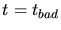 and a given point
and a given point 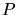 a triangle
is searched for which contains
a triangle
is searched for which contains 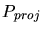 . (Usually
. (Usually 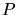 is the
circumcenter
is the
circumcenter 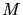 .) The direction of projection is defined by the normal
vector
.) The direction of projection is defined by the normal
vector 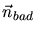 of
of 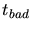 .
An edge
.
An edge 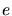 of
of 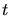 and
and 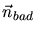 define a plane which separates two
half spaces. The edge
define a plane which separates two
half spaces. The edge 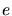 is said to face the point
is said to face the point 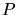 ,
if
,
if 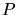 and
and 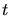 do not lie in the same half space.
Determine one edge
do not lie in the same half space.
Determine one edge 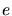 of
of 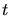 which faces
which faces 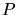 and which is a flip-able edge
(Def. 6.2). Follow edge
and which is a flip-able edge
(Def. 6.2). Follow edge 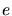 by finding the adjacent triangle
by finding the adjacent triangle
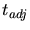 . Repeat for
. Repeat for 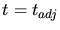 until an S-edge has been
encountered or until the triangle
until an S-edge has been
encountered or until the triangle 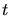 possesses no edge
possesses no edge 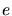 which faces
which faces 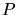 .
In either case the search is terminates. In the latter case
.
In either case the search is terminates. In the latter case 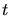 contains
contains 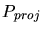 . The Steiner point
. The Steiner point 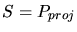 on
on  is
calculated by intersecting the found triangle
is
calculated by intersecting the found triangle  with the line defined
by
with the line defined
by 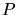 and the direction of projection.
and the direction of projection.
The point 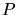 was used in the description to show that the algorithm can
search for arbitrary points where
was used in the description to show that the algorithm can
search for arbitrary points where 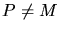 . This is important when
Steiner points are derived from disturbing points instead of circumcenters.
. This is important when
Steiner points are derived from disturbing points instead of circumcenters.
If the triangle is not extremely obtuse, 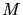 will be
contained in the triangle itself or in an adjacent triangle. Then,
no iterations or only a few will be required.
If an S-edge is encountered the triangle will not be refined.
Instead the S-edge will be refined as described above.
This is important for several reasons. Insertion of
will be
contained in the triangle itself or in an adjacent triangle. Then,
no iterations or only a few will be required.
If an S-edge is encountered the triangle will not be refined.
Instead the S-edge will be refined as described above.
This is important for several reasons. Insertion of 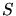 is
usually followed by triangle flip operations which eliminate the bad
triangle. Hence, the edge to follow must be flip-able.
Also, it is of limited sense to project
is
usually followed by triangle flip operations which eliminate the bad
triangle. Hence, the edge to follow must be flip-able.
Also, it is of limited sense to project 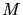 onto the surface for regions
with sharp dihedral angles.
onto the surface for regions
with sharp dihedral angles.
Originally, this type of refinement should only be applied to Delaunay
triangles with an empty circumsphere to improve quality angle
criteria. If the circumsphere is not empty, points could be inserted
too close to each other. In the present case this is not necessary.
In fact the Steiner point refinement of non-Delaunay triangles
proves successful for enforcing the Delaunay criterion as long as the state
of flip saturation is guaranteed and maintained after each point insertion.
At the same time it is possible to define minimum angle and maximum area
criteria upon which Delaunay surface triangles are adapted by the insertion of
Steiner points. These can be applied inhomogeneously according to a control
function. For the example in Fig. 6.11 the structural edges are
shown in Fig. 6.12, the Delaunay surface triangulation in
Fig. 6.13, and the adapted surface mesh in Fig. 6.14.
Figure 6.11:
Polygonal boundary description of a MOS Transistor with a
spacer.
|
|
Figure 6.12:
Structural edges of the MOS transistor example.
|
|
Figure 6.13:
Delaunay surface triangulation.
|
|
Figure 6.14:
Adapted surface mesh after Steiner point insertions.
|
|




Next: 6.4 Volume Tetrahedralization
Up: 6. Architecture and Implementation
Previous: 6.2 Initial Point Generation
Peter Fleischmann
2000-01-20
![]() (polygonal representation,
Fig. 6.11) a surface triangulation is derived. All polygons are
triangulated by a recursive splitting algorithm. The polygons may be
non-convex, more than two polygons may share an edge, and they do not have
to form a closed surface.
Depending on the choice of mesh and discretization a refinement algorithm
is further applied to either enforce the smallest sphere or the Delaunay
criteria (Crit. 5.1, Crit. 5.2,
Crit. 3.1, and Crit. 3.2).
An important operation is defined to reduce the number of refinement
points.
(polygonal representation,
Fig. 6.11) a surface triangulation is derived. All polygons are
triangulated by a recursive splitting algorithm. The polygons may be
non-convex, more than two polygons may share an edge, and they do not have
to form a closed surface.
Depending on the choice of mesh and discretization a refinement algorithm
is further applied to either enforce the smallest sphere or the Delaunay
criteria (Crit. 5.1, Crit. 5.2,
Crit. 3.1, and Crit. 3.2).
An important operation is defined to reduce the number of refinement
points.
![\includegraphics [height=4cm]{ppl/notflipable.ps}](img277.gif)
![]() .
The S-edges are drawn in bold, the dashed circles illustrate
the minimal edge length up to which refinement is permitted, and the
solid circles symbolize sphere tests.
There are two possible types how a refinement point is derived from
points which inflict the sphere criterion. Such points will be called
disturbing points.
.
The S-edges are drawn in bold, the dashed circles illustrate
the minimal edge length up to which refinement is permitted, and the
solid circles symbolize sphere tests.
There are two possible types how a refinement point is derived from
points which inflict the sphere criterion. Such points will be called
disturbing points.
![]() which will be described later on in
Section 6.4.
which will be described later on in
Section 6.4.
![\includegraphics [width=0.36\textwidth]{ppl/steiner25d.eps}](img285.gif)
![]() will be
contained in the triangle itself or in an adjacent triangle. Then,
no iterations or only a few will be required.
If an S-edge is encountered the triangle will not be refined.
Instead the S-edge will be refined as described above.
This is important for several reasons. Insertion of
will be
contained in the triangle itself or in an adjacent triangle. Then,
no iterations or only a few will be required.
If an S-edge is encountered the triangle will not be refined.
Instead the S-edge will be refined as described above.
This is important for several reasons. Insertion of ![]() is
usually followed by triangle flip operations which eliminate the bad
triangle. Hence, the edge to follow must be flip-able.
Also, it is of limited sense to project
is
usually followed by triangle flip operations which eliminate the bad
triangle. Hence, the edge to follow must be flip-able.
Also, it is of limited sense to project ![]() onto the surface for regions
with sharp dihedral angles.
onto the surface for regions
with sharp dihedral angles.