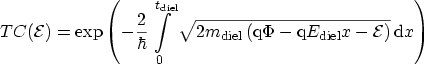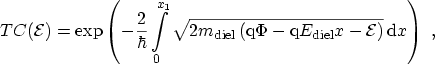3.5.1 The WENTZEL-KRAMERS-BRILLOUIN Approximation
The WENTZEL-KRAMERS-BRILLOUIN3.6 (WKB) approximation is one of the most
frequently encountered assumptions for the quantum-mechanical wave
function. It is often used for tunneling simulations and has been implemented
in device simulators [128,129,96]. Within the WKB
approximation, the transmission coefficient can be written as (for a detailed
derivation see Appendix B) [130,131]
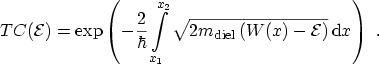 |
(3.55) |
In this expression the integration is performed only within the classical
turning points 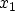 and
and 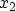 , defined by the region where
, defined by the region where
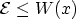 and the integrand in (3.55) is real. Thus, only the
decaying part of the wave function is considered. For a linear energy barrier
the numerical calculation of the integral in (3.55) can be
avoided. Still, it is necessary to distinguish between regions where
direct or FOWLER-NORDHEIM tunneling takes
place. For the direct tunneling regime
and the integrand in (3.55) is real. Thus, only the
decaying part of the wave function is considered. For a linear energy barrier
the numerical calculation of the integral in (3.55) can be
avoided. Still, it is necessary to distinguish between regions where
direct or FOWLER-NORDHEIM tunneling takes
place. For the direct tunneling regime
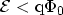 holds
(see Fig. 3.9). Therefore, the transmission coefficient
holds
(see Fig. 3.9). Therefore, the transmission coefficient
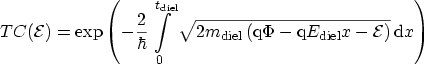 |
(3.56) |
evaluates to
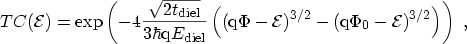 |
(3.57) |
with
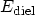 being the electric field defined as
being the electric field defined as
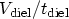 and
and
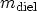 the electron
mass in the dielectric. The symbols
the electron
mass in the dielectric. The symbols 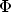 and
and 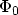 denote the upper and lower
barrier heights, as shown in Fig. 3.9. The value of
denote the upper and lower
barrier heights, as shown in Fig. 3.9. The value of 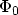 is calculated
assuming a linear potential in the barrier
is calculated
assuming a linear potential in the barrier
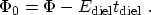 |
(3.58) |
For the FOWLER-NORDHEIM tunneling regime it holds
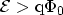 and therefore with
and therefore with
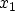 defined by
defined by
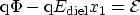 the transmission coefficient
the transmission coefficient
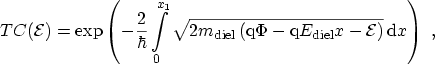 |
(3.59) |
evaluates to
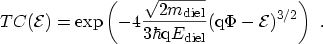 |
(3.60) |
The WKB tunneling coefficient is frequently multiplied by an oscillating
prefactor to reproduce FOWLER-NORDHEIM-induced
oscillations [132,133,134,135,136]. However, since
no wave function interference is taken into account, the general validity of
this method is questionable.
A. Gehring: Simulation of Tunneling in Semiconductor Devices