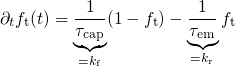
The trapping dynamics in the simplest case are governed by the first-order rate equation
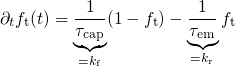 | (4.1) |
with 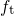 being the electron occupancy of a single trap. Each of these traps is
characterized by its own capture (
being the electron occupancy of a single trap. Each of these traps is
characterized by its own capture (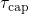 ) and emission (
) and emission (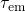 ) time constant, which
are related to the forward (
) time constant, which
are related to the forward (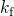 ) or the reverse (
) or the reverse (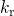 ) rate, respectively. The first term
on the right-hand side of equation (4.1) has a positive sign, stands for electron
trapping and increases
) rate, respectively. The first term
on the right-hand side of equation (4.1) has a positive sign, stands for electron
trapping and increases 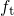 . By contrast, detrapping is represented by the second
term with the negative sign and causes a reduction in
. By contrast, detrapping is represented by the second
term with the negative sign and causes a reduction in 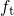 . It is emphasized that the
defects have only discrete occupation numbers. This means that the defects carry
an integer number of electrons and thus
. It is emphasized that the
defects have only discrete occupation numbers. This means that the defects carry
an integer number of electrons and thus 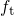 must equal to either zero or
unity. However, for a large number of defects,
must equal to either zero or
unity. However, for a large number of defects, 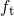 corresponds to the average
occupation number and thus takes values within the range
corresponds to the average
occupation number and thus takes values within the range ![[0,1]](diss1569x.png) . It is further
mentioned that the physical trapping process is of a stochastic nature, as it
has also been the case for electron tunneling and vibronic transitions in
Chapter 2. These stochastic processes are characterized by the fact that the
transition times are statistically distributed. As a consequence,
. It is further
mentioned that the physical trapping process is of a stochastic nature, as it
has also been the case for electron tunneling and vibronic transitions in
Chapter 2. These stochastic processes are characterized by the fact that the
transition times are statistically distributed. As a consequence, 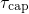 and
and 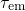 correspond to the expectation value of the capture (
correspond to the expectation value of the capture (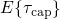 ) or emission
(
) or emission
(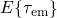 ) times, respectively, and the electron occupancy only changes gradually
with time. The electron occupancy as a function of time is determined by
the rate equation (4.1), which is a first-order differential equation with the
solution
) times, respectively, and the electron occupancy only changes gradually
with time. The electron occupancy as a function of time is determined by
the rate equation (4.1), which is a first-order differential equation with the
solution
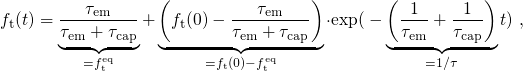 | (4.2) |
and is depicted in Fig. 4.1. The first term of equation (4.2) corresponds to the
equilibrium occupancy 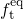 , which approaches unity for the assumption
, which approaches unity for the assumption
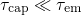 . The second term describes an exponential transition of
. The second term describes an exponential transition of 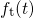 towards
towards
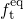 . In a time-logarithmic representation this leads to a step of
. In a time-logarithmic representation this leads to a step of 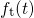 , occurring
within three decades around
, occurring
within three decades around  . This step is associated with the expectation value of
the transition
. This step is associated with the expectation value of
the transition 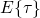 in the trapping process and the stochastic nature of this
process is reflected in the washed-out shape of the step. As demonstrated in Fig. 4.1,
the step linearly shifts with the order of magnitude of
in the trapping process and the stochastic nature of this
process is reflected in the washed-out shape of the step. As demonstrated in Fig. 4.1,
the step linearly shifts with the order of magnitude of  . Furthermore, its height
reaches the maximal value of
. Furthermore, its height
reaches the maximal value of 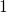 when the capture and emission time constant
differ by some orders of magnitude. Note that hole detrapping requires that
when the capture and emission time constant
differ by some orders of magnitude. Note that hole detrapping requires that
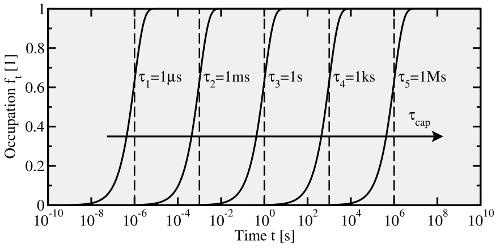
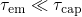 and the time point of the transition is then determined by
and the time point of the transition is then determined by
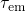 .
.
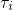 assuming
assuming 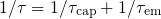 and
and
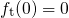 .
. 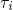 gives the time point, when the trapping process should occur
according to its expectation value
gives the time point, when the trapping process should occur
according to its expectation value 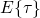 . In a time-logarithmic plot, the time
point of the transition shifts linearly with the order of magnitude of
. In a time-logarithmic plot, the time
point of the transition shifts linearly with the order of magnitude of 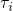 .
.One has to consider that the atomic structure of defects strongly influences the defect
properties. Dielectric host materials, in particular 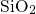 and
and 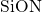 , exhibit an
amorphous structure with large variations in the bond lengths and angles, which are
assumed to have an impact on
, exhibit an
amorphous structure with large variations in the bond lengths and angles, which are
assumed to have an impact on 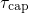 and
and 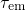 . As a result, the trapping time
constants in equation (4.1) are subject to a dispersion. This will be accounted
for by a probability density function
. As a result, the trapping time
constants in equation (4.1) are subject to a dispersion. This will be accounted
for by a probability density function 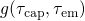 , which is normalized by
definition. Then the time evolution of trapped charges
, which is normalized by
definition. Then the time evolution of trapped charges 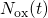 can be expressed
as
can be expressed
as
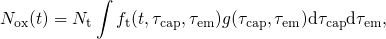 | (4.3) |
where 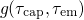 is normalized and
is normalized and 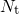 stands for the concentration of traps. The
integral in equation (4.3) can be interpreted as a superposition of individual and thus
independent trapping processes. Note that this concept is in agreement with the
findings of TDDS, in which the single trapping processes take place almost
independently from each other.
stands for the concentration of traps. The
integral in equation (4.3) can be interpreted as a superposition of individual and thus
independent trapping processes. Note that this concept is in agreement with the
findings of TDDS, in which the single trapping processes take place almost
independently from each other.
In a phenomenological model of Yang et al. [58], the capture and emission time constants were correlated by the relation
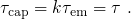 | (4.4) |
Furthermore, Yang et al. assumed a log-normal distribution of 
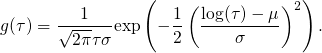 | (4.5) |
Although his model allows reasonable fits to single relaxation curves, it is inconsistent with the scalability of the experimental data (see Section 1.4). This is due to the fact that neither the probability density function nor the time constants have a field- or temperature dependence, which were not considered. Nevertheless, the above formulation of the rates already includes the central aspects of a charge trapping model and thus has served as a foundation for other models. The following points are suggested as an improvement for Yang’s model:
 .
.
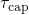 and
and 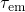 are sought, which are derived
from physical considerations and must consequently depend on the temperature
and the electrostatics in the device.
are sought, which are derived
from physical considerations and must consequently depend on the temperature
and the electrostatics in the device.