6.1 McWhorter Model
In the middle of the last century, McWhorter [182] dealt with the spectrum of
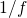 -noise observed at germanium-oxide interfaces. This kind of noise is attributed
to fluctuations in the trap occupancy
-noise observed at germanium-oxide interfaces. This kind of noise is attributed
to fluctuations in the trap occupancy 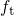 due to charge carriers tunneling forth
and back between the bulk and the defects. McWhorter described these
fluctuations using a simple SRH-based model, which can be considered as a
prototype for other charge trapping models. His model extends the conventional
SRH theory by the effect of charge carrier tunneling, which is accounted for
by the factor
due to charge carriers tunneling forth
and back between the bulk and the defects. McWhorter described these
fluctuations using a simple SRH-based model, which can be considered as a
prototype for other charge trapping models. His model extends the conventional
SRH theory by the effect of charge carrier tunneling, which is accounted for
by the factor 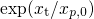 . Thus, the simplified time constants read as
. Thus, the simplified time constants read as
The model presumes that all traps are energetically located within the substrate
bandgap so that none of them will be found below 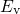 . Furthermore, they are
assumed to be spatially distributed over the entire dielectric.
. Furthermore, they are
assumed to be spatially distributed over the entire dielectric.
In the following, the McWhorter model will be evaluated against the findings of the
TDDS experiments (see Section 1.3.4).
- After equation (6.1)
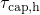 shows a weak field dependence following
shows a weak field dependence following 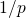 .
The drop in the hole concentration
.
The drop in the hole concentration 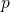 at small fields leads to a sharp
peak, which is inconsistent with the field acceleration observed in TDDS
experiments.
at small fields leads to a sharp
peak, which is inconsistent with the field acceleration observed in TDDS
experiments.
- Since the hole concentration weakly varies with changes in the
temperature, the hole capture process is not thermally activated.
- The field dependence of
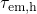 is governed by the exponential term
is governed by the exponential term
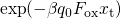 and thus is inconsistent with the behavior of ‘normal’
defects. But one should keep in mind that some RTN investigations [125,
55] have revealed that there exist defects whose emission times increase
exponentially with the gate bias.
and thus is inconsistent with the behavior of ‘normal’
defects. But one should keep in mind that some RTN investigations [125,
55] have revealed that there exist defects whose emission times increase
exponentially with the gate bias.
- Consequently, the McWhorther model does also not agree with the linear
dependence on
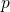 seen for
seen for 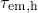 in the case of the ‘anomalous’ defects.
Beyond that, it does not give an explanation for the two distinct kinds of
defects in general.
in the case of the ‘anomalous’ defects.
Beyond that, it does not give an explanation for the two distinct kinds of
defects in general.
- The McWhorther model predicts
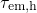 to be temperature-activated in
agreement with the experimental findings.
to be temperature-activated in
agreement with the experimental findings.
The term 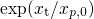 in
in 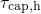 and
and 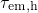 accounts for the trap depth
dependence of tunneling and leads to an upwards shift of the entire
accounts for the trap depth
dependence of tunneling and leads to an upwards shift of the entire 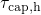 and
and
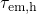 curves with an increasing trap depth
curves with an increasing trap depth 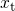 . Due to the wide distribution of
. Due to the wide distribution of 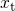 ,
the McWhorter model allows a wide range of capture and emission times in thick
oxides. In modern device technologies, however, the time constant of the
devices with an oxide thickness of
,
the McWhorter model allows a wide range of capture and emission times in thick
oxides. In modern device technologies, however, the time constant of the
devices with an oxide thickness of 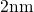 would be limited to
would be limited to 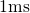 after
the model. As such, this model cannot explain time constants larger than
after
the model. As such, this model cannot explain time constants larger than
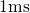 for devices with an oxide thickness of
for devices with an oxide thickness of 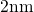 . This is in contrast to the
experimental results (cf. Fig. 1.2), in which
. This is in contrast to the
experimental results (cf. Fig. 1.2), in which 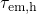 extends well into the
kilosecond regime. In conclusion, this model cannot be reconciled with the
findings of the TDDS and is thus inadequate to describe the traps involved in
NBTI.
extends well into the
kilosecond regime. In conclusion, this model cannot be reconciled with the
findings of the TDDS and is thus inadequate to describe the traps involved in
NBTI.
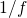 -noise observed at germanium-oxide interfaces. This kind of noise is attributed
to fluctuations in the trap occupancy
-noise observed at germanium-oxide interfaces. This kind of noise is attributed
to fluctuations in the trap occupancy 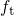 due to charge carriers tunneling forth
and back between the bulk and the defects. McWhorter described these
fluctuations using a simple SRH-based model, which can be considered as a
prototype for other charge trapping models. His model extends the conventional
SRH theory by the effect of charge carrier tunneling, which is accounted for
by the factor
due to charge carriers tunneling forth
and back between the bulk and the defects. McWhorter described these
fluctuations using a simple SRH-based model, which can be considered as a
prototype for other charge trapping models. His model extends the conventional
SRH theory by the effect of charge carrier tunneling, which is accounted for
by the factor 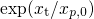 . Thus, the simplified time constants read as
. Thus, the simplified time constants read as
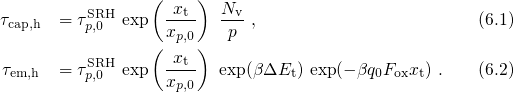
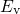 . Furthermore, they are
assumed to be spatially distributed over the entire dielectric.
. Furthermore, they are
assumed to be spatially distributed over the entire dielectric.
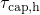 shows a weak field dependence following
shows a weak field dependence following 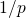 .
The drop in the hole concentration
.
The drop in the hole concentration 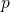 at small fields leads to a sharp
peak, which is inconsistent with the field acceleration observed in TDDS
experiments.
at small fields leads to a sharp
peak, which is inconsistent with the field acceleration observed in TDDS
experiments.
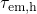 is governed by the exponential term
is governed by the exponential term
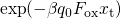 and thus is inconsistent with the behavior of ‘normal’
defects. But one should keep in mind that some RTN investigations
and thus is inconsistent with the behavior of ‘normal’
defects. But one should keep in mind that some RTN investigations 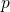 seen for
seen for 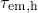 in the case of the ‘anomalous’ defects.
Beyond that, it does not give an explanation for the two distinct kinds of
defects in general.
in the case of the ‘anomalous’ defects.
Beyond that, it does not give an explanation for the two distinct kinds of
defects in general.
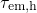 to be temperature-activated in
agreement with the experimental findings.
to be temperature-activated in
agreement with the experimental findings.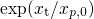 in
in 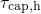 and
and 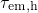 accounts for the trap depth
dependence of tunneling and leads to an upwards shift of the entire
accounts for the trap depth
dependence of tunneling and leads to an upwards shift of the entire 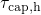 and
and
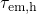 curves with an increasing trap depth
curves with an increasing trap depth 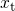 . Due to the wide distribution of
. Due to the wide distribution of 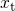 ,
the McWhorter model allows a wide range of capture and emission times in thick
oxides. In modern device technologies, however, the time constant of the
devices with an oxide thickness of
,
the McWhorter model allows a wide range of capture and emission times in thick
oxides. In modern device technologies, however, the time constant of the
devices with an oxide thickness of 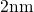 would be limited to
would be limited to 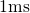 after
the model. As such, this model cannot explain time constants larger than
after
the model. As such, this model cannot explain time constants larger than
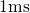 for devices with an oxide thickness of
for devices with an oxide thickness of 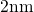 . This is in contrast to the
experimental results (cf. Fig.
. This is in contrast to the
experimental results (cf. Fig. 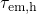 extends well into the
kilosecond regime. In conclusion, this model cannot be reconciled with the
findings of the TDDS and is thus inadequate to describe the traps involved in
NBTI.
extends well into the
kilosecond regime. In conclusion, this model cannot be reconciled with the
findings of the TDDS and is thus inadequate to describe the traps involved in
NBTI.