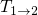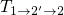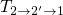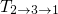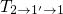7.6 Discussion
As demonstrated in great detail, the eNMP model successfully reproduces the
features of the time constants extracted from TDDS measurements. These
experiments reveal the behavior of single defects by monitoring the response of single
defects to different stressing conditions. This has made it possible to identify the
underlying physical process involved in charge trapping. Reisinger et al. [54]
established the link between single defects and NBTI by showing that the NBTI
degradation is primarily caused by a large number of individual trapping events.
The capture and emission times of these events are characterized by a wide
distribution. In the eNMP this can be explained by large variations in the
adiabatic potentials of defects, as usual for defects in an amorphous host
materials [20, 19]. Fig. 7.12 illustrates how single hole capture events sum up to
smooth degradation curves obtained in NBTI measurements. It becomes
clear that the increase in the number of traps leads to an averaging of the
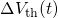 curves and the steps of single events cannot be resolved anymore.
The distribution of hole capture times determines the form of the stress
curves while the corresponding emission times yields the recovery curves.
Consequently, the field acceleration and temperature activation of the time
constants may explain the field and temperature dependences of the NBTI
degradation curves. But one should keep in mind that the permanent component
of NBTI is not captured by TDDS and thus have not been accounted for
in the eNMP model. As a result, a significant contribution to the overall
NBTI degradation is not described by the hole capture and emission process.
curves and the steps of single events cannot be resolved anymore.
The distribution of hole capture times determines the form of the stress
curves while the corresponding emission times yields the recovery curves.
Consequently, the field acceleration and temperature activation of the time
constants may explain the field and temperature dependences of the NBTI
degradation curves. But one should keep in mind that the permanent component
of NBTI is not captured by TDDS and thus have not been accounted for
in the eNMP model. As a result, a significant contribution to the overall
NBTI degradation is not described by the hole capture and emission process.
In the TSM the hole capture is modeled by an MPE process, which relies on a
concept similar to the charge transfer reactions in the eNMP model. In both cases,
the defect has to overcome an energy barrier resulting from the intersection of two
adiabatic potentials in the configuration coordinate diagram. While the height of this
barrier is a random variable in the TSM, it is determined from the shape of the
adiabatic potentials in the eNMP model. In the latter, the intersection point varies
with the relative position of the adiabatic potentials and consequently with the oxide
field. Together with the intermediate state  , which is involved in the hole
capture process, the eNMP model can reproduce the time constants seen
in TDDS. By contrast, a field enhancement factor in the TSM had to be
phenomenologically introduced in order to capture the field dependence
observed in the experimental data. For the aforementioned reasons, the eNMP
model is viewed as an improvement in the description of the hole capture
process.
, which is involved in the hole
capture process, the eNMP model can reproduce the time constants seen
in TDDS. By contrast, a field enhancement factor in the TSM had to be
phenomenologically introduced in order to capture the field dependence
observed in the experimental data. For the aforementioned reasons, the eNMP
model is viewed as an improvement in the description of the hole capture
process.
Apart from these physical details, the higher-level picture of the hole capture process
remains the same for both models. In the precursor configuration (state 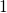 in both
models), the defect features a trap level located far below the substrate valence band.
Note that this level is referred to as
in both
models), the defect features a trap level located far below the substrate valence band.
Note that this level is referred to as 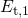 in the TSM or
in the TSM or 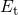 in the eNMP model. If
in the eNMP model. If
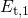 /
/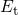 is shifted upwards by the oxide field, the defect can capture a substrate
hole. This is accompanied by a structural relaxation of the defect configuration and
leads to a new trap level
is shifted upwards by the oxide field, the defect can capture a substrate
hole. This is accompanied by a structural relaxation of the defect configuration and
leads to a new trap level 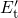 located within or at least close to the substrate
bandgap.
located within or at least close to the substrate
bandgap.
The TSM as well as the eNMP model can describe defects which show a field
dependence in the emission times and the recovery, respectively. This behavior is
linked to a hole emission process, which neutralizes the defect via the transition
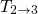 in the TSM or
in the TSM or 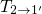 in the eNMP. As mentioned before, the corresponding
trap level is
in the eNMP. As mentioned before, the corresponding
trap level is 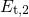 in the TSM and
in the TSM and 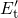 in the eNMP model and lies within or close
to the substrate bandgap. As a result, the occupation of
in the eNMP model and lies within or close
to the substrate bandgap. As a result, the occupation of 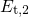 or
or 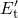 is
strongly dependent of small variations of the substrate Fermi level, also known
as the ‘switching trap’ behavior of defects. Only from the neutral charge
state (the state
is
strongly dependent of small variations of the substrate Fermi level, also known
as the ‘switching trap’ behavior of defects. Only from the neutral charge
state (the state 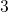 in the TSM and the state
in the TSM and the state 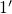 in the eNMP model), the
defect is allowed to return to its initial state
in the eNMP model), the
defect is allowed to return to its initial state 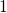 by structural relaxation. In
the state diagrams, the last step corresponds to the transition
by structural relaxation. In
the state diagrams, the last step corresponds to the transition 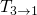 in
the TSM or
in
the TSM or 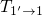 in the eNMP model. It is important to note here that
the hole emission times in both models are eventually controlled by the
position of
in the eNMP model. It is important to note here that
the hole emission times in both models are eventually controlled by the
position of 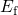 relative to
relative to 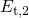 or
or 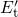 . This effect is reflected in the field
dependence of the ‘anomalous’ defects, on the one hand, and NBTI recovery,
on the other hand. Consider that the transition
. This effect is reflected in the field
dependence of the ‘anomalous’ defects, on the one hand, and NBTI recovery,
on the other hand. Consider that the transition 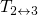 in the TSM and
in the TSM and
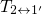 in the eNMP model are actually based on a different description of the
hole capture and emission process. However, the corresponding transition
barriers are assumed to be small in both models. Therefore,
in the eNMP model are actually based on a different description of the
hole capture and emission process. However, the corresponding transition
barriers are assumed to be small in both models. Therefore, 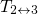 in the TSM
and
in the TSM
and 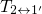 in the eNMP model occur fast so that the occupancies of the
involved states reach their equilibrium values, which are unaffected by the
barrier heights. Insofar the different field dependences of both models do
not enter the occupancies of the states and thus do not impact the model
behavior.
in the eNMP model occur fast so that the occupancies of the
involved states reach their equilibrium values, which are unaffected by the
barrier heights. Insofar the different field dependences of both models do
not enter the occupancies of the states and thus do not impact the model
behavior.
Besides the ‘anomalous’ defects, the eNMP model also gives an explanation for
‘normal’ defects. They are characterized by the fact that the alternative pathway
from the state 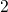 back to
back to 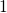 is taken over the metastable state
is taken over the metastable state 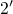 . Thus the hole
emission process is determined by the thermal transition
. Thus the hole
emission process is determined by the thermal transition 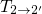 resulting in field
independent emission times as required for this kind of defects. But note
that the TSM has no analog for the ‘normal’ defect behavior and thus must
be viewed as an insufficient description of charge trapping in NBTI and
TDDS.
resulting in field
independent emission times as required for this kind of defects. But note
that the TSM has no analog for the ‘normal’ defect behavior and thus must
be viewed as an insufficient description of charge trapping in NBTI and
TDDS.
In summary, it has been pointed that the physical picture behind of hole trapping in
NBTI is the same for the TSM as well as for the eNMP model. Nevertheless, the
eNMP model should be regarded as an improvement for the two reasons: First, it is
extended by the metastable state 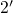 , which allows for the curvature in
, which allows for the curvature in 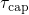 and the
field independence of
and the
field independence of 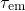 . Second, the NMP formalism is expected to be a better
description of the investigated charge transfer reactions than its simplified MPE
variant used in the TSM. In contrast to the TSM, the eNMP model has
been rigorously derived from one configuration coordinate diagram, which
is regarded as the most complete description of a defect with respect to
energy.
. Second, the NMP formalism is expected to be a better
description of the investigated charge transfer reactions than its simplified MPE
variant used in the TSM. In contrast to the TSM, the eNMP model has
been rigorously derived from one configuration coordinate diagram, which
is regarded as the most complete description of a defect with respect to
energy.
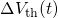 curves and the steps of single events cannot be resolved anymore.
The distribution of hole capture times determines the form of the stress
curves while the corresponding emission times yields the recovery curves.
Consequently, the field acceleration and temperature activation of the time
constants may explain the field and temperature dependences of the NBTI
degradation curves. But one should keep in mind that the permanent component
of NBTI is not captured by TDDS and thus have not been accounted for
in the eNMP model. As a result, a significant contribution to the overall
NBTI degradation is not described by the hole capture and emission process.
curves and the steps of single events cannot be resolved anymore.
The distribution of hole capture times determines the form of the stress
curves while the corresponding emission times yields the recovery curves.
Consequently, the field acceleration and temperature activation of the time
constants may explain the field and temperature dependences of the NBTI
degradation curves. But one should keep in mind that the permanent component
of NBTI is not captured by TDDS and thus have not been accounted for
in the eNMP model. As a result, a significant contribution to the overall
NBTI degradation is not described by the hole capture and emission process.
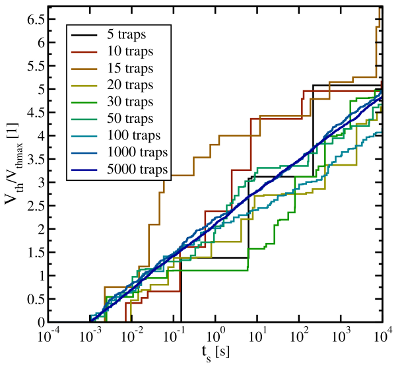
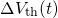 . The barriers for hole capture
are assumed to be homogeneously distributed, resulting in a logarithmic time
behavior. The step height due to one hole capture follow approximately an
exponential dependence in agreement with
. The barriers for hole capture
are assumed to be homogeneously distributed, resulting in a logarithmic time
behavior. The step height due to one hole capture follow approximately an
exponential dependence in agreement with  , which is involved in the hole
capture process, the eNMP model can reproduce the time constants seen
in TDDS. By contrast, a field enhancement factor in the TSM had to be
phenomenologically introduced in order to capture the field dependence
observed in the experimental data. For the aforementioned reasons, the eNMP
model is viewed as an improvement in the description of the hole capture
process.
, which is involved in the hole
capture process, the eNMP model can reproduce the time constants seen
in TDDS. By contrast, a field enhancement factor in the TSM had to be
phenomenologically introduced in order to capture the field dependence
observed in the experimental data. For the aforementioned reasons, the eNMP
model is viewed as an improvement in the description of the hole capture
process.
 in both
models), the defect features a trap level located far below the substrate valence band.
Note that this level is referred to as
in both
models), the defect features a trap level located far below the substrate valence band.
Note that this level is referred to as  in the TSM or
in the TSM or 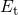 in the eNMP model. If
in the eNMP model. If
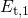 /
/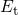 is shifted upwards by the oxide field, the defect can capture a substrate
hole. This is accompanied by a structural relaxation of the defect configuration and
leads to a new trap level
is shifted upwards by the oxide field, the defect can capture a substrate
hole. This is accompanied by a structural relaxation of the defect configuration and
leads to a new trap level 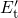 located within or at least close to the substrate
bandgap.
located within or at least close to the substrate
bandgap.
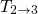 in the TSM or
in the TSM or 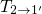 in the eNMP. As mentioned before, the corresponding
trap level is
in the eNMP. As mentioned before, the corresponding
trap level is 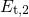 in the TSM and
in the TSM and 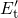 in the eNMP model and lies within or close
to the substrate bandgap. As a result, the occupation of
in the eNMP model and lies within or close
to the substrate bandgap. As a result, the occupation of 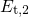 or
or 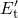 is
strongly dependent of small variations of the substrate Fermi level, also known
as the ‘switching trap’ behavior of defects. Only from the neutral charge
state (the state
is
strongly dependent of small variations of the substrate Fermi level, also known
as the ‘switching trap’ behavior of defects. Only from the neutral charge
state (the state 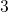 in the TSM and the state
in the TSM and the state 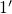 in the eNMP model), the
defect is allowed to return to its initial state
in the eNMP model), the
defect is allowed to return to its initial state 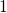 by structural relaxation. In
the state diagrams, the last step corresponds to the transition
by structural relaxation. In
the state diagrams, the last step corresponds to the transition 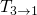 in
the TSM or
in
the TSM or 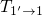 in the eNMP model. It is important to note here that
the hole emission times in both models are eventually controlled by the
position of
in the eNMP model. It is important to note here that
the hole emission times in both models are eventually controlled by the
position of 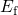 relative to
relative to 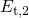 or
or 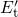 . This effect is reflected in the field
dependence of the ‘anomalous’ defects, on the one hand, and NBTI recovery,
on the other hand. Consider that the transition
. This effect is reflected in the field
dependence of the ‘anomalous’ defects, on the one hand, and NBTI recovery,
on the other hand. Consider that the transition 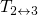 in the TSM and
in the TSM and
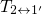 in the eNMP model are actually based on a different description of the
hole capture and emission process. However, the corresponding transition
barriers are assumed to be small in both models. Therefore,
in the eNMP model are actually based on a different description of the
hole capture and emission process. However, the corresponding transition
barriers are assumed to be small in both models. Therefore, 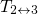 in the TSM
and
in the TSM
and 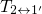 in the eNMP model occur fast so that the occupancies of the
involved states reach their equilibrium values, which are unaffected by the
barrier heights. Insofar the different field dependences of both models do
not enter the occupancies of the states and thus do not impact the model
behavior.
in the eNMP model occur fast so that the occupancies of the
involved states reach their equilibrium values, which are unaffected by the
barrier heights. Insofar the different field dependences of both models do
not enter the occupancies of the states and thus do not impact the model
behavior.
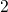 back to
back to 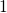 is taken over the metastable state
is taken over the metastable state 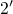 . Thus the hole
emission process is determined by the thermal transition
. Thus the hole
emission process is determined by the thermal transition 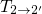 resulting in field
independent emission times as required for this kind of defects. But note
that the TSM has no analog for the ‘normal’ defect behavior and thus must
be viewed as an insufficient description of charge trapping in NBTI and
TDDS.
resulting in field
independent emission times as required for this kind of defects. But note
that the TSM has no analog for the ‘normal’ defect behavior and thus must
be viewed as an insufficient description of charge trapping in NBTI and
TDDS.
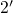 , which allows for the curvature in
, which allows for the curvature in 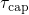 and the
field independence of
and the
field independence of 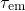 . Second, the NMP formalism is expected to be a better
description of the investigated charge transfer reactions than its simplified MPE
variant used in the TSM. In contrast to the TSM, the eNMP model has
been rigorously derived from one configuration coordinate diagram, which
is regarded as the most complete description of a defect with respect to
energy.
. Second, the NMP formalism is expected to be a better
description of the investigated charge transfer reactions than its simplified MPE
variant used in the TSM. In contrast to the TSM, the eNMP model has
been rigorously derived from one configuration coordinate diagram, which
is regarded as the most complete description of a defect with respect to
energy.