Chapter 7
The Extended Nonradiative Multi-Phonon Model
The Kirton model and the TSM rely on the concept of NMP processes and can
therefore give an explanation for the experimentally observed temperature activation
of 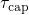 and
and 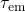 . However, the energy barriers used in those models are not
calculated by the crossing point of two adiabatic potentials, as it would
be necessary according to theoretical considerations. Palma et al. [125]
related the measured capture and emission time constants of RTN to the
properties of oxide defects based on NMP theory. The success of their model
was based on the effect of a Coulomb barrier, which was required to obtain
the correct field dependence of
. However, the energy barriers used in those models are not
calculated by the crossing point of two adiabatic potentials, as it would
be necessary according to theoretical considerations. Palma et al. [125]
related the measured capture and emission time constants of RTN to the
properties of oxide defects based on NMP theory. The success of their model
was based on the effect of a Coulomb barrier, which was required to obtain
the correct field dependence of 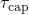 and
and 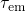 . Irrespective of the physical
correctness of this assumption, the Coulomb barrier was only successfully
applied to MOSFETs with thick dielectrics [184, 125, 123]. In a few RTN
studies [56] as well as in more recent TDDS measurements [53], interesting
phenomena, such as aRTN and tRTN (both discussed in Section 1.3.4), have been
observed. They are linked to quite complex trapping dynamics, which can
only be explained by metastable defect states. Accordingly, a successful,
physics-based NBTI model must incorporate additional metastable defect
configurations in order to account for all experimental results. In a new
modeling attempt, the theoretical framework of NMP charge transfer reactions
has been combined with the concept of metastable states. The resultant
model has been termed extended NMP (eNMP) and will be addressed in the
following.
. Irrespective of the physical
correctness of this assumption, the Coulomb barrier was only successfully
applied to MOSFETs with thick dielectrics [184, 125, 123]. In a few RTN
studies [56] as well as in more recent TDDS measurements [53], interesting
phenomena, such as aRTN and tRTN (both discussed in Section 1.3.4), have been
observed. They are linked to quite complex trapping dynamics, which can
only be explained by metastable defect states. Accordingly, a successful,
physics-based NBTI model must incorporate additional metastable defect
configurations in order to account for all experimental results. In a new
modeling attempt, the theoretical framework of NMP charge transfer reactions
has been combined with the concept of metastable states. The resultant
model has been termed extended NMP (eNMP) and will be addressed in the
following.
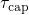 and
and 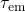 . However, the energy barriers used in those models are not
calculated by the crossing point of two adiabatic potentials, as it would
be necessary according to theoretical considerations. Palma et al. [125]
related the measured capture and emission time constants of RTN to the
properties of oxide defects based on NMP theory. The success of their model
was based on the effect of a Coulomb barrier, which was required to obtain
the correct field dependence of
. However, the energy barriers used in those models are not
calculated by the crossing point of two adiabatic potentials, as it would
be necessary according to theoretical considerations. Palma et al. [125]
related the measured capture and emission time constants of RTN to the
properties of oxide defects based on NMP theory. The success of their model
was based on the effect of a Coulomb barrier, which was required to obtain
the correct field dependence of 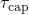 and
and 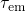 . Irrespective of the physical
correctness of this assumption, the Coulomb barrier was only successfully
applied to MOSFETs with thick dielectrics [184, 125, 123]. In a few RTN
studies [56] as well as in more recent TDDS measurements [53], interesting
phenomena, such as aRTN and tRTN (both discussed in Section 1.3.4), have been
observed. They are linked to quite complex trapping dynamics, which can
only be explained by metastable defect states. Accordingly, a successful,
physics-based NBTI model must incorporate additional metastable defect
configurations in order to account for all experimental results. In a new
modeling attempt, the theoretical framework of NMP charge transfer reactions
has been combined with the concept of metastable states. The resultant
model has been termed extended NMP (eNMP) and will be addressed in the
following.
. Irrespective of the physical
correctness of this assumption, the Coulomb barrier was only successfully
applied to MOSFETs with thick dielectrics [184, 125, 123]. In a few RTN
studies [56] as well as in more recent TDDS measurements [53], interesting
phenomena, such as aRTN and tRTN (both discussed in Section 1.3.4), have been
observed. They are linked to quite complex trapping dynamics, which can
only be explained by metastable defect states. Accordingly, a successful,
physics-based NBTI model must incorporate additional metastable defect
configurations in order to account for all experimental results. In a new
modeling attempt, the theoretical framework of NMP charge transfer reactions
has been combined with the concept of metastable states. The resultant
model has been termed extended NMP (eNMP) and will be addressed in the
following.