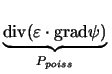 |
= 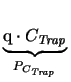 |
(D1) |
![$\displaystyle \underbrace{\rule[-0.3cm]{0cm}{.3cm}\mathrm{div}{\mathbf{J}_{n}}}_{E_{div}}^{}\,$](img613.gif) |
= ![$\displaystyle \underbrace{\rule[-0.3cm]{0cm}{.3cm}\mathrm{q}\cdot\frac{\partial n}{\partial t}}_{E_t}^{}\,$](img615.gif) |
(D2) |
= ![$\displaystyle \underbrace{\rule[-0.3cm]{0cm}{.3cm}-\mathrm{q}\cdot R}_{R}^{}\,$](img617.gif) -
- ![$\displaystyle \underbrace{\rule[-0.3cm]{0cm}{.3cm}\mathrm{q}\cdot\frac{\partial p}{\partial t}}_{H_t}^{}\,$](img618.gif) |
(D3) | |
= q . NC . exp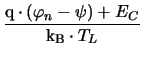
|
(D4) | |
= q . NV . exp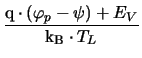
|
(D5) | |
![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}\mathrm{div}\ \mathbf{S}_{n}}_{S_{\mathit{n,div}}}^{}\,$](img621.gif) |
= ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}\mathrm{grad}\left(\frac{E_{C}}{\mathrm{q}} -\psi\right)\cdot\mathbf{J}_{n}}_{S_{\mathit{n,J}}}^{}\,$](img622.gif) -
- ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}\frac{\partial \,(n\cdot T_{n})}{\partial t}}_{S_{\mathit{n,t}}}^{}\,$](img624.gif) +
+ ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}R\cdot T_{n}}_{S_{\mathit{n,R}}}^{}\,$](img625.gif) +
+ ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}n\cdot\frac{T_{n} -T_{L}}{\tau_{\epsilon,n}}}_{S_{\mathit{n,\tau}}}^{}\,$](img626.gif)
|
(D6) |
![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}\mathrm{div}\ \mathbf{S}_{p}}_{S_{\mathit{p,div}}}^{}\,$](img628.gif) |
= ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}\mathrm{grad}\left(\frac{E_{V}}{\mathrm{q}} -\psi\right)\cdot\mathbf{J}_{p}}_{S_{\mathit{p,J}}}^{}\,$](img629.gif) -
- ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}\frac{\partial \,(p\cdot T_{p})}{\partial t}}_{S_{\mathit{p,t}}}^{}\,$](img631.gif) +
+ ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}R\cdot T_{p}}_{S_{\mathit{p,R}}}^{}\,$](img632.gif) +
+ ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}p\cdot\frac{T_{p} -T_{L}}{\tau_{\epsilon,p}}}_{S_{\mathit{p,\tau}}}^{}\,$](img633.gif)
|
(D7) |
![$\displaystyle \underbrace{\rule[-0.3cm]{0cm}{.3cm}\mathrm{div}\ \mathbf{S}_L}_{T_{\mathit{div}}}^{}\,$](img635.gif) |
= ![$\displaystyle \underbrace{\rule[-0.3cm]{0cm}{.3cm}\rho_{\mathrm{L}}\cdot c_{\mathrm{L}}\cdot\frac{\partial T_{L}}{\partial t}}_{T_t}^{}\,$](img637.gif) |
(D8) |
When used for the first time, for each equation the appropriate quantities are automatically created and initialized with proper initial values. These initial values are either taken from a previous simulation or are calculated to give reasonable defaults as follows.
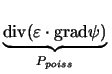 |
= 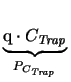 |
(D1) |
![$\displaystyle \underbrace{\rule[-0.3cm]{0cm}{.3cm}\mathrm{div}{\mathbf{J}_{n}}}_{E_{div}}^{}\,$](img613.gif) |
= ![$\displaystyle \underbrace{\rule[-0.3cm]{0cm}{.3cm}\mathrm{q}\cdot\frac{\partial n}{\partial t}}_{E_t}^{}\,$](img615.gif) |
(D2) |
= ![$\displaystyle \underbrace{\rule[-0.3cm]{0cm}{.3cm}-\mathrm{q}\cdot R}_{R}^{}\,$](img617.gif) -
- ![$\displaystyle \underbrace{\rule[-0.3cm]{0cm}{.3cm}\mathrm{q}\cdot\frac{\partial p}{\partial t}}_{H_t}^{}\,$](img618.gif) |
(D3) | |
= q . NC . exp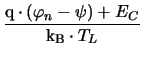
|
(D4) | |
= q . NV . exp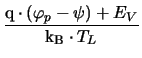
|
(D5) | |
![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}\mathrm{div}\ \mathbf{S}_{n}}_{S_{\mathit{n,div}}}^{}\,$](img621.gif) |
= ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}\mathrm{grad}\left(\frac{E_{C}}{\mathrm{q}} -\psi\right)\cdot\mathbf{J}_{n}}_{S_{\mathit{n,J}}}^{}\,$](img622.gif) -
- ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}\frac{\partial \,(n\cdot T_{n})}{\partial t}}_{S_{\mathit{n,t}}}^{}\,$](img624.gif) +
+ ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}R\cdot T_{n}}_{S_{\mathit{n,R}}}^{}\,$](img625.gif) +
+ ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}n\cdot\frac{T_{n} -T_{L}}{\tau_{\epsilon,n}}}_{S_{\mathit{n,\tau}}}^{}\,$](img626.gif)
|
(D6) |
![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}\mathrm{div}\ \mathbf{S}_{p}}_{S_{\mathit{p,div}}}^{}\,$](img628.gif) |
= ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}\mathrm{grad}\left(\frac{E_{V}}{\mathrm{q}} -\psi\right)\cdot\mathbf{J}_{p}}_{S_{\mathit{p,J}}}^{}\,$](img629.gif) -
- ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}\frac{\partial \,(p\cdot T_{p})}{\partial t}}_{S_{\mathit{p,t}}}^{}\,$](img631.gif) +
+ ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}R\cdot T_{p}}_{S_{\mathit{p,R}}}^{}\,$](img632.gif) +
+ ![$\displaystyle \underbrace{\rule[-0.4cm]{0cm}{.4cm}p\cdot\frac{T_{p} -T_{L}}{\tau_{\epsilon,p}}}_{S_{\mathit{p,\tau}}}^{}\,$](img633.gif)
|
(D7) |
![$\displaystyle \underbrace{\rule[-0.3cm]{0cm}{.3cm}\mathrm{div}\ \mathbf{S}_L}_{T_{\mathit{div}}}^{}\,$](img635.gif) |
= ![$\displaystyle \underbrace{\rule[-0.3cm]{0cm}{.3cm}\rho_{\mathrm{L}}\cdot c_{\mathrm{L}}\cdot\frac{\partial T_{L}}{\partial t}}_{T_t}^{}\,$](img637.gif) |
(D8) |
Currently two different versions of
Ediv exist depending on the
current model used ((3.5) or (3.7)), namely
EdivDD and
EdivHD, vice-versa for
holes. The groups resulting from the equation assembly models given above are
listed in Table D.1.
| Group name | Equation assembly models |
| electrons | EdivDD, Pn |
| electronsTrans | Et |
| electronsQFL | PnQFL |
| electronsHD |
EdivHD, Pn,
Sn, div,
Sn, J,
Sn, |
| electronsHDTrans | Et, Sn, t |
| holes | HdivDD, Ph |
| holesTrans | Ht |
| holesQFL | PpQFL |
| holesHD |
HdivHD, Pp,
Sp, div,
Sp, J,
Sp, |
| holesHDTrans | Ht, Sp, t |
| potential | Ppoiss, PC |
| <recombination> | R,, PCTrap, Sn, R, Sp, R |
| selfHeating | Tdiv, TH |
| selfHeatingTrans | Tt |
Iterate
{
Scheme
{
models = "potential,potentialInt";
...
}
}
If one is also interested in the electron concentration, e.g., in the channel of a HEMT, the electron group has to be added:
Iterate
{
Scheme
{
models = "potential,potentialInt,electrons,electronsInt";
...
}
}
If the derivative of the electron concentration with respect to time is relevant, e.g., for a transient simulation, the electronTrans group has to be added:
Iterate
{
Scheme
{
models = "potential,potentialInt,"
"electrons,electronsInt,electronsTrans";
...
}
}
| Group Name | Created Quantity Classes |
| electrons | Potential |
| ElectronConcentration | |
| electronsTrans | ElectronConcentration |
| electronsQFL | Potential |
| ElectronConcentration | |
| electronsHD | Potential |
| ElectronConcentration | |
| ElectronTemperature | |
| electronsHDTrans | ElectronConcentration |
| holes | Potential |
| HoleConcentration | |
| holesTrans | HoleConcentration |
| holesQFL | Potential |
| HoleConcentration | |
| holesHD | Potential |
| HoleConcentration | |
| HoleTemperature | |
| holesHDTrans | HoleConcentration |
| potential | Potential |
| <recombination> | Potential |
| ElectronConcentration | |
| HoleConcentration | |
| selfHeating | LatticeTemperature |
| selfHeatingTrans | LatticeTemperature |
| potentialInt | Potential on both segments |
| electronsInt | Potential on both segments |
| ElectronConcentration on both segments | |
| electronsHDInt | Potential on both segments |
| ElectronConcentration on both segments | |
| ElectronTemperature on both segments | |
| terminal | ContactVoltage |
| ContactCurrent | |
| ContactCharge | |
| ContactTemperature | |
| BoundaryCurrent | |
| BoundaryElectronCurrent | |
| BoundaryHoleCurrent | |
| BoundaryConductionCurrent | |
| BoundaryDisplacementCurrent |
As pointed out above, each group automatically creates the quantities
which form the unknowns of the equation system. Each quantity belongs
to a so-called quantity class, e.g., the potentials inside all insulator,
conductor, and semiconductor segments belong to the quantity class
Potential. Table D.2 lists the quantity
classes and the model groups which create them. It is important to note that
each quantity is created and initialized when it is first requested by one of
the model groups. The mere creation of a quantity does not imply that there
is a controlling equation available. In case the user registers only the
electrons group on one segment, the quantities ![]() and n are
created. The potential
and n are
created. The potential ![]() is initialized to the built-in potential
whereas the electron concentration n is computed using a charge-neutrality
assumption. As there has been no Poisson equation requested (group
Potential has not been used), the electron continuity equation will
be solved stand-alone.
is initialized to the built-in potential
whereas the electron concentration n is computed using a charge-neutrality
assumption. As there has been no Poisson equation requested (group
Potential has not been used), the electron continuity equation will
be solved stand-alone.
The same is true for interface models. When using for instance the HD interface group, carrier temperature quantities on both sides of the interface are created and are initialized to the lattice temperature. However, by simply creating these quantities the interface model does not make any assumptions about the transport models used on either side. It is possible to use a DD model on one side and a HD model on the other side which implies an equilibrium boundary condition for the carrier temperatures as the carrier temperatures are set equal to the lattice temperature in this case.
The terminal group needs some further attention. It creates an abundance of quantities which might seem unnecessary at a first glance. The quantities whose names start with Contact are the terminal quantities which are used to formulate the boundary conditions. The quantities with names beginning with Boundary are supplementary quantities which represent the current components and are used to simplify calculation of the contact current.
For mixed-mode simulations the basic semiconductor equations are augmented by the circuit equations resulting from the modified nodal approach (MNA) and the MNA equations for the thermal equivalent circuit. It is worthwhile to note that for the KCL equation the node voltage vector is split into two quantity classes namely node voltages (NodeVoltage) and fixed node voltages (FixNodeVoltage), respectively. Since each quantity class can be marked separately for the solving process, this separation has the major advantage that the fixed node voltage class can be arbitrarily solved or not. One way to utilize this feature is to emulate the behavior of typical circuit simulators like SPICE. To aid convergence, SPICE allows the user to set some critical node voltages to a constant value, iterate until convergence, release the critical node voltages, and continue iteration until final convergence. This has been implemented in the MixedDD and MixedHD iteration schemes.
Schemes
{
MixedDD
{
DDPre : DDBlock
{
ignoreQuantities = "FixNodeVoltage";
}
DDPre : DDBlock;
}
}
Iterate
{
Scheme : ~Schemes.MixedDD;
}
However, due to the generality of this concept, it is possible to design own iteration schemes with a different behavior. One useful possibility might be to fix some node voltages only at distinct time points to their initial or last value (which is internally the same).