2.3.4 Generation/Recombination Processes
In indirect gap semiconductors, such as silicon and germanium, it was found experimentally
that generation/recombination occurs primarily via trap centers. A theory of this effect has
been established by SHOCKLEY and READ [41] and HALL
[42].
Figure 2.5:
Symbolic band diagram showing the four partial processes involved in indirect
generation/recombination.
|
![\includegraphics[width=.315\textwidth]{eps/GenRecBand.eps}](img628.png) |
Interaction among the partial systems electrons, holes, and traps is described by four partial
processes (Fig. 2.5)
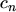 :
:- Electron capture. An electron from the conduction band is trapped by an
unoccupied defect which becomes occupied.
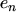 :
:- Electron emission. An electron from an occupied trap moves to the conduction
band. The trap becomes unoccupied.
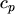 :
:- Hole capture. An electron from an occupied trap moves to the valence band and
neutralizes a hole. The trap becomes unoccupied.
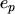 :
:- Hole emission. An electron from the valence band is trapped by a defect, thus
leaving a hole in the valence band and an occupied trap.
Here 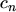 ,
, 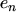 ,
, 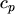 ,
, 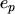 are the respective rate constants. This description assumes
acceptor-like traps which can exist in a neutral or a negatively charged state. Donor-like
traps, which have a neutral and a positively charged state, lead however to exactly the same
expression for the net recombination rate.
are the respective rate constants. This description assumes
acceptor-like traps which can exist in a neutral or a negatively charged state. Donor-like
traps, which have a neutral and a positively charged state, lead however to exactly the same
expression for the net recombination rate.
The generation- and recombination rates of electrons/holes within an energy interval
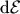 are described by the law of mass action which states that the rates
are proportional to the concentration of the involved reactants [43, p.54]
are described by the law of mass action which states that the rates
are proportional to the concentration of the involved reactants [43, p.54]
The occupation probability of an energy level is given by the FERMI-DIRAC
statistics
with  ,
, 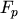 , and
, and  being the respective quasi FERMI levels and
being the respective quasi FERMI levels and 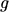 the
ground-state degeneracy of the trap [44, p.122] which is assumed to be 1 in
the following.
the
ground-state degeneracy of the trap [44, p.122] which is assumed to be 1 in
the following.
Subsections
M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF
![\includegraphics[width=.315\textwidth]{eps/GenRecBand.eps}](img628.png)
![]() are described by the law of mass action which states that the rates
are proportional to the concentration of the involved reactants [43, p.54]
are described by the law of mass action which states that the rates
are proportional to the concentration of the involved reactants [43, p.54]