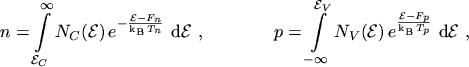The trap occupation probability  can be calculated by examining the steady state
in which the following relation holds2.12
can be calculated by examining the steady state
in which the following relation holds2.12
 |
(2.211) |
For the non degenerated case, that is, for the FERMI level several
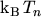 below
below
 ,
,
 , MAXWELL-BOLTZMANN
statistics can be assumed
, MAXWELL-BOLTZMANN
statistics can be assumed
 |
(2.212) |
which further allows to assume
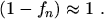 |
(2.213) |
Using the approximations (2.212) and (2.213)
and the analog approximations for holes, equations (2.209) and
(2.210) can be written as
where 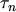 and
and  are the lifetimes for electrons and holes, respectively. The
characteristic parameters describing the interaction of carriers and trap centers are the
capture cross sections
are the lifetimes for electrons and holes, respectively. The
characteristic parameters describing the interaction of carriers and trap centers are the
capture cross sections 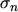 and
and 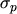 . If they are known the rate constants (and
thus also the lifetimes) can be expressed as
. If they are known the rate constants (and
thus also the lifetimes) can be expressed as
 |
(2.216) |
where
 and
and
 are the thermal velocities of electrons and
holes, respectively.
are the thermal velocities of electrons and
holes, respectively.
Using the following expressions for the electron and hole concentrations
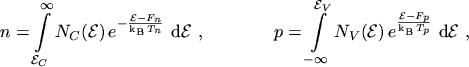 |
(2.217) |
and the handy abbreviations 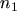 and
and  for the electron and hole concentrations when the
FERMI level is equal to the trap level
for the electron and hole concentrations when the
FERMI level is equal to the trap level
eqns. (2.214) and (2.215) can be written as
Making use of the steady state condition eqn. (2.211) the following
expression for  is found
is found
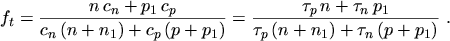 |
(2.222) |
Inserting eqn. (2.222) either in eqn. (2.214) or eqn. (2.215) yields
the well known SHOCKLEY-READ-HALL net recombination rate
 |
(2.223) |
M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF