2.3.4.3 Higher Order Moments

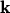Integration of eqns. (2.209) and (2.210) led to the generation/recombination term which contributes to the carrier continuity equation. The contributions to the higher order moment equations are obtained by calculating the moments of the net recombination term in $\ensuremath{\boldsymbol{\mathrm{k}}}$ -space

$\displaystyle \mathcal{R}$	$\displaystyle = \frac{1}{\tau_n} \, \Bigl( (1 - f_t) \, f_n - f_t \, e^{- \frac{\mathcal{E}- \mathcal{E}_t}{\mathrm{k}_\mathrm{B}\, T_\mathrm{L}}} \Bigr) \ ,$	(2.224)
$\displaystyle \ensuremath{\int \ensuremath{\widetilde{\phi}}_j \, \mathcal{R} \,\, \ensuremath{\mathrm{d}}^3 k}$	$\displaystyle = \frac{1}{\tau_n} \, \Bigl( (1 - f_t) \, \ensuremath{\langle \en... ..._t \, \ensuremath{\langle \ensuremath{\widetilde{\phi}}_j \rangle}_1 \Bigr) \ ,$	(2.225)

with

$\displaystyle \ensuremath{\langle \ensuremath{\widetilde{\phi}}_j \rangle}= \en... ...t} {\mathrm{k}_\mathrm{B}\, T_\mathrm{L}}} \,\, \ensuremath{\mathrm{d}}^3 k}\ ,$

(2.226)

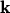where an energy independent carrier lifetime has been assumed and the approximation (2.213) has been used. Since the subsequent integration is carried out in $\ensuremath{\boldsymbol{\mathrm{k}}}$ -space rather than in the energy domain, the effective density of states does not appear ( $N_C \, \mathrm{d}\mathcal{E}\equiv \mathrm{d}^3 k$ ) due to the normalization of the distribution function, $\ensuremath{\langle 1 \rangle} = n$ .

Using eqns. (2.93) to (2.95) together with eqn. (2.225) yields

$\displaystyle \phi_0$	$\displaystyle :$	$\displaystyle \textcolor{lightgrey}{.......}R$	$\displaystyle =$	$\displaystyle \frac{1}{\tau_n} \,$	$\displaystyle \Bigl( (1 - f_t) \, n$	$\displaystyle - f_t \, n_1 \Bigr) \ ,$	(2.227)
$\displaystyle \phi_2$	$\displaystyle :$	$\displaystyle \textcolor{lightgrey}{.......}G_{\mathcal{E}\, n}$	$\displaystyle =$	$\displaystyle \frac{3}{2} \, \frac{\mathrm{k}_\mathrm{B}}{\tau_n} \,$	$\displaystyle \Bigl( f_t \, n_1 \, T_\mathrm{L}$	$\displaystyle - (1 - f_t) \, n \, T_n \Bigr) \ ,$	(2.228)
$\displaystyle \phi_4$	$\displaystyle :$	$\displaystyle \textcolor{lightgrey}{.......}G_{\beta \, n}$	$\displaystyle =$	$\displaystyle \frac{5 \cdot 3}{2} \, \frac{\mathrm{k}_\mathrm{B}^2} {m \, \tau_n} \,$	$\displaystyle \Bigl( f_t \, n_1 \, T_\mathrm{L}^2$	$\displaystyle - (1 - f_t) \, n \, T_n^2 \, \beta_n \Bigr) \ .$	(2.229)

Eqn. (2.228) is written as a net power generation rate

$\displaystyle G_{\mathcal{E}\, n} = - \ensuremath{\int \mathcal{E}\, \mathcal{R}(k) \,\, \ensuremath{\mathrm{d}}^3 k}\ .$

(2.230)

The index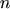

must be used since in contrast to the net recombination rate the net energy generation rate is different for both carrier types.

The contribution to the moment equations of odd order can be neglected since the right hand sides of eqns. (2.76) to (2.78) are several orders of magnitude larger than the additional generation term^2.13.

Rewriting eqn. (2.228) leads to

$\displaystyle G_{\mathcal{E}\, n}$	$\displaystyle = - \frac{3}{2} \, \frac{\mathrm{k}_\mathrm{B}}{\tau_n} \, \Bigl(... ..._t \bigl( n \, T_n + n_1 \, T_\mathrm{L}+ n_1 \, T_n - n_1 \, T_n \bigr) \Bigr)$	(2.231)
	$\displaystyle = - \frac{3}{2} \, \mathrm{k}_\mathrm{B}\, \Bigl( T_n \, \underbr... ...{\frac{f_t \, n_1}{\tau_n}}_{\textstyle G_n} \, (T_n - T_\mathrm{L}) \Bigr) \ .$	(2.232)

Eqn. (2.229) can be manipulated in the same way, so the even moments read

$\displaystyle \phi_0$	$\displaystyle :$	$\displaystyle \textcolor{lightgrey}{.......}R$	$\displaystyle = \frac{n \, p - n_i^2} {\tau_p \, (n + n_1) + \tau_n \, (p + p_1)} \ ,$	(2.233)
$\displaystyle \phi_2$	$\displaystyle :$	$\displaystyle \textcolor{lightgrey}{.......}G_{\mathcal{E}\, n}$	$\displaystyle = - \frac{3}{2} \, \mathrm{k}_\mathrm{B}\, \Bigl( \bigl( R_n - G_n \bigr) \, T_n + G_n \, \bigl( T_n - T_\mathrm{L}\bigr) \Bigr) \ ,$	(2.234)
$\displaystyle \phi_4$	$\displaystyle :$	$\displaystyle \textcolor{lightgrey}{.......}G_{\beta \, n}$	$\displaystyle = - \frac{5 \cdot 3}{2} \, \frac{\mathrm{k}_\mathrm{B}^2}{m} \, \... ... \, \beta_n + G_n \, \bigl( T_n^2 \, \beta_n - T_\mathrm{L}^2 \bigr) \Bigr) \ .$	(2.235)

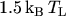The interpretation of eqn. (2.234) is that a recombining electron on average removes the energy $1.5 \, \mathrm{k}_\mathrm{B}\, T_n$ from the system, while a generated electron introduces an energy of only $1.5 \, \mathrm{k}_\mathrm{B}\, T_\mathrm{L}$ , which means that generated electrons are initially cold.

M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF


Previous: 2.3.4.2 Steady State Up: 2.3.4 Generation/Recombination Processes Next: 3. Discretization