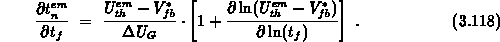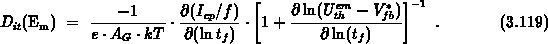3.3.2 Emission in the Non-Steady-State Mode




Next: 3.4 Geometric Current Component
Up: 3.3 Analytical Modeling of
Previous: Frequency-Dependence of the
In the preceeding section a model of the charge-pumping current is presented
for the large-signal trapezoidal gate pulses. A step approximation of the
non-steady-state occupancy function is assumed in the derivation. In the
engineering applications of charge pumping the most important quantity is
the maximal charge-pumping current at the upper plateau of the 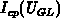 curve. In this region, the active energy interval contributing to the
current is determined by the non-steady-state emission levels of electrons
curve. In this region, the active energy interval contributing to the
current is determined by the non-steady-state emission levels of electrons
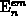 and holes
and holes 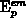 . In order to evaluate the error
introduced by a step approximation of the occupancy function we will discuss
the three-level gate waveform shown in Figure 3.3, instead of
the trapezoidal waveform. In the three-level technique the electron emission
time is exactly known and equals to the mid-level duration
. In order to evaluate the error
introduced by a step approximation of the occupancy function we will discuss
the three-level gate waveform shown in Figure 3.3, instead of
the trapezoidal waveform. In the three-level technique the electron emission
time is exactly known and equals to the mid-level duration 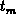 if the falling
edges are sufficiently abrupt (
if the falling
edges are sufficiently abrupt (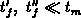 ). By considering the
three-level method, an eventual error in the determination of the emission time
). By considering the
three-level method, an eventual error in the determination of the emission time
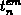 , which can result from an inaccurate
, which can result from an inaccurate 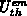 and
and 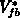 ,
is avoided. In the three-level method, it is assumed that all available traps
are filled by electrons at the top level and recombined by holes at the bottom
level. When the falling edges are abrupt the
,
is avoided. In the three-level method, it is assumed that all available traps
are filled by electrons at the top level and recombined by holes at the bottom
level. When the falling edges are abrupt the 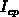 is given by
is given by
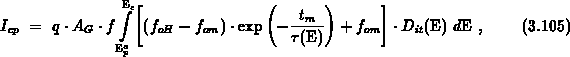
where 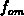 is the steady-state occupancy function at the mid level
is the steady-state occupancy function at the mid level
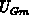 and
and 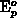 is the lower energy boundary
(
is the lower energy boundary
(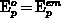 in the conditions of interest here).
We further assume
in the conditions of interest here).
We further assume 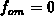 for traps of interest and a level
for traps of interest and a level 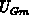 high sufficiently that the hole capture is negligible during
high sufficiently that the hole capture is negligible during 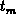 .
Consequently,
.
Consequently, 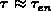 .
.
For not too short 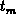 the steady-state occupancy function
the steady-state occupancy function 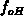 may also
be approximated by a step-like function at
may also
be approximated by a step-like function at 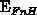 and
and 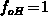 holds for traps of interest.
holds for traps of interest.
By introducing a level 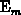 so that
so that
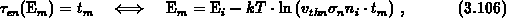
expression 3.105 reduces to
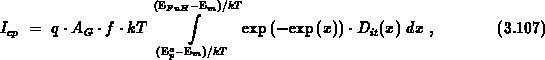
where 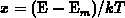 . The subintegral function
. The subintegral function
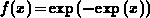 is the solution for the occupancy function
in the non-steady-state emission mode when
is the solution for the occupancy function
in the non-steady-state emission mode when
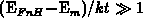 . A general solution, also valid for
short time intervals
. A general solution, also valid for
short time intervals 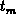 is shown in 3.105. The
function
is shown in 3.105. The
function 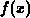 is independent of
is independent of 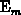 , namely of the observation time
, namely of the observation time
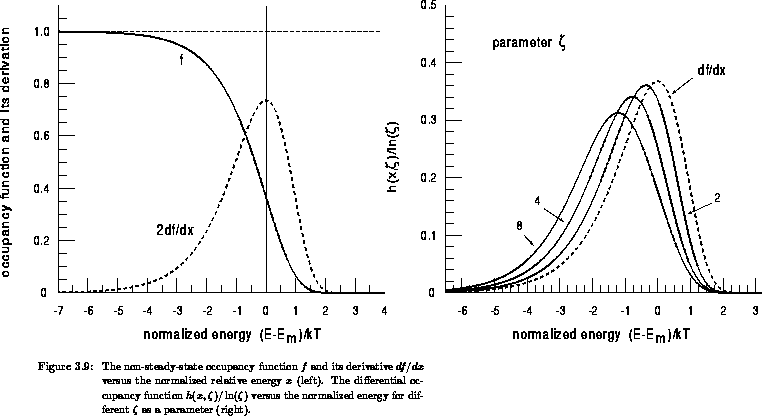
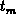 . It is plotted by the solid line in
Figure 3.9 (left). This function is not
symmetrical with respect to
. It is plotted by the solid line in
Figure 3.9 (left). This function is not
symmetrical with respect to 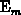 . The width of the transition region
from an occupancy of
. The width of the transition region
from an occupancy of 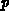 to an occupancy of
to an occupancy of 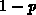 is given by
is given by
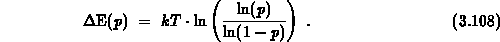
For example, the interval from 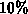 to
to 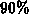 trap occupancy has a width
of
trap occupancy has a width
of 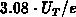 , which is not negligible with respect to the band gap.
, which is not negligible with respect to the band gap.
On the other hand, in a step approximation of the non-steady-state occupancy
function one may write
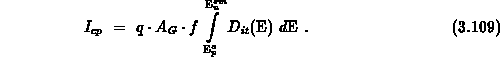
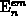 is the emission level we are looking for. In common cases, it
may be assumed that
is the emission level we are looking for. In common cases, it
may be assumed that 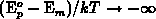 and
and
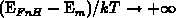 . The emission level
. The emission level
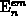 can be derived by equaling
can be derived by equaling 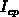 given by
expressions 3.105 and 3.109.
given by
expressions 3.105 and 3.109.
In a standard approximation 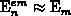 , where
, where
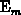 is defined by 3.106 [206][154].
Note that a general expression for
is defined by 3.106 [206][154].
Note that a general expression for 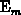 valid also for
valid also for 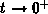 has
been discussed in [435][232]. However, observing the non-steady-state
occupancy function shown in Figure 3.9 (left) we
conclude that many traps below the level
has
been discussed in [435][232]. However, observing the non-steady-state
occupancy function shown in Figure 3.9 (left) we
conclude that many traps below the level 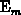 have emitted during
have emitted during 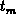 ,
while the traps above
,
while the traps above 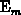 are emptied almost in complete. Therefore,
are emptied almost in complete. Therefore,
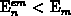 . It follows the equation with respect to
. It follows the equation with respect to
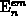
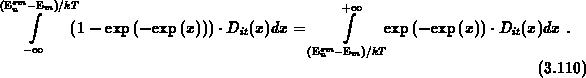
Let us assume a constant 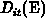 . A substitution of
. A substitution of
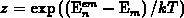 in 3.110 yields the equation
in 3.110 yields the equation
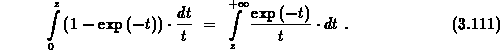
The right-hand-side in 3.111 is the 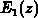 function,
whereas the left-hand-side is the
function,
whereas the left-hand-side is the 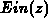 function ([3]). Taking
advantage of the relationship
function ([3]). Taking
advantage of the relationship 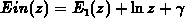 , where
, where
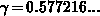 is the Euler constant, one obtains
is the Euler constant, one obtains
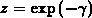 for the solution of 3.111.
Finally,
for the solution of 3.111.
Finally,
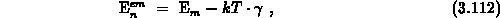
where 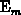 is defined by 3.106. For the hole
emission level the correction becomes
is defined by 3.106. For the hole
emission level the correction becomes 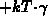 . The
. The 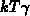 shift is small, but not negligible in comparison with the active energy
interval which is less than
shift is small, but not negligible in comparison with the active energy
interval which is less than 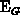 . When accounting for both, the
electron and the hole non-steady-state emission the reduction of the active
energy interval becomes
. When accounting for both, the
electron and the hole non-steady-state emission the reduction of the active
energy interval becomes 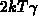 , which is
, which is 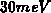 at room temperature.
This can result in
at room temperature.
This can result in 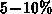 reduction in
reduction in 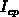 .
.
For real Si-SiO interfaces
interfaces 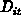 can significantly vary with energy
along the forbidden band, particularly close to the band edges. To estimate
the correction of
can significantly vary with energy
along the forbidden band, particularly close to the band edges. To estimate
the correction of 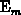 in these cases we assume an exponential
test distribution of
in these cases we assume an exponential
test distribution of 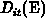 . A simple replacement in
equation 3.110 leads to
. A simple replacement in
equation 3.110 leads to
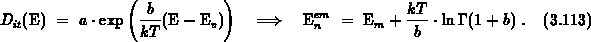
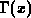 is the Gamma function. The factor
is the Gamma function. The factor
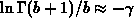 for small
for small 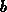 , which is a typical case
in practice. For example, assuming a variation of the trap density in the
upper half of the band gap so that
, which is a typical case
in practice. For example, assuming a variation of the trap density in the
upper half of the band gap so that
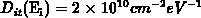 at the mid-gap and
at the mid-gap and
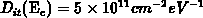 at the band edge, it
follows
at the band edge, it
follows 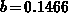 and
and 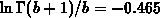 . Therefore, an
exponentially varying
. Therefore, an
exponentially varying 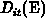 function also can be nearly considered
as a slowly varying within the interval around
function also can be nearly considered
as a slowly varying within the interval around 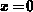 where the occupancy
function
where the occupancy
function 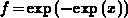 changes rapidly. As a conclusion, the
correction
changes rapidly. As a conclusion, the
correction 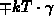 is a valid approximation in all cases of
practical interest.
is a valid approximation in all cases of
practical interest.
In the previous section we have obtained that the analytical model
overestimates the maximal 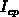 in Figures 3.6. When the
in Figures 3.6. When the
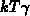 shift is taken into account for both,
shift is taken into account for both, 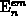 and
and
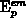 levels the maximal current agrees well with the numerical
calculation, as is shown for the same example in Figure 3.7.
levels the maximal current agrees well with the numerical
calculation, as is shown for the same example in Figure 3.7.
In order to analyze the accuracy of the analytical model on large time scales,
we calculate the charge recombined per one period 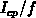 over
over 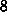 decades of
the fall and rise times. The calculated family of the curves is shown in
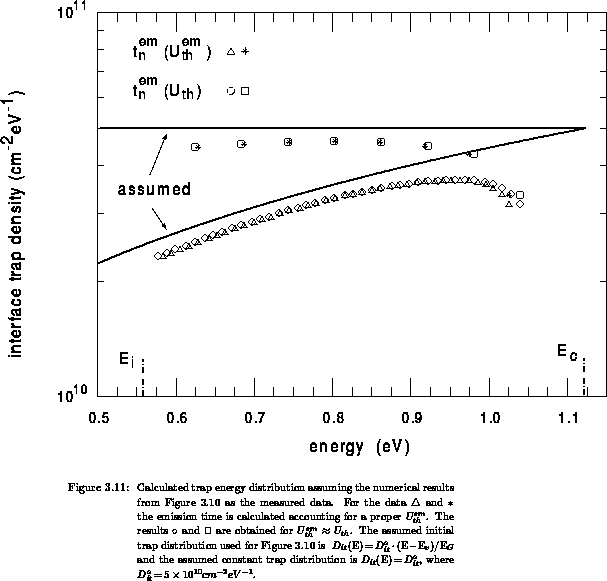
Figure 3.10, together with the rigorous numerical
result. The assumed trap density is linearly distributed across the band gap
decades of
the fall and rise times. The calculated family of the curves is shown in
Figure 3.10, together with the rigorous numerical
result. The assumed trap density is linearly distributed across the band gap
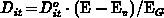 and is shown in
Figure 3.11. The gate signal switches the interface
from strong inversion at
and is shown in
Figure 3.11. The gate signal switches the interface
from strong inversion at 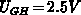 to strong accumulation at
to strong accumulation at
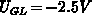 . In this case,
. In this case, 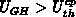 and
and
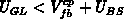 are fulfilled for all
are fulfilled for all 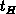 and
and 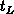 , including
the shortest considered (see Figure 3.8 for a similar
device). Therefore, the
, including
the shortest considered (see Figure 3.8 for a similar
device). Therefore, the 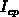 is solely determined by the non-steady-state
emission levels of electrons and holes. In the numerical calculations the
traps only reside in the channel where the spatial conditions are uniform. For
the numerical results we assume the DC component of the net generation rates
is solely determined by the non-steady-state
emission levels of electrons and holes. In the numerical calculations the
traps only reside in the channel where the spatial conditions are uniform. For
the numerical results we assume the DC component of the net generation rates
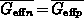 , because of a very
large geometric component occurring in
, because of a very
large geometric component occurring in 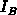 for
for 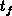 in the
in the 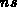 -range. Note
that the frequency applied in the calculations is unacceptably high for
-range. Note
that the frequency applied in the calculations is unacceptably high for
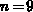 and low for
and low for 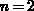 and
and 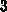 , regarding practical measurements.
In all analytical calculations we adopt
, regarding practical measurements.
In all analytical calculations we adopt 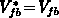 and
and
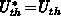 .
.
When assuming a most simple approximation 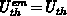 and
and
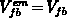 the analytical model remarkably overestimates
the analytical model remarkably overestimates 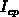 at short
at short 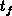 and
and 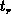 in the
in the 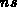 -range and underestimates
-range and underestimates 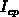 at long
at long
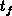 and
and 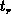 in the
in the  -range (these results are not shown here). In a
better approach
-range (these results are not shown here). In a
better approach 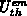 and
and 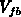 are calculated for a specified
are calculated for a specified 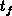 and
and 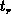 , as is explained in the preceding section. The resulting
, as is explained in the preceding section. The resulting 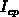 is
shown by the solid lines in Figure 3.10. We still
overestimate
is
shown by the solid lines in Figure 3.10. We still
overestimate 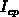 in the
in the  -range, but less than for
-range, but less than for
 . At very
. At very
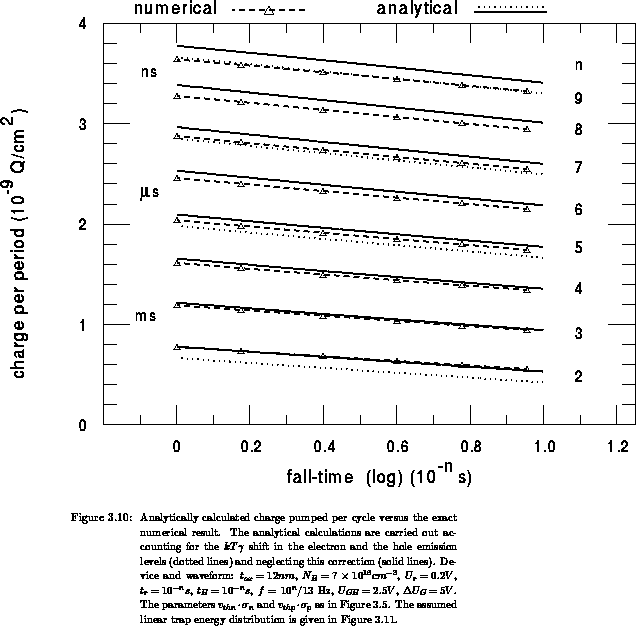
short fall times  holds, which results in a longer
holds, which results in a longer
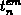 and a lower
and a lower 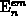 when accounting for a proper
when accounting for a proper
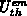 . If the correction
. If the correction 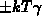 is taken into account the
agreement with the numerical result is excellent in the sub-
is taken into account the
agreement with the numerical result is excellent in the sub-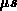 range
(dotted curves which are shown for some time decades). However, the
range
(dotted curves which are shown for some time decades). However, the 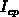 is too low at long
is too low at long 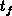 and
and 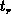 in the later case.
in the later case.
We attribute the later finding to the variation in the capture-onset levels
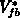 and
and 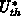 with
with 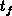 and
and 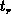 , respectively. This explanation
is fully supported by the numerical simulations. By observing the evolution of
the terminal currents and the total electron and hole interface net generation
rates,
, respectively. This explanation
is fully supported by the numerical simulations. By observing the evolution of
the terminal currents and the total electron and hole interface net generation
rates, 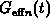 and
and 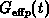 , during the fall edge of
the gate pulse we found that
, during the fall edge of
the gate pulse we found that 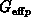 becomes dominant over
becomes dominant over
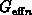 at
at 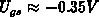 for
for 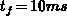 and at
and at
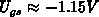 for
for 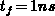 . However, while in the case for
. However, while in the case for
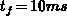 the hole capture stops rapidly the electron emission, in the
case for
the hole capture stops rapidly the electron emission, in the
case for 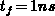 the traps also continue to emit in the condition
the traps also continue to emit in the condition
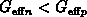 until the level
until the level 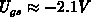 is
exceeded. Moreover, the study of the geometric component presented in
Section 3.4 shows that the electrons emitted in the conduction band
when a significant hole capture occurs are mostly not collected by the source
and drain junctions, but are injected into the bulk, thereby building an
additional geometric component in the measured charge-pumping current. The
analytically calculated emission-onset voltages are
is
exceeded. Moreover, the study of the geometric component presented in
Section 3.4 shows that the electrons emitted in the conduction band
when a significant hole capture occurs are mostly not collected by the source
and drain junctions, but are injected into the bulk, thereby building an
additional geometric component in the measured charge-pumping current. The
analytically calculated emission-onset voltages are 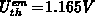 and
and 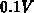 for
for 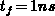 and
and 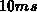 , respectively. The device voltages are
, respectively. The device voltages are
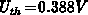 and
and 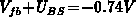 . Consequently, the
variation of
. Consequently, the
variation of 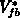 with
with 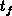 is of the same order as the variation of
is of the same order as the variation of
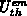 with
with 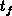 . Only the later effect is included in our present
analytical model. It is worth to point out that the former effect was never
considered, modeled nor included in the charge-pumping theory. The same
conclusions hold when considering the level
. Only the later effect is included in our present
analytical model. It is worth to point out that the former effect was never
considered, modeled nor included in the charge-pumping theory. The same
conclusions hold when considering the level 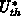 as a function of
as a function of 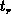 .
Note that increasing
.
Note that increasing 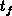 leads to an increase in
leads to an increase in 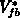 , shortening of
, shortening of
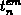 and consequently,
and consequently, 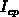 increases.
increases.
We propose that the changes in 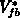 with
with 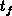 can be analytically
calculated by adopting the assumption
can be analytically
calculated by adopting the assumption
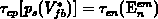 . It is a trivial task
to reduce the problem to a coupled system of two implicit algebraic equations,
which can be simply solved. These results will be presented in a further study.
. It is a trivial task
to reduce the problem to a coupled system of two implicit algebraic equations,
which can be simply solved. These results will be presented in a further study.
Finally, it is concluded that for the trapezoidal waveform an exact
determination of the non-steady-state emission time for electrons and holes is
not possible without significant increasing of model complexity.
In the following, the extraction of the energy distribution of trap density
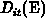 from the experimental
from the experimental 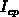 characteristics is studied.
We employ the numerically calculated data shown in
Figure 3.10 instead of the experimental data. This
characteristic is obtained assuming a linear trap distribution shown by the
solid line in Figure 3.11. The deviation of the
extracted
characteristics is studied.
We employ the numerically calculated data shown in
Figure 3.10 instead of the experimental data. This
characteristic is obtained assuming a linear trap distribution shown by the
solid line in Figure 3.11. The deviation of the
extracted 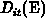 from the assumed one serves as a direct monitor for
the accuracy of the extraction methods.
from the assumed one serves as a direct monitor for
the accuracy of the extraction methods.
When the 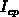 is controlled by the electron emission level the
differentiation of expression 3.105 yields
is controlled by the electron emission level the
differentiation of expression 3.105 yields
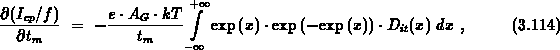
where we adopted several approximations mentioned above. The subintegral
function 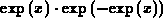 is sharply peaked at
is sharply peaked at 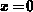 , as is
shown in Figure 3.9. The main contribution to the
integral comes from the region around
, as is
shown in Figure 3.9. The main contribution to the
integral comes from the region around 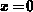 and the overall integral of this
function is
and the overall integral of this
function is 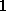 for the interval
for the interval 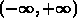 . Therefore, we may
approximate
. Therefore, we may
approximate
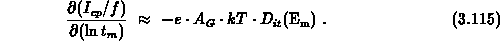
The level 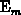 actually scanned is given
by 3.106. Formula 3.114 is
valid if
actually scanned is given
by 3.106. Formula 3.114 is
valid if 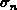 is not a function of energy
is not a function of energy 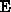 . This method has been
proposed in [154] and is in the standard use in engineering practice.
In the three-level technique,
. This method has been
proposed in [154] and is in the standard use in engineering practice.
In the three-level technique, 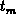 is controlled directly [377][206].
For the trapezoidal waveform,
is controlled directly [377][206].
For the trapezoidal waveform, 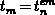 holds. When applying
relationship 3.115, it is usually assumed that
holds. When applying
relationship 3.115, it is usually assumed that
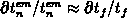 .
.
After applying method 3.115 on the numerical data
shown in Figure 3.10 we have obtained the trap
distributions presented in Figure 3.11. We have
also carried out the same procedure for an initially assumed uniform trap
distribution, which is shown in Figure 3.11 as well.
In both cases, the trapezoidal waveform is applied on the gate. Inspecting the
extracted versus the assumed distributions we conclude that the present
technique leads to an error in the amount of the traps density. Moreover, a
shift on the energy scale cannot be excluded as well. The errors could be
attributed to
- an improper
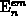 resulting from 3.66.
The variations in
resulting from 3.66.
The variations in 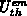 and
and 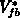 influence
influence 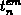 ,
thereby inducing an error in the calculation of the position
,
thereby inducing an error in the calculation of the position
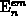 which is actually scanned.
which is actually scanned.
- an improper
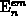 due to a step approximation of the
occupancy function.
due to a step approximation of the
occupancy function.
- an error when 3.115 is applied on the
trapezoidal pulses assuming the approximation
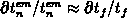 .
.
The first two effects shift the extracted trap distribution on the energy axis.
They cannot explain, however, the obtained underestimation in the level for
the uniform trap distribution. Henceforward, we discuss these explanations
in more detail.
The extracted trap densities depicted by 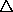 and
and  for the linear
and uniform distributions, respectively, are calculated by accounting for the
variation of
for the linear
and uniform distributions, respectively, are calculated by accounting for the
variation of 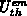 with
with 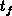 . The calculated
. The calculated 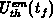 is
used in obtaining the emission time
is
used in obtaining the emission time 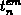 which is applied to determine
the scanned position
which is applied to determine
the scanned position 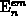 . For the data shown by
. For the data shown by  and
and
 the level
the level 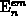 is calculated assuming
is calculated assuming 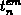 resulting
from the approximation
resulting
from the approximation 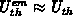 . Note that
. Note that
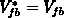 is used in all calculations. We conclude that the error in the
currently scanned position due to an inaccurate
is used in all calculations. We conclude that the error in the
currently scanned position due to an inaccurate 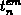 is small and cannot
account for the disagreement between the extracted and the assumed linear
distribution.
is small and cannot
account for the disagreement between the extracted and the assumed linear
distribution.
To estimate the error due to a finite width of the transition region in the
non-steady-state occupancy function we introduce a differential charge-pumping
current
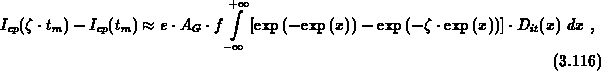
like the signal in DLTS measurements. The parameter 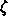 determine the
width of the time steps used in the charge-pumping measurements. Typically,
the current is measured in the subsequent moments
determine the
width of the time steps used in the charge-pumping measurements. Typically,
the current is measured in the subsequent moments 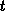 and
and 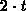 and
formula 3.115 is applied on finite differences.
The normalized subintegral function
and
formula 3.115 is applied on finite differences.
The normalized subintegral function
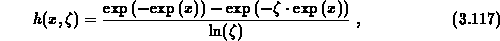
determines the width of the scanned region. This universal function is
independent of the actual time 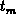 , but depends only on the time window.
The integral of
, but depends only on the time window.
The integral of 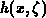 in the interval
in the interval 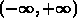 equals to
equals to
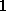 . By subtracting the occupancy functions in the two closely set moments
(e.g.
. By subtracting the occupancy functions in the two closely set moments
(e.g. 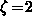 ) the long tails in the region
) the long tails in the region 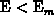 cancel each other, yielding a nearly symmetric function
cancel each other, yielding a nearly symmetric function 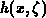 around
around
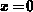 . The
. The 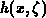 function is sharply peaked and its maximal
contribution to the integral comes from the region around the maximum at
function is sharply peaked and its maximal
contribution to the integral comes from the region around the maximum at
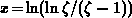 . For a common value
. For a common value 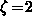 the
maximum is shifted by only
the
maximum is shifted by only 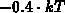 towards the lower energies from
towards the lower energies from
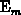 . In addition, the variations in the trap distribution can be
neglected within the window
. In addition, the variations in the trap distribution can be
neglected within the window 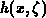 , also for rapidly changing
distributions in practice.
, also for rapidly changing
distributions in practice.
The disagreement in the amplitude for the uniform distribution clearly
originates from relationship 3.115. This
relationship is, however, correct, but its application to the trapezoidal
waveform introduces an error when
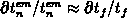 is assumed. In fact,
relationship 3.115 refers to the
is assumed. In fact,
relationship 3.115 refers to the
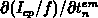 data. The measured data are
data. The measured data are
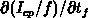 . The relation between the later two
data-sets is given over the factor
. The relation between the later two
data-sets is given over the factor 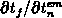 . For the
trapezoidal pulses it equals to
. For the
trapezoidal pulses it equals to
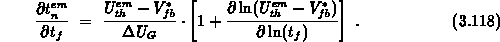
Finally, formula 3.115 yields for the trapezoidal
pulses
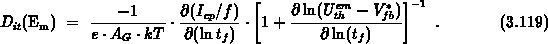
The second term in the brackets at the right-hand-side was always neglected.
This factor is negative. Therefore, the calculated trap distribution in the
energy space is lower when this factor is not accounted for. This effect is
responsible for an enhanced error when approaching the mid-gap and for a
strong underestimation in the trap density close to the band-edges.
Note that this effect does not exist in the three-level charge-pumping
measurements.




Next: 3.4 Geometric Current Component
Up: 3.3 Analytical Modeling of
Previous: Frequency-Dependence of the
Martin Stiftinger
Sat Oct 15 22:05:10 MET 1994
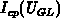 curve. In this region, the active energy interval contributing to the
current is determined by the non-steady-state emission levels of electrons
curve. In this region, the active energy interval contributing to the
current is determined by the non-steady-state emission levels of electrons
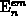 and holes
and holes 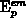 . In order to evaluate the error
introduced by a step approximation of the occupancy function we will discuss
the three-level gate waveform shown in Figure 3.3, instead of
the trapezoidal waveform. In the three-level technique the electron emission
time is exactly known and equals to the mid-level duration
. In order to evaluate the error
introduced by a step approximation of the occupancy function we will discuss
the three-level gate waveform shown in Figure 3.3, instead of
the trapezoidal waveform. In the three-level technique the electron emission
time is exactly known and equals to the mid-level duration 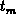 if the falling
edges are sufficiently abrupt (
if the falling
edges are sufficiently abrupt (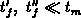 ). By considering the
three-level method, an eventual error in the determination of the emission time
). By considering the
three-level method, an eventual error in the determination of the emission time
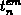 , which can result from an inaccurate
, which can result from an inaccurate 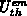 and
and 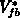 ,
is avoided. In the three-level method, it is assumed that all available traps
are filled by electrons at the top level and recombined by holes at the bottom
level. When the falling edges are abrupt the
,
is avoided. In the three-level method, it is assumed that all available traps
are filled by electrons at the top level and recombined by holes at the bottom
level. When the falling edges are abrupt the 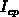 is given by
is given by




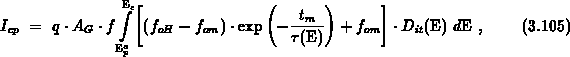
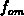 is the steady-state occupancy function at the mid level
is the steady-state occupancy function at the mid level
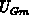 and
and 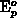 is the lower energy boundary
(
is the lower energy boundary
(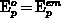 in the conditions of interest here).
We further assume
in the conditions of interest here).
We further assume 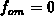 for traps of interest and a level
for traps of interest and a level 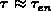 .
.
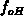 may also
be approximated by a step-like function at
may also
be approximated by a step-like function at 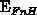 and
and 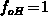 holds for traps of interest.
holds for traps of interest.
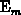 so that
so that
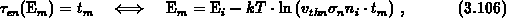
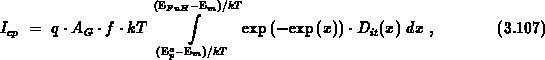
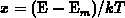 . The subintegral function
. The subintegral function
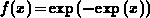 is the solution for the occupancy function
in the non-steady-state emission mode when
is the solution for the occupancy function
in the non-steady-state emission mode when
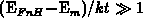 . A general solution, also valid for
short time intervals
. A general solution, also valid for
short time intervals 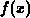 is independent of
is independent of 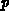 to an occupancy of
to an occupancy of 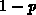 is given by
is given by
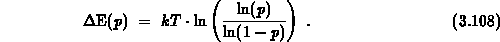
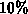 to
to 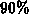 trap occupancy has a width
of
trap occupancy has a width
of 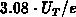 , which is not negligible with respect to the band gap.
, which is not negligible with respect to the band gap.
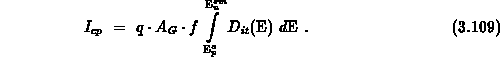
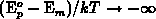 and
and
 . The emission level
. The emission level
 , where
, where
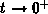 has
been discussed in
has
been discussed in 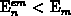 . It follows the equation with respect to
. It follows the equation with respect to
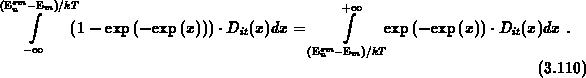
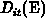 . A substitution of
. A substitution of
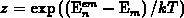 in
in 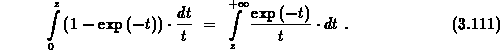
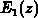 function,
whereas the left-hand-side is the
function,
whereas the left-hand-side is the 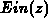 function (
function (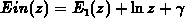 , where
, where
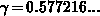 is the Euler constant, one obtains
is the Euler constant, one obtains
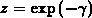 for the solution of
for the solution of 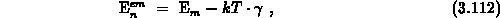
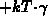 . The
. The 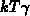 shift is small, but not negligible in comparison with the active energy
interval which is less than
shift is small, but not negligible in comparison with the active energy
interval which is less than 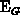 . When accounting for both, the
electron and the hole non-steady-state emission the reduction of the active
energy interval becomes
. When accounting for both, the
electron and the hole non-steady-state emission the reduction of the active
energy interval becomes 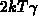 , which is
, which is 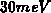 at room temperature.
This can result in
at room temperature.
This can result in 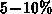 reduction in
reduction in 
 interfaces
interfaces 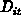 can significantly vary with energy
along the forbidden band, particularly close to the band edges. To estimate
the correction of
can significantly vary with energy
along the forbidden band, particularly close to the band edges. To estimate
the correction of 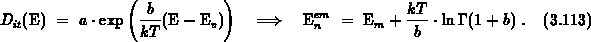
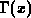 is the Gamma function. The factor
is the Gamma function. The factor
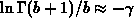 for small
for small 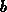 , which is a typical case
in practice. For example, assuming a variation of the trap density in the
upper half of the band gap so that
, which is a typical case
in practice. For example, assuming a variation of the trap density in the
upper half of the band gap so that
 at the mid-gap and
at the mid-gap and
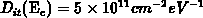 at the band edge, it
follows
at the band edge, it
follows 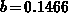 and
and 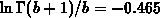 . Therefore, an
exponentially varying
. Therefore, an
exponentially varying 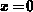 where the occupancy
function
where the occupancy
function 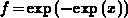 changes rapidly. As a conclusion, the
correction
changes rapidly. As a conclusion, the
correction 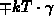 is a valid approximation in all cases of
practical interest.
is a valid approximation in all cases of
practical interest.
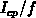 over
over 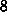 decades of
the fall and rise times. The calculated family of the curves is shown in
Figure
decades of
the fall and rise times. The calculated family of the curves is shown in
Figure 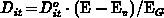 and is shown in
Figure
and is shown in
Figure 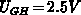 to strong accumulation at
to strong accumulation at
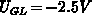 . In this case,
. In this case, 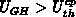 and
and
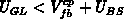 are fulfilled for all
are fulfilled for all 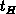 and
and 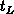 , including
the shortest considered (see Figure
, including
the shortest considered (see Figure 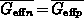 , because of a very
large geometric component occurring in
, because of a very
large geometric component occurring in 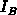 for
for 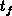 in the
in the 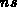 -range. Note
that the frequency applied in the calculations is unacceptably high for
-range. Note
that the frequency applied in the calculations is unacceptably high for
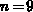 and low for
and low for 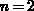 and
and 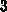 , regarding practical measurements.
In all analytical calculations we adopt
, regarding practical measurements.
In all analytical calculations we adopt 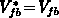 and
and
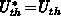 .
.
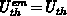 and
and
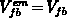 the analytical model remarkably overestimates
the analytical model remarkably overestimates 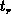 in the
in the  -range (these results are not shown here). In a
better approach
-range (these results are not shown here). In a
better approach 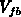 are calculated for a specified
are calculated for a specified 
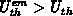 holds, which results in a longer
holds, which results in a longer
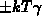 is taken into account the
agreement with the numerical result is excellent in the sub-
is taken into account the
agreement with the numerical result is excellent in the sub-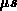 range
(dotted curves which are shown for some time decades). However, the
range
(dotted curves which are shown for some time decades). However, the 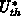 with
with 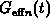 and
and 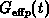 , during the fall edge of
the gate pulse we found that
, during the fall edge of
the gate pulse we found that 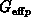 becomes dominant over
becomes dominant over
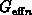 at
at 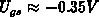 for
for 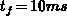 and at
and at
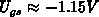 for
for 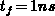 . However, while in the case for
. However, while in the case for
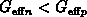 until the level
until the level 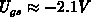 is
exceeded. Moreover, the study of the geometric component presented in
Section
is
exceeded. Moreover, the study of the geometric component presented in
Section 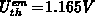 and
and 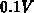 for
for 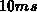 , respectively. The device voltages are
, respectively. The device voltages are
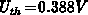 and
and 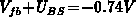 . Consequently, the
variation of
. Consequently, the
variation of 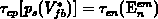 . It is a trivial task
to reduce the problem to a coupled system of two implicit algebraic equations,
which can be simply solved. These results will be presented in a further study.
. It is a trivial task
to reduce the problem to a coupled system of two implicit algebraic equations,
which can be simply solved. These results will be presented in a further study.
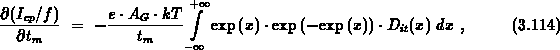
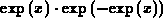 is sharply peaked at
is sharply peaked at 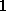 for the interval
for the interval 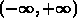 . Therefore, we may
approximate
. Therefore, we may
approximate
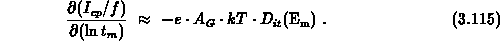
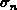 is not a function of energy
is not a function of energy 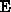 . This method has been
proposed in
. This method has been
proposed in 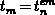 holds. When applying
relationship
holds. When applying
relationship 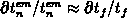 .
.
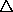 and
and  for the linear
and uniform distributions, respectively, are calculated by accounting for the
variation of
for the linear
and uniform distributions, respectively, are calculated by accounting for the
variation of 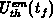 is
used in obtaining the emission time
is
used in obtaining the emission time  and
and
 the level
the level 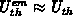 . Note that
. Note that
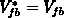 is used in all calculations. We conclude that the error in the
currently scanned position due to an inaccurate
is used in all calculations. We conclude that the error in the
currently scanned position due to an inaccurate 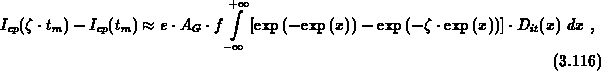
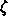 determine the
width of the time steps used in the charge-pumping measurements. Typically,
the current is measured in the subsequent moments
determine the
width of the time steps used in the charge-pumping measurements. Typically,
the current is measured in the subsequent moments 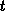 and
and 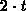 and
formula
and
formula 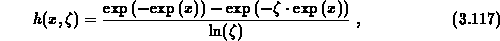

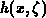 in the interval
in the interval 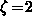 ) the long tails in the region
) the long tails in the region 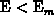 cancel each other, yielding a nearly symmetric function
cancel each other, yielding a nearly symmetric function 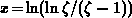 . For a common value
. For a common value 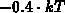 towards the lower energies from
towards the lower energies from
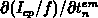 data. The measured data are
data. The measured data are
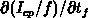 . The relation between the later two
data-sets is given over the factor
. The relation between the later two
data-sets is given over the factor 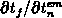 . For the
trapezoidal pulses it equals to
. For the
trapezoidal pulses it equals to