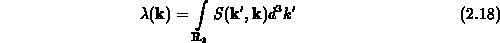2.1.1 Ableitung der Boltzmanngleichung




Next: 2.1.2 Gültigkeit der Boltzmanngleichung
Up: 2.1 Die Boltzmanngleichung
Previous: 2.1 Die Boltzmanngleichung
Ein kinetisches System besteht aus Teilchen in einem fest definierten Volumen
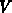 , dessen physikalischen Eigenschaften sich zeitlich ändern und untersucht
werden sollen. Diese Partikel erfahren aber Zusammenstöße und unterliegen dem
Einfluß äußerer Kräfte, wobei eine Änderung des Teilchenzustands
hervorgerufen wird. Die Energie, die aufgrund von Wechselwirkungen ausgetauscht
werden kann, sei jedoch gering. Eine weitere Forderung besteht darin, daß die
Wellenpakete der untersuchten Teilchen lokalisiert sein müssen, daß also deren
Ausdehnung kleiner als der mittlere Teilchenabstand ist. Die
de-Broglie-Wellenlänge
, dessen physikalischen Eigenschaften sich zeitlich ändern und untersucht
werden sollen. Diese Partikel erfahren aber Zusammenstöße und unterliegen dem
Einfluß äußerer Kräfte, wobei eine Änderung des Teilchenzustands
hervorgerufen wird. Die Energie, die aufgrund von Wechselwirkungen ausgetauscht
werden kann, sei jedoch gering. Eine weitere Forderung besteht darin, daß die
Wellenpakete der untersuchten Teilchen lokalisiert sein müssen, daß also deren
Ausdehnung kleiner als der mittlere Teilchenabstand ist. Die
de-Broglie-Wellenlänge 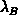 muß also folgende Ungleichung
muß also folgende Ungleichung
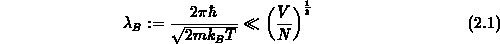
erfüllen, da sonst nur eine ausschließlich quantenmechanische Betrachtung
möglich ist. Man betrachtet also Teilchen bei hohen Temperaturen 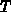 oder
niedriger Teilchenzahl
oder
niedriger Teilchenzahl 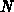 . Dabei stellt
. Dabei stellt 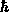 das reduzierte Planck'sche
Wirkungsquantum,
das reduzierte Planck'sche
Wirkungsquantum, 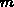 die Masse des Teilchens und
die Masse des Teilchens und 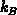 die Boltzmannkonstante
dar. Damit kann allen Teilchen sowohl ein Ort als auch ein Impuls und somit eine
Geschwindigkeit hinreichend genau zugeordnet werden, und Ort und Impuls können
unabhängig voneinander betrachtet werden. Wenn diese Forderung erfüllt ist,
dann wird, kann ein System mit den klassischen Gesetzmäßigkeiten analysiert
werden. Des weiteren wird ein System untersucht, bei dem nur eine einzige
Teilchenart betrachtet werden muß, um die mathematische Ableitung möglichst
einfach beschreiben zu können.
die Boltzmannkonstante
dar. Damit kann allen Teilchen sowohl ein Ort als auch ein Impuls und somit eine
Geschwindigkeit hinreichend genau zugeordnet werden, und Ort und Impuls können
unabhängig voneinander betrachtet werden. Wenn diese Forderung erfüllt ist,
dann wird, kann ein System mit den klassischen Gesetzmäßigkeiten analysiert
werden. Des weiteren wird ein System untersucht, bei dem nur eine einzige
Teilchenart betrachtet werden muß, um die mathematische Ableitung möglichst
einfach beschreiben zu können.
Die makroskopischen Eigenschaften eines physikalischen Systems werden bestimmt,
indem man die Bewegung aller Teilchen verfolgt. Dies ist jedoch praktisch nicht
möglich, da dabei die Bewegungsgleichung für jedes einzelne Teilchen berechnet
werden muß und zusätzlich noch die Anfangsbedingungen für jedes einzelne
Teilchen bekannt sein müssen. Man ist daher gezwungen, statistische Methoden
zur Beschreibung des zeitlichen Verhaltens eines makroskopischen Systems zu
gebrauchen. Statt der Bewegung eines einzelnen Partikels verfolgt man nun das
zeitliche Verhalten der Verteilungsfunktion 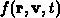 in
Abhängigkeit des Orts
in
Abhängigkeit des Orts  , der Geschwindigkeit
, der Geschwindigkeit 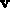 und der Zeit
und der Zeit
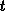 , die im sechsdimensionalen Volumenelement
, die im sechsdimensionalen Volumenelement 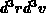 die mittlere Anzahl der
Teilchen
die mittlere Anzahl der
Teilchen 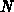
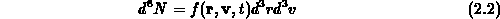
angibt. Diese mittlere Anzahl an Teilchen ist nun als Integral der
Teilchendichte über das räumliche Volumen 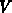 und die Geschwindigkeit
definiert,
und die Geschwindigkeit
definiert,
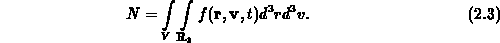
Eine orts- und zeitabhängige Teilchendichte 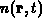 erhält
man durch Mittelung über die Geschwindigkeit,
erhält
man durch Mittelung über die Geschwindigkeit,
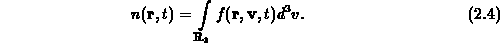
Man kann den Mittelwert 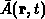 einer beliebigen
physikalischen Größe
einer beliebigen
physikalischen Größe 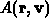 bei Kenntnis der
Verteilungsfunktion mittels Integration über die Geschwindigkeit berechnen,
bei Kenntnis der
Verteilungsfunktion mittels Integration über die Geschwindigkeit berechnen,
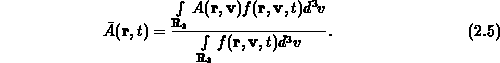
Mit derartigen Mittelwerten kann also auch ein System, das sich
nicht im Gleichgewichtszustand befindet, beschrieben werden, vorausgesetzt, daß
die Verteilungsfunktion bekannt ist.
Um die Verteilungsfunktion zu bestimmen, sollen vorderhand keine Kollisionen
der Teilchen berücksichtigt werden. Dann wird sich die Lage dieser
Funktion nach einem Zeitschritt 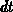 um
um
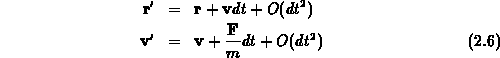
ändern, wobei 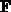 eine geschwindigkeitsunabhängige äußere Kraft
darstellt. Unter der getroffenen Annahme, daß keine Stöße stattfinden,
werden sich alle
Teilchen, die sich zur Zeit
eine geschwindigkeitsunabhängige äußere Kraft
darstellt. Unter der getroffenen Annahme, daß keine Stöße stattfinden,
werden sich alle
Teilchen, die sich zur Zeit 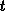 im Phasenraum innerhalb
im Phasenraum innerhalb 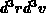 befinden, zum Zeitpunkt
befinden, zum Zeitpunkt 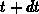 im sechsdimensionalen Volumen
im sechsdimensionalen Volumen 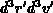 anzutreffen sein. Dieser Sachverhalt kann mathematisch folgendermaßen
anzutreffen sein. Dieser Sachverhalt kann mathematisch folgendermaßen
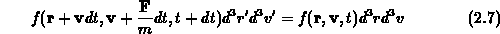
ausgedrückt werden. Das Volumenelement 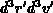 kann als
Funktionaldeterminante
kann als
Funktionaldeterminante
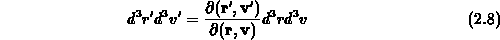
geschrieben werden, wenn die Koordinatentransformation von
Gleichung 2.6 verwendet wird. Die Auswertung der Funktionaldeterminante
ergibt,
daß diese einschließlich der Glieder erster Ordnung in 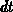 gleich eins
ist,
gleich eins
ist,
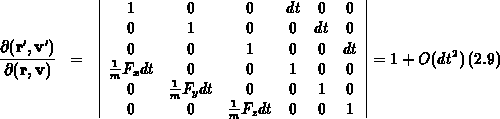
Nach einem Zeitschritt ist also die Verteilungsfunktion unverändert,
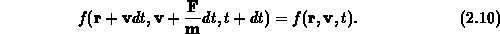
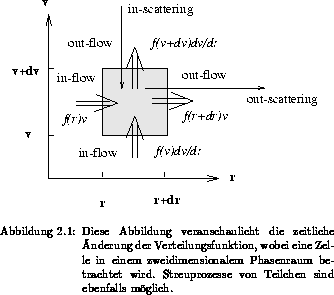
Treten aber noch zusätzlich Stöße auf, dann kommen nicht alle Teilchen, die
zum Zeitpunkt t im Phasenraum 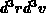 enthalten sind, in das zeitlich
weiterbewegte Volumen
enthalten sind, in das zeitlich
weiterbewegte Volumen 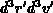 , sondern werden durch Kollisionen in andere
Phasenvolumenelemente gestreut, beziehungsweise können Teilchen durch
Streuprozesse in dem neuen, zeitlich veränderten infinitesimalen Element
enthalten
sein. Dieser Sachverhalt ist in Abbildung 2.1 dargestellt. Um diese
damit hervorgerufene Partikelschwankung zu berücksichtigen, wird ein
sogenannter Stoßterm
, sondern werden durch Kollisionen in andere
Phasenvolumenelemente gestreut, beziehungsweise können Teilchen durch
Streuprozesse in dem neuen, zeitlich veränderten infinitesimalen Element
enthalten
sein. Dieser Sachverhalt ist in Abbildung 2.1 dargestellt. Um diese
damit hervorgerufene Partikelschwankung zu berücksichtigen, wird ein
sogenannter Stoßterm 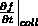
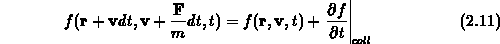
definiert. Nun entwickelt man die linke Seite dieser Gleichung nach 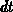 , wobei
anschließend
, wobei
anschließend 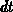 gegen Null streben soll. Die daraus resultierende
Gleichung stellt
die Bewegungsgleichung für die Verteilungsfunktion dar, wenn der Stoßterm
explizit angegeben wird. Diese Gleichung wird als Boltzmanngleichung bezeichnet
gegen Null streben soll. Die daraus resultierende
Gleichung stellt
die Bewegungsgleichung für die Verteilungsfunktion dar, wenn der Stoßterm
explizit angegeben wird. Diese Gleichung wird als Boltzmanngleichung bezeichnet
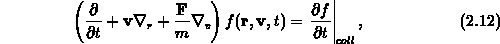
und findet in der Transporttheorie vielfach Anwendung. Die Operatoren
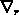 und
und 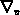 stellen den Gradienten in bezug auf den Ort
beziehungsweise nach der Geschwindigkeit dar.
stellen den Gradienten in bezug auf den Ort
beziehungsweise nach der Geschwindigkeit dar.
Um auch eine semiklassische Näherung der Quantenmechanik miteinzubeziehen, wird
der klassische Impuls durch den Kristallimpuls zu ersetzt. Der Wellenvektor
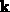 des Kristallimpulses wird nun als
des Kristallimpulses wird nun als
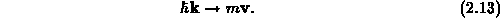
geschrieben. Man erhält dann die Boltzmanngleichung in Abhängigkeit des
Wellenvektors,
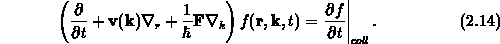
Dies ist nun diejenige Form, die zur
Charakterisierung von Nichtgleichgewichtsprozessen der Festkörperphysik
herangezogen wird [17].
Der sogenannte Streuterm wird unter Berücksichtigung der quantenmechanischen,
differentiellen Streuwahrscheinlichkeit 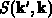 als
als
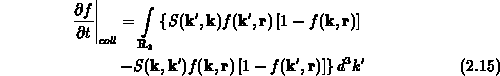
geschrieben. Die Streuwahrscheinlichkeit kann so interpretiert werden, daß ein
Teilchen mit Zustand 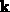 nach
nach 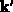 gestreut wird. Der Streuterm
dagegen wird als Differenz zwischen eintretenden und austretenden Teilchen im
Impulsvolumenelement
gestreut wird. Der Streuterm
dagegen wird als Differenz zwischen eintretenden und austretenden Teilchen im
Impulsvolumenelement 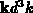 aufgefaßt. Die Annahme betreffs dieses
Streuterms beinhaltet nur Zweierstöße. Da in einem Halbleiter Kollisionen
dreier oder mehrerer Partikel
aufgefaßt. Die Annahme betreffs dieses
Streuterms beinhaltet nur Zweierstöße. Da in einem Halbleiter Kollisionen
dreier oder mehrerer Partikel eine sehr geringe Wahrscheinlichkeit aufweisen, erscheint
diese Näherung gerechtfertigt. Eine weitere Vereinfachung des Stoßterm ergibt
sich unter der Annahme, daß sich die Fermikante weder in der Nähe noch
überhalb des Leitungsbandes befindet und nur schwache Konzentrationen der
betrachteten Teilchenart vorliegen. Dies ist bei schwacher bis mittlerer
Dotierung zulässig. Damit kann auch das Pauliverbot,
eine sehr geringe Wahrscheinlichkeit aufweisen, erscheint
diese Näherung gerechtfertigt. Eine weitere Vereinfachung des Stoßterm ergibt
sich unter der Annahme, daß sich die Fermikante weder in der Nähe noch
überhalb des Leitungsbandes befindet und nur schwache Konzentrationen der
betrachteten Teilchenart vorliegen. Dies ist bei schwacher bis mittlerer
Dotierung zulässig. Damit kann auch das Pauliverbot,
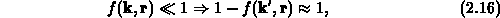
das eine doppelte Besetzung eines Elektronenzustands nicht zuläßt,
vernachlässigt werden, und man kann den Stoßterm linear in der
Verteilungsfunktion
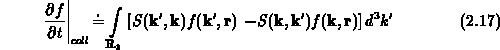
anschreiben. Die totale Streurate 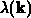 ist nun folgendermaßen
ist nun folgendermaßen
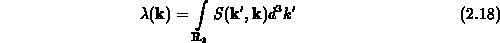
definiert. Das Pauliprinzip wird nur bei stark entarteten Halbleitermaterialien
berücksichtigt, die fast schon metallische Eigenschaften aufweisen.




Next: 2.1.2 Gültigkeit der Boltzmanngleichung
Up: 2.1 Die Boltzmanngleichung
Previous: 2.1 Die Boltzmanngleichung
Martin Stiftinger
Mon Aug 7 18:44:55 MET DST 1995
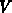 , dessen physikalischen Eigenschaften sich zeitlich ändern und untersucht
werden sollen. Diese Partikel erfahren aber Zusammenstöße und unterliegen dem
Einfluß äußerer Kräfte, wobei eine Änderung des Teilchenzustands
hervorgerufen wird. Die Energie, die aufgrund von Wechselwirkungen ausgetauscht
werden kann, sei jedoch gering. Eine weitere Forderung besteht darin, daß die
Wellenpakete der untersuchten Teilchen lokalisiert sein müssen, daß also deren
Ausdehnung kleiner als der mittlere Teilchenabstand ist. Die
de-Broglie-Wellenlänge
, dessen physikalischen Eigenschaften sich zeitlich ändern und untersucht
werden sollen. Diese Partikel erfahren aber Zusammenstöße und unterliegen dem
Einfluß äußerer Kräfte, wobei eine Änderung des Teilchenzustands
hervorgerufen wird. Die Energie, die aufgrund von Wechselwirkungen ausgetauscht
werden kann, sei jedoch gering. Eine weitere Forderung besteht darin, daß die
Wellenpakete der untersuchten Teilchen lokalisiert sein müssen, daß also deren
Ausdehnung kleiner als der mittlere Teilchenabstand ist. Die
de-Broglie-Wellenlänge 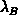 muß also folgende Ungleichung
muß also folgende Ungleichung




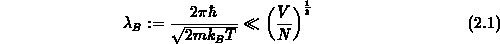
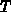 oder
niedriger Teilchenzahl
oder
niedriger Teilchenzahl 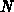 . Dabei stellt
. Dabei stellt 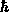 das reduzierte Planck'sche
Wirkungsquantum,
das reduzierte Planck'sche
Wirkungsquantum, 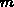 die Masse des Teilchens und
die Masse des Teilchens und 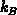 die Boltzmannkonstante
dar. Damit kann allen Teilchen sowohl ein Ort als auch ein Impuls und somit eine
Geschwindigkeit hinreichend genau zugeordnet werden, und Ort und Impuls können
unabhängig voneinander betrachtet werden. Wenn diese Forderung erfüllt ist,
dann wird, kann ein System mit den klassischen Gesetzmäßigkeiten analysiert
werden. Des weiteren wird ein System untersucht, bei dem nur eine einzige
Teilchenart betrachtet werden muß, um die mathematische Ableitung möglichst
einfach beschreiben zu können.
die Boltzmannkonstante
dar. Damit kann allen Teilchen sowohl ein Ort als auch ein Impuls und somit eine
Geschwindigkeit hinreichend genau zugeordnet werden, und Ort und Impuls können
unabhängig voneinander betrachtet werden. Wenn diese Forderung erfüllt ist,
dann wird, kann ein System mit den klassischen Gesetzmäßigkeiten analysiert
werden. Des weiteren wird ein System untersucht, bei dem nur eine einzige
Teilchenart betrachtet werden muß, um die mathematische Ableitung möglichst
einfach beschreiben zu können.
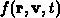 in
Abhängigkeit des Orts
in
Abhängigkeit des Orts  , der Geschwindigkeit
, der Geschwindigkeit 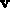 und der Zeit
und der Zeit
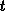 , die im sechsdimensionalen Volumenelement
, die im sechsdimensionalen Volumenelement 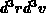 die mittlere Anzahl der
Teilchen
die mittlere Anzahl der
Teilchen 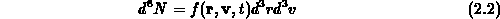
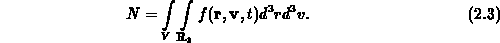
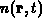 erhält
man durch Mittelung über die Geschwindigkeit,
erhält
man durch Mittelung über die Geschwindigkeit,
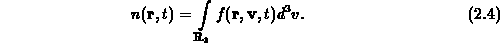
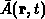 einer beliebigen
physikalischen Größe
einer beliebigen
physikalischen Größe 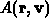 bei Kenntnis der
Verteilungsfunktion mittels Integration über die Geschwindigkeit berechnen,
bei Kenntnis der
Verteilungsfunktion mittels Integration über die Geschwindigkeit berechnen,
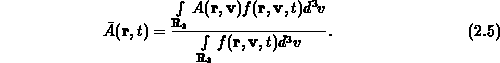
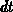 um
um
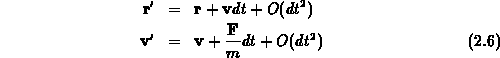
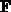 eine geschwindigkeitsunabhängige äußere Kraft
darstellt. Unter der getroffenen Annahme, daß keine Stöße stattfinden,
werden sich alle
Teilchen, die sich zur Zeit
eine geschwindigkeitsunabhängige äußere Kraft
darstellt. Unter der getroffenen Annahme, daß keine Stöße stattfinden,
werden sich alle
Teilchen, die sich zur Zeit 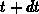 im sechsdimensionalen Volumen
im sechsdimensionalen Volumen 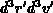 anzutreffen sein. Dieser Sachverhalt kann mathematisch folgendermaßen
anzutreffen sein. Dieser Sachverhalt kann mathematisch folgendermaßen
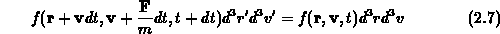
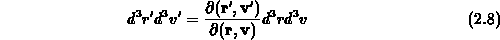
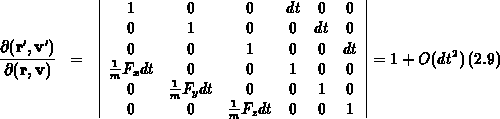
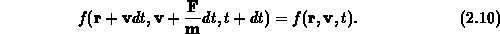

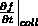
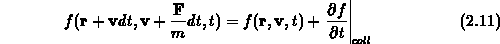
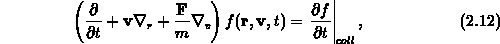
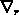 und
und 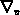 stellen den Gradienten in bezug auf den Ort
beziehungsweise nach der Geschwindigkeit dar.
stellen den Gradienten in bezug auf den Ort
beziehungsweise nach der Geschwindigkeit dar.
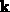 des Kristallimpulses wird nun als
des Kristallimpulses wird nun als
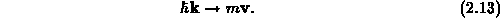
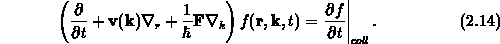
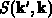 als
als
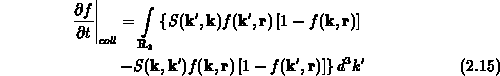
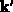 gestreut wird. Der Streuterm
dagegen wird als Differenz zwischen eintretenden und austretenden Teilchen im
Impulsvolumenelement
gestreut wird. Der Streuterm
dagegen wird als Differenz zwischen eintretenden und austretenden Teilchen im
Impulsvolumenelement 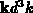 aufgefaßt. Die Annahme betreffs dieses
Streuterms beinhaltet nur Zweierstöße. Da in einem Halbleiter Kollisionen
dreier oder mehrerer Partikel
aufgefaßt. Die Annahme betreffs dieses
Streuterms beinhaltet nur Zweierstöße. Da in einem Halbleiter Kollisionen
dreier oder mehrerer Partikel
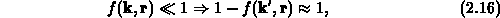
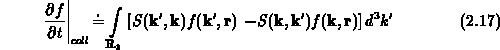
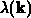 ist nun folgendermaßen
ist nun folgendermaßen