6.3 Konvergenzverhalten, Abschätzung des Simulationsfehlers

Abbildung 6.4 und 6.5 geben einen Detailausschnitt des Konvergenzverhaltens für die Berechnung der Gegeninduktivität bzw. der Selbstinduktivität wieder. Beide Kurven zeigen deutlich die stetige Verkleinerung der Schwankungsbreite, die in Abb. 6.4 rascher als in Abb. 6.5 vor sich geht. Da im Fall der Gegeninduktivität die Varianz kleiner ist, genügen weniger Stichproben als für die Selbstinduktivität, um die gleiche Genauigkeit zu erreichen. Dies ist auf den Term 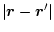$\vert\mathchoice{\mbox{\boldmath $\displaystyle r$}} {\mbox{\boldmath $\textst... ...ox{\boldmath $\scriptstyle r$}} {\mbox{\boldmath $\scriptscriptstyle r$}}'\vert$ im Nenner zurückzuführen. Die Auswertung der Gegeninduktivität ist durch einen größeren Abstand gekennzeichnet, deshalb schwankt der auszuwertende Integrand nicht in diesem Ausmaß wie für die Selbstinduktivität.

**Abbildung 6.4:** Darstellung der berechneten Gegeninduktivität des planaren Transformators mit 3 Windungen in Abhängigkeit der Stichprobenanzahl
$\begin{figure}{\resizebox{0.86\textwidth}{!}{\includegraphics[{}]{MC3conv}}}\end{figure}$

**Abbildung 6.5:** Darstellung der berechneten Selbstinduktivität des planaren Transformators mit 3 Windungen in Abhängigkeit der Stichprobenanzahl
$\begin{figure}{\resizebox{0.86\textwidth}{!}{\includegraphics[{}]{LC3conv}}}\end{figure}$

Fehlerquellen in der Berechnung der Induktivitäten sind sowohl auf die Stromdichteverteilung als auch auf die Monte Carlo Methode zurückzuführen. Diese voneinander unabhängigen Fehlerquellen können separat behandelt werden. Um den Einfluss von Stromdichteungenauigkeiten zu minimieren, können Gitterverfeinerungstechniken eingesetzt werden. Entsprechend den Änderungen der berechneten Induktivitäten kann nur ein differentieller und kein absoluter Fehler angegeben werden (es sei denn man vergleicht mit analytischen Lösungen).

Da die Fehlerabschätzung für die Monte Carlo Methode ohne großen Aufwand mit den Gleichungen (6.1) und (6.2) durchzuführen ist, erscheint die Vorgabe eines Abbruchkriteriums sinnvoll, das den Monte Carlo Algorithmus beendet, wenn die verfahrensbedingten Schwankungen eine vorgegebene Schranke unterschreiten. Der zentrale Grenzwertsatz besagt, dass der EW normal verteilt ist, falls die Stichprobenzahl N groß ist^6.1. 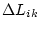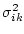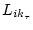Der Fehler der Resultate $\Delta L_{ik}$ kann daher über die Varianz $\sigma^2_{ik}$ der Stichprobenauswertung $L_{ik_\tau}$

$\displaystyle \sigma^2_{ik}$

$\displaystyle =\frac{1}{N}\sum_{\tau} L_{ik_\tau}^2-\Big(\frac{1}{N}\sum_{\tau} L_{ik_\tau}\Big)^2$

(6.1)

und die Stichprobenanzahl N (99.99 % Konfidenzintervall)

$\displaystyle \Delta L_{ik}$

$\displaystyle =3\frac{\sigma_{ik}}{\sqrt{N}}$

(6.2)

ermittelt werden. Die Monte Carlo Methode mit Abbruchkriterium bedarf nur der Erweiterung um die kontinuierliche Berechnung der Standardabweichung von den ermittelten Werten aus (6.2) mittels (6.1). Sobald 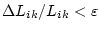$\Delta L_{ik}/L_{ik} < \varepsilon$ erfüllt ist, wird der Algorithmus beendet. Die Fehlerschranke des Schätzwertes fällt mit 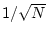$1/\sqrt{N}$ . Will man also die Fehlerschranke um einen Faktor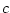

reduzieren, so steigt die erforderliche Zahl der Zufallsversuche und damit der Rechenaufwand mit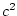

Fußnoten

... ist ^6.1: Über die Geschwindigkeit der Konvergenz gibt der zentrale Grenzwertsatz keine Auskunft, sondern die Varianz, die linear mit der Stichprobenanzahl gegen 0 geht.

C. Harlander: Numerische Berechnung von Induktivitäten in dreidimensionalen Verdrahtungsstrukturen