3.2 Extensions of the Reaction-Diffusion Model
The lack of a decent description of recovery based on the reaction-diffusion
theory, cf. (3.2), soon urged the development of modified and extended RD
models [63, 33, 64, 41, 17, 59, 65, 66, 67, 55]. In the following variants thereof
are summarized.
- As modern oxide layers are only a few nanometers thick, the
explanation based on diffusing hydrogen inside the oxide was
questioned. Therefore the diffusion process of
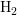 was suggested to
continue inside the polysilicon as well [63]. By assuming two different
diffusion coefficients, namely fast diffusion in the oxide and slow
diffusion inside the polysilicon, the so-called two-region RD model
was expected to be able to explain the much larger observed recovery
range. Actually this range only increased at little [55].
was suggested to
continue inside the polysilicon as well [63]. By assuming two different
diffusion coefficients, namely fast diffusion in the oxide and slow
diffusion inside the polysilicon, the so-called two-region RD model
was expected to be able to explain the much larger observed recovery
range. Actually this range only increased at little [55].
- The two-interface RD model [33], presented by Krishnan et al.,
focuses on the quick diffusion of atomic hydrogen inside the oxide.
Once having reached the polysilicon interface, a second chemical
reaction takes place creating molecular hydrogen (
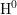
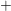
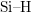
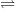
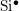
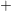
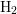 ). Like in the two-region model, the molecular hydrogen
diffuses further into the polysilicon. Since the diffusivity in the oxide is
regarded to be very high compared to the diffusivity in the polysilicon,
the
). Like in the two-region model, the molecular hydrogen
diffuses further into the polysilicon. Since the diffusivity in the oxide is
regarded to be very high compared to the diffusivity in the polysilicon,
the 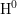 stored in the oxide is indeed able to cause a fast initial
recovery. For large stress times, on the other hand, it is this higher
oxide diffusivity that locks the hydrogen in the polysilicon for a long
time. This means that the short recovery effect vanishes.
stored in the oxide is indeed able to cause a fast initial
recovery. For large stress times, on the other hand, it is this higher
oxide diffusivity that locks the hydrogen in the polysilicon for a long
time. This means that the short recovery effect vanishes.
- In contrast to the two-region RD model, where instant dimerization at
the interface is assumed, the RD model with explicit dimerization
is based on a continuous dimerization process inside the oxide, what
allows both hydrogen species to coexist while diffusing into the oxide
[64]. Whereas the initial stress phase is thereby altered to
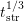 , the
recovery characteristic remains the same compared to the standard
RD model.
, the
recovery characteristic remains the same compared to the standard
RD model.
- Since the experimentally observed recovery revealed a log-like
characteristics (cf. Section 4.1), Islam et al. questioned the interface
states to be fast enough to follow the gate voltage
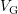 switches.
They suggested an RD model assuming slow interface states.
Unfortunately, such a model is in stark contradiction to the
Shockley-Read-Hall theory (SRH) used to describe the trapping
dynamics at the interface with transients due to electron capture being
within the nano-second regime. Under the assumption of exessively
small capture cross sections some sort of fast relaxation in the
microsecond-regime within one or two decades in time is indeed
obtained. However, this form of recovery is not observed in any
experimental data [55].
switches.
They suggested an RD model assuming slow interface states.
Unfortunately, such a model is in stark contradiction to the
Shockley-Read-Hall theory (SRH) used to describe the trapping
dynamics at the interface with transients due to electron capture being
within the nano-second regime. Under the assumption of exessively
small capture cross sections some sort of fast relaxation in the
microsecond-regime within one or two decades in time is indeed
obtained. However, this form of recovery is not observed in any
experimental data [55].
- Extended reaction-dispersive-diffusion (RDD) models using a
broad distribution of energy levels were discussed in [17, 59, 65, 66,
55]. They describe the hydrogen transport occuring via the highest
energetic states only (transport level). Hydrogen being located in a
deeper energy level needs to be thermally activated prior to be able to
diffuse further into or out of the oxide, i.e. without any activation this
hydrogen is trapped. Further, in these models only hydrogen sitting at
the interface is allowed to re-passivate which slows down the reverse
rate as most of the hydrogen is trapped.
In contrast, a simplified version of the RDD model does not
differentiate between trapped and untrapped hydrogen, i.e. all
hydrogen is allowed to interact with the interface [67]. This implies a
faster initial recovery, compared to the non-simplified RDD model, cf.
simulations performed in [55].
Although with increasing dispersion of the bond breaking at the
interface the recovery can be slowed down, none of the RDD variants
is finally able to describe the actual experiment.
The following conclusion can be drawn for RD theory in general. While
during recovery solely passivation occurs, the stress is modeled using
depassivation and passivation simultaneously [31]. At present, no extension of the
RD-model is able to describe recovery after stress in a reasonable form. Whether
such a model is then able to describe the much more complex stress-relaxation
patterns during the operation of a MOSFET is very questionable. The
premises are simply not correct. This leads to the conclusion that hydrogen
diffusion is very unlikely to be a main player when dealing with NBTI
degradation. For this reason completely new approaches are inevitable
[11, 6, 40, 61, 68, 69, 18].
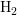 was suggested to
continue inside the polysilicon as well [63]. By assuming two different
diffusion coefficients, namely fast diffusion in the oxide and slow
diffusion inside the polysilicon, the so-called two-region RD model
was expected to be able to explain the much larger observed recovery
range. Actually this range only increased at little [55].
was suggested to
continue inside the polysilicon as well [63]. By assuming two different
diffusion coefficients, namely fast diffusion in the oxide and slow
diffusion inside the polysilicon, the so-called two-region RD model
was expected to be able to explain the much larger observed recovery
range. Actually this range only increased at little [55].
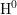
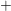
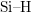
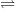
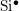
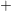
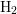 ). Like in the two-region model, the molecular hydrogen
diffuses further into the polysilicon. Since the diffusivity in the oxide is
regarded to be very high compared to the diffusivity in the polysilicon,
the
). Like in the two-region model, the molecular hydrogen
diffuses further into the polysilicon. Since the diffusivity in the oxide is
regarded to be very high compared to the diffusivity in the polysilicon,
the 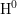 stored in the oxide is indeed able to cause a fast initial
recovery. For large stress times, on the other hand, it is this higher
oxide diffusivity that locks the hydrogen in the polysilicon for a long
time. This means that the short recovery effect vanishes.
stored in the oxide is indeed able to cause a fast initial
recovery. For large stress times, on the other hand, it is this higher
oxide diffusivity that locks the hydrogen in the polysilicon for a long
time. This means that the short recovery effect vanishes.
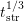 , the
recovery characteristic remains the same compared to the standard
RD model.
, the
recovery characteristic remains the same compared to the standard
RD model.
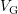 switches.
They suggested an RD model assuming slow interface states.
Unfortunately, such a model is in stark contradiction to the
Shockley-Read-Hall theory (SRH) used to describe the trapping
dynamics at the interface with transients due to electron capture being
within the nano-second regime. Under the assumption of exessively
small capture cross sections some sort of fast relaxation in the
microsecond-regime within one or two decades in time is indeed
obtained. However, this form of recovery is not observed in any
experimental data [55].
switches.
They suggested an RD model assuming slow interface states.
Unfortunately, such a model is in stark contradiction to the
Shockley-Read-Hall theory (SRH) used to describe the trapping
dynamics at the interface with transients due to electron capture being
within the nano-second regime. Under the assumption of exessively
small capture cross sections some sort of fast relaxation in the
microsecond-regime within one or two decades in time is indeed
obtained. However, this form of recovery is not observed in any
experimental data [55].