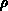 (siehe auch Gleichung (3.104))
vom elektrostatischen Potential
(siehe auch Gleichung (3.104))
vom elektrostatischen Potential 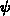 in der Poissongleichung
in der Poissongleichung
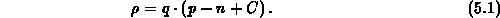
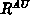 nach Auger (
nach Auger (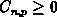 )
)

Die stationäre indirekte Rekombinationsrate
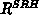 nach Shockley, Read und Hall
nach Shockley, Read und Hall
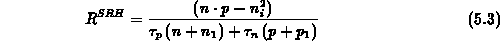
(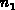 ,
,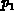 ,
,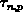
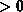 ) von den
Ladungsträgerkonzentrationen
) von den
Ladungsträgerkonzentrationen  und
und 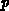 .
.




Die im Rahmen dieser Arbeit behandelten linearen Gleichungssysteme entstehen durch Diskretrisierung der linearisierten Halbleitergleichungen. Da zur Lösung des nichtlinearen, simultanen Gleichungssystems stets eine entkoppelte Iteration durchgeführt wird, brauchen nur die Einzelgleichungen diskretisiert werden. Verschiedene Quantitäten in den Halbleitergleichungen sind stark von den unabhängigen Variablen abhängig. Von diesen Abhängigkeiten werden bei der Linearisierung berücksichtigt:
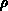 (siehe auch Gleichung (3.104))
vom elektrostatischen Potential
(siehe auch Gleichung (3.104))
vom elektrostatischen Potential 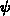 in der Poissongleichung
in der Poissongleichung
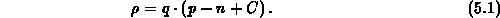
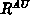 nach Auger (
nach Auger (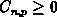 )
)

Die stationäre indirekte Rekombinationsrate
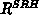 nach Shockley, Read und Hall
nach Shockley, Read und Hall
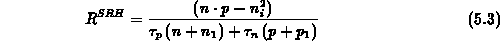
(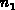 ,
,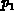 ,
,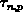
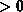 ) von den
Ladungsträgerkonzentrationen
) von den
Ladungsträgerkonzentrationen  und
und 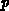 .
.
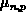 ,
in den Ladungsträgertemperaturen
(siehe Gleichung (5.12))
,
in den Ladungsträgertemperaturen
(siehe Gleichung (5.12))
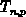 und in den
Stoßionisationsraten
und in den
Stoßionisationsraten 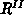 bleiben unberücksichtigt.
bleiben unberücksichtigt.
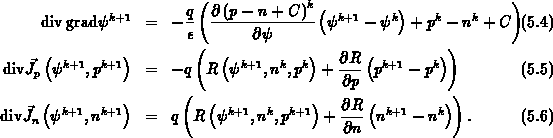
wobei 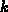 der Iterationszähler ist.
Die örtliche Diskretisierung der Kontinuitätsgleichungen
erfolgt unter Benützung
der exponentiellen Interpolationsformeln
(2.31)-(2.32) nach Scharfetter-Gummel,
wobei über finite Volumina integriert wird. Eine detaillierte
Beschreibung dieses Verfahren unter Berücksichtigung
nichtplanarer Grenzflächen findet man z.B. in [111].
der Iterationszähler ist.
Die örtliche Diskretisierung der Kontinuitätsgleichungen
erfolgt unter Benützung
der exponentiellen Interpolationsformeln
(2.31)-(2.32) nach Scharfetter-Gummel,
wobei über finite Volumina integriert wird. Eine detaillierte
Beschreibung dieses Verfahren unter Berücksichtigung
nichtplanarer Grenzflächen findet man z.B. in [111].
Besondere Aufmerksamkeit erfordert die Diskretisierung
der Kontinuitätsgleichungen für den verallgemeinerten
Drift-Diffusionsansatz der Stromdichten 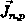 :
:
Die treibenden Kräfte 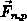 sind durch die Gleichungen
sind durch die Gleichungen
gegeben. Die Ladungsträgertemperaturen 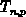 , die sich mit
den sogenannten elektronischen Spannungen
, die sich mit
den sogenannten elektronischen Spannungen 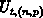 durch
die Gleichung
durch
die Gleichung
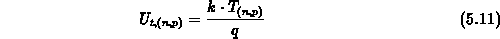
(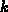 ist die Boltzmannkonstante)
verbinden lassen, können entweder aus einer Reihenentwicklung
der Energie-Erhaltungsgleichung
ist die Boltzmannkonstante)
verbinden lassen, können entweder aus einer Reihenentwicklung
der Energie-Erhaltungsgleichung [42]
[42]
oder direkt aus Monte-Carlo-Simulationen gewonnen werden [56].
Effekte der Geschwindigkeitssättigung
(Sättigungsgeschwindigkeit 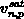 )
werden in der Formel
)
werden in der Formel
berücksichtigt. Der phänomenologische
Koeffizient 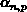 hat Defaultwerte
von
hat Defaultwerte
von 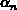 =
= für die Elektronen und
für die Elektronen und
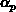 =
=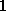 für die Löcher, die jedoch
den Bedürfnissen eines individuellen Beweglichkeitsmodells
angepaßt werden können.
für die Löcher, die jedoch
den Bedürfnissen eines individuellen Beweglichkeitsmodells
angepaßt werden können.
Zur Diskretisierung der beiden Kontinuitätsgleichungen
sind Mittenwertapproximationen für (5.7)
und (5.8) abzuleiten.
Unter der Annahme
einer linearen Variation von
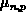 und
und 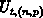 wird
zwischen benachbarten Gitterpunkten [
wird
zwischen benachbarten Gitterpunkten [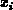 ,
, 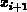 ]
eine lokale Kontinuitätsgleichung analytisch
gelöst. Man erhält daraus die Interpolationsformel
]
eine lokale Kontinuitätsgleichung analytisch
gelöst. Man erhält daraus die Interpolationsformel
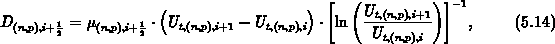
worin 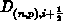 die Dimension
einer Diffusionskonstante besitzt.
Die Mittenapproximation der Ladungsträgerbeweglichkeiten,
die Dimension
einer Diffusionskonstante besitzt.
Die Mittenapproximation der Ladungsträgerbeweglichkeiten,
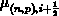 , entsteht durch lineare Interpolation.
Mit der Formel
, entsteht durch lineare Interpolation.
Mit der Formel
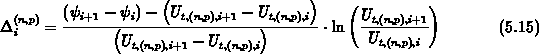
und der Bernoullifunktion 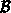
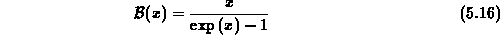
erhält man für den eindimensionalen diskreten Divergenzoperator die Differenzengleichungen
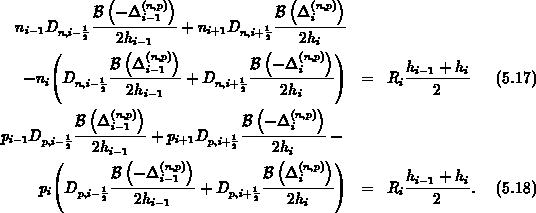
Im dreidimensionalen Fall erhält man sinngemäß eine
Koeffizientenmatrix mit sieben von Null verschiedenen Diagonalen.
Aufgrund des Tensor-Produkt-Gitters ist die Matrix zwei-zyklisch
(,,Eigenschaft A`` [114]).
Die Diagonaldominanz ergibt sich aus der
Tatsache, daß der Betrag des Hauptdiagonalelementes
gleich (oder bei positiven Beiträgen von Ableitungen
von 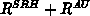 zur Hauptdiagonale größer)
der Spaltensumme der Nicht-Hauptdiagonalelemente ist.
Insbesondere ist die Koeffizientenmatrix werteunsymmetrisch.
zur Hauptdiagonale größer)
der Spaltensumme der Nicht-Hauptdiagonalelemente ist.
Insbesondere ist die Koeffizientenmatrix werteunsymmetrisch.
Im Fall räumlich konstanter
Ladungsträgertemperaturen 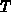 =
=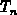 =
=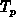 existieren
Matrizen
existieren
Matrizen 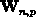 ,
mit denen die Koeffizientenmatrizen
,
mit denen die Koeffizientenmatrizen 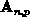 der
diskreten Kontinuitätsgleichungen durch
die Ähnlichkeitstransformation
der
diskreten Kontinuitätsgleichungen durch
die Ähnlichkeitstransformation
in symmetrisch positiv-definite Form gebracht werden können.
Die positiv-definiten Diagonalmatrizen 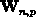 bestehen für Elektronen aus den Elementen
bestehen für Elektronen aus den Elementen
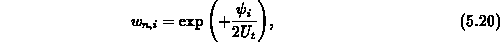
und für Löcher aus den Elementen
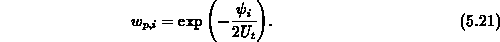
Diese Transformation ist das diskrete Pendant zur
Variablentransformation nach Slotboom [94].
Da durch eine Ähnlichkeitstransformation das Spektrum
einer Matrix nicht verändert wird, haben die
Koeffizientenmatrizen der diskreten Kontinuitätsgleichungen
(im klassischen Drift-Diffusionsmodell)
eine reelles, positives Spektrum. Für das
verallgemeinerte Drift-Diffusionsmodell kann eine solche
Beobachtung nicht gemacht werden.
Der benötigte Zahlenbereich der Elemente
der Transformationsmatrizen 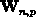 ist sehr
groß. Für ein elektrostatisches Potential von
ist sehr
groß. Für ein elektrostatisches Potential von 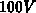 und eine Temperatur von
und eine Temperatur von 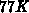 ist die Größe der
benötigten Exponenten
ist die Größe der
benötigten Exponenten 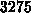 .
Mit vierfacher Zahlengenauigkeit ist dieser Bereich zu bewältigen.
Jedoch ist eine solche Zahlendarstellung in
FORTRAN nicht standardisiert, und nur wenige
Arithmetik-Prozessoren besitzen
die für solche Operationen
unbedingt benötigte Fließkomma-Hardware (FPU).
Die diskreten Halbleitergleichungen können deswegen in
einem praktischen, auf universeller Hardware einsetzbaren
Simulationsprogramm nicht
gemäß (5.19) symmetrisiert werden.
.
Mit vierfacher Zahlengenauigkeit ist dieser Bereich zu bewältigen.
Jedoch ist eine solche Zahlendarstellung in
FORTRAN nicht standardisiert, und nur wenige
Arithmetik-Prozessoren besitzen
die für solche Operationen
unbedingt benötigte Fließkomma-Hardware (FPU).
Die diskreten Halbleitergleichungen können deswegen in
einem praktischen, auf universeller Hardware einsetzbaren
Simulationsprogramm nicht
gemäß (5.19) symmetrisiert werden.



