Subsections

• 2.2.1 Basic Concepts

2.2 Finite Volumes

The finite volume method is the most natural discretization scheme, because it makes use of the conservation laws in integral form. It subdivides the domain into cells and evaluates the field equations in integral form on these cells. In the area of TCAD this method is often called the finite box method [26] to express the geometrical origin of the discretized domain. Most applications of the finite volume method do not include the time variable, which has to be enforced by a separate discretization. The concepts and implementation are simple for different dimensions and different types of cell complexes.

2.2.1 Basic Concepts

For the finite volume method the domain ${\ensuremath{\Omega}}$ is first subdivided into non-overlapping control volumes $V_i$ of a cell complex ${\ensuremath{\mathfrak{K}}}$ . In each control volume an integral conservation law is imposed [27]:

Definition 43 (Integral Conservation Law)   An integral conservation law asserts that the rate of change of the total amount of a quantity with density $u$ in a fixed control volume $V$ is equal to the total flux of the quantity through the boundary $\partial V$ .

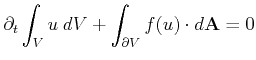$$\partial_t \int_{V} u  dV + \int_{\partial V} f(u) \cdot d\ensuremath{\mathbf{A}} = 0$$ (2.10)

By the step towards the discrete space, the integral conservation law is transfered to small control volumes:

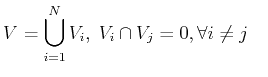$$V = \bigcup_{i=1}^{N} V_i, \; V_i \cap V_j = 0, \forall i \ne j \quad$$ (2.11)

Figure 2.4: Finite volume requirements for a primary and secondary cell complex.

The integral conservation law is readily obtained upon spatial integration of, e.g., a divergence equation in a region $\Omega_i$ . The choice of control volume tessellation is flexible in the finite volume method. The primary requirement is a secondary mesh (see Figure 2.4) with special properties related to the primary mesh.

Figure 2.5: Primary control volumes used in the finite volume method. Left: cell-centered. Right: vertex-centered.

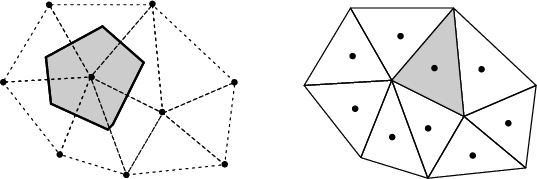In a vertex-centered method the control volumes are formed as a geometric dual to the cell complex and unknown solutions are stored on a per-vertex basis. In the cell-centered method the cells serve directly as control volumes containing the unknown solutions (degrees of freedom) stored on a per-cell basis. See Figure 2.5 for a graphical depiction of these two methods. The integral conservation law is enforced for each control volume and for the entire domain. To obtain a linear system of algebraic equations, integrals must be expressed in terms of mean values.

Two assumptions are fundamental to the finite volume method. First, a piecewise constant cell average is introduced for each control volume:

$$u_i = \frac{1}{\vert V_i\vert} \int_{V_i} u  dV$$ (2.12)

This cell average results in a discontinuity at the cell interfaces. The corresponding single solution flux is thereby ambiguous at the interface. A geometrical interpretation is given in Figure 2.6 for a one-dimensional cell complex.

Figure 2.6: Finite volume and the rendered cell average value within each cell for a one-dimensional cell complex.

Second, the true flux at the interfaces is replaced by a numerical flux function $g(u,v) : \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}$ . For arbitrary spatial dimensions, the flux integral is approximated by a numerical integration scheme, e.g., by a quadrature rule:

$$\int_{\partial V} f(u) \cdot d\ensuremath{\mathbf{A}} \approx \sum_{f_{jk} \in \partial V} g_{jk}(u_j,u_k)$$ (2.13)

The numerical flux has to satisfy the following properties:

• Flux conservation: the flux resulting from adjacent control volumes sharing an interface has to cancel exactly under summation:

  $$g_{j,k}(u,v) = -g_{kj}(v,u)$$ (2.14)

  
  

• Consistency: the numerical flux, evaluated with identical arguments, has to reduce to the true total flux passing through the boundary elements $f_{jk}$ :

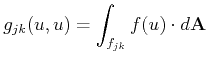  $$g_{jk}(u,u) = \int_{f_{jk}} f(u) \cdot d\ensuremath{\mathbf{A}}$$ (2.15)

  
  

Using Equation 2.12 and the previous interpretation of finite volumes for stationary meshes produces the following evolution equation for cell averages:

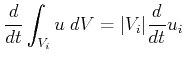$$\frac{d}{dt} \int_{V_i} u  dV = \vert V_i\vert \frac{d}{dt} u_i$$ (2.16)

One of the simplest finite volume schemes in a semi-discrete formulation can be obtained by utilizing representations which are continous in time, $t \in [0,\infty]$ , and piecewise constant in space, $u_h(t) \in V_h^0$ such that:

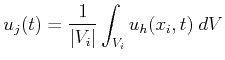$$u_j(t) = \frac{1}{\vert V_i\vert} \int_{V_i} u_h(x_i,t)  dV$$ (2.17)

with initial data

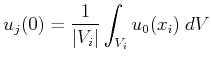$$u_j(0) = \frac{1}{\vert V_i\vert} \int_{V_i} u_0(x_i)  dV$$ (2.18)

and the numerical flux functions $g_{jk}(u_j,u_k)$ given by the following system of ordinary differential equations:

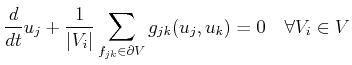$$\frac{d}{dt} u_j + \frac{1}{\vert V_i\vert} \sum_{f_{jk} \in \partial V} g_{jk}(u_j,u_k) = 0 \quad \forall V_i \in V$$ (2.19)

The final remaining issue is that the solution is available only at the computational nodes, the control volume centers. Interpolation is needed to obtain the function values at the vertices.

Using an explicit or implicit time integration formula [67], e.g., a forward Euler scheme:

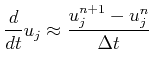$$\frac{d}{dt} u_j \approx \frac{u_j^{n+1} - u_j^n}{\Delta t}$$ (2.20)

produces a fully-discrete finite volume form:

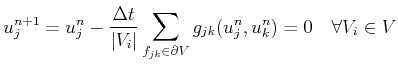$$u_j^{n+1} = u_j^n - \frac{\Delta t}{\vert V_i\vert} \sum_{f_{jk} \in \partial V} g_{jk}(u_j^n,u_k^n) = 0 \quad \forall V_i \in V$$ (2.21)