


Next: 4.3 Segregation Interface Condition
Up: 4. Oxidation of Doped
Previous: 4.1 Dopant Redistribution
Subsections
4.2 Five-Stream Dunham Diffusion Model
Dunham presented 1992 a general model [81] for the coupled diffusion of dopants with point defects, which includes the reaction of dopant-defect pairs with defects and other pairs, as well as all posible charge states for both dopants and pairs. It consists of five streams, because the comprehensive modeling of dopant behavior requires five differential equations, each treating a different concentration stream: one for the dopant atoms, two for the interstitial and vacancy point-defects, and two for the dopant-vacancy and dopant-interstitial pairs [24].
In silicon a dopant diffuses via interactions with point-defects, which can be described by a set of reactions. First, there are the dopant-defect pairing reactions
where 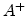 represent the ionized dopant atoms,
represent the ionized dopant atoms, 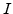 and
and 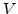 represent the interstitials and vacancies,
represent the interstitials and vacancies, 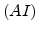 and
and 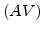 represent the dopant-defect pairs, and
represent the dopant-defect pairs, and 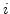 stands for the charge state of the defect or pair as
stands for the charge state of the defect or pair as 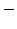 , 0,
, 0, 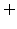 . Next, the recombination and generation of Frenkel pairs must be considered
. Next, the recombination and generation of Frenkel pairs must be considered
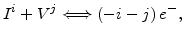 |
(4.4) |
where 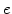 are electrons. A Frenkel pair is a vacancy-interstitial pair formed when an atom is displaced from a lattice site to an interstitial site.
are electrons. A Frenkel pair is a vacancy-interstitial pair formed when an atom is displaced from a lattice site to an interstitial site.
Additionally, the pairs can interact directly with the opposite type defect to produce a reaction which is equivalent to a pair dissociation followed by defect recombination
Finally, two opposite type pairs can recombine leaving two unpaired dopant atoms
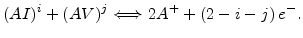 |
(4.7) |
The last three reactions provide an alternative path for the recombination and generation of vacancies and interstitials with the potential for a significant increase of the effective recombination rate for Frenkel pairs.
The five continuity equations for the total concentrations 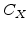 (X stands for A
(X stands for A , AI, AV, I, or V), over all charge states for a single donor species are [82]
, AI, AV, I, or V), over all charge states for a single donor species are [82]
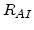 and
and 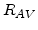 are the net rates of the dopant-defect pairing reactions (4.2) and (4.3) as defined in [81]:
are the net rates of the dopant-defect pairing reactions (4.2) and (4.3) as defined in [81]:
![$\displaystyle R_{AI}=\Big[\sum_i k_{AI}^i K_I^i \Big(\frac{n_i}{n}\Big)^i\Big]\Big[C_{A^+}C_{I^0}-\frac{C_{(AI)^+}}{K_{A+I}^0}\Big],$](img373.png) |
(4.13) |
![$\displaystyle R_{AV}=\Big[\sum_i k_{AV}^i K_V^i \Big(\frac{n_i}{n}\Big)^i\Big]\Big[C_{A^+}C_{V^0}-\frac{C_{(AV)^+}}{K_{A+V}^0}\Big].$](img374.png) |
(4.14) |
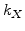 are the forward reaction rate coefficients and
are the forward reaction rate coefficients and 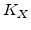 are the equilibrium constants.
are the equilibrium constants. 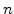 and
and 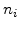 are the local and intrinsic carrier concentrations.
are the local and intrinsic carrier concentrations.
The net rate 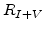 of Frenkel pair recombination (4.4) is [81]
of Frenkel pair recombination (4.4) is [81]
![$\displaystyle R_{AV}=\Big[\sum_{i,j} k_{I+V}^{i,j} K_I^i K_V^j \Big(\frac{n_i}{n}\Big)^{i+j}\Big]\big[C_{I^0}C_{V^0}-C_{I^0}^*C_{V^0}^*\big],$](img380.png) |
(4.15) |
where 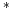 indicates equilibrium values.
indicates equilibrium values.
Finally, 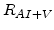 ,
, 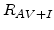 , and
, and 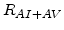 are the net rates of the pair-defect (4.5) (4.6) and pair-pair reactions (4.7) [81]:
are the net rates of the pair-defect (4.5) (4.6) and pair-pair reactions (4.7) [81]:
The continuity equations (4.30)-(4.30) also need the fluxes of mobile dopants, defects, and pairs. The total flux of interstitials is [81]
![$\displaystyle J_I=-\Big[\sum_{i} D_{I^i} K_{I}^i \Big(\frac{n_i}{n}\Big)^{i}\Big] \nabla C_{I^0},$](img388.png) |
(4.19) |
where 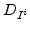 represents the diffusivity of interstitials of charge state
represents the diffusivity of interstitials of charge state 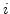 . Similarly, the total vacancy flux is [81]
. Similarly, the total vacancy flux is [81]
![$\displaystyle J_V=-\Big[\sum_{i} D_{V^i} K_{V}^i \Big(\frac{n_i}{n}\Big)^{i}\Big] \nabla C_{V^0}.$](img390.png) |
(4.20) |
The total pair fluxes are [81]
![$\displaystyle J_{AI}=-\Big[\sum_{i} D_{AI^{i+1}} K_{AI}^i \Big(\frac{n_i}{n}\Bi...
...)^+}+ C_{(AI)^+} \Big(\frac{n_i}{n}\Big) \nabla \Big(\frac{n}{n_i}\Big) \Big],$](img391.png) |
(4.21) |
![$\displaystyle J_{AV}=-\Big[\sum_{i} D_{AV^{i+1}} K_{AV}^i \Big(\frac{n_i}{n}\Bi...
...^+}+ C_{(AV)^+} \Big(\frac{n_i}{n}\Big) \nabla \Big(\frac{n}{n_i} \Big) \Big],$](img392.png) |
(4.22) |
where 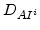 and
and 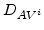 are the diffusivities of dopant-defect pairs with charge
are the diffusivities of dopant-defect pairs with charge 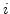 .
.



Next: 4.3 Segregation Interface Condition
Up: 4. Oxidation of Doped
Previous: 4.1 Dopant Redistribution
Ch. Hollauer: Modeling of Thermal Oxidation and Stress Effects
![$\displaystyle R_{AI}=\Big[\sum_i k_{AI}^i K_I^i \Big(\frac{n_i}{n}\Big)^i\Big]\Big[C_{A^+}C_{I^0}-\frac{C_{(AI)^+}}{K_{A+I}^0}\Big],$](img373.png)
![$\displaystyle R_{AV}=\Big[\sum_i k_{AV}^i K_V^i \Big(\frac{n_i}{n}\Big)^i\Big]\Big[C_{A^+}C_{V^0}-\frac{C_{(AV)^+}}{K_{A+V}^0}\Big].$](img374.png)
![]() of Frenkel pair recombination (4.4) is [81]
of Frenkel pair recombination (4.4) is [81]
![$\displaystyle R_{AV}=\Big[\sum_{i,j} k_{I+V}^{i,j} K_I^i K_V^j \Big(\frac{n_i}{n}\Big)^{i+j}\Big]\big[C_{I^0}C_{V^0}-C_{I^0}^*C_{V^0}^*\big],$](img380.png)
![]() ,
, ![]() , and
, and ![]() are the net rates of the pair-defect (4.5) (4.6) and pair-pair reactions (4.7) [81]:
are the net rates of the pair-defect (4.5) (4.6) and pair-pair reactions (4.7) [81]:
![$\displaystyle R_{AI+V}=\Big[\sum_{i,j} k_{AI+V}^{i,j} K_{AI}^i K_V^j \Big(\frac...
...)^{i+j}\Big]\big[C_{(AI)^+}C_{V^0}- K_{A+I}^0 C_{I^0}^* C_{V^0}^*C_{A^+} \big],$](img385.png)
![$\displaystyle R_{AV+I}=\Big[\sum_{i,j} k_{AV+I}^{i,j} K_{AV}^i K_I^j \Big(\frac...
...)^{i+j}\Big]\big[C_{(AV)^+}C_{I^0}- K_{A+V}^0 C_{I^0}^* C_{V^0}^*C_{A^+} \big],$](img386.png)
![$\displaystyle R_{AI+AV}=\Big[\sum_{i,j} k_{AI+AV}^{i,j} K_{AI}^i K_{AV}^j \Big(...
...C_{(AI)^+}C_{(AV)^+}- K_{A+I}^0 K_{A+V}^0 C_{I^0}^* C_{V^0}^*(C_{A^+})^2 \big].$](img387.png)
![$\displaystyle J_I=-\Big[\sum_{i} D_{I^i} K_{I}^i \Big(\frac{n_i}{n}\Big)^{i}\Big] \nabla C_{I^0},$](img388.png)
![$\displaystyle J_V=-\Big[\sum_{i} D_{V^i} K_{V}^i \Big(\frac{n_i}{n}\Big)^{i}\Big] \nabla C_{V^0}.$](img390.png)
![$\displaystyle J_{AI}=-\Big[\sum_{i} D_{AI^{i+1}} K_{AI}^i \Big(\frac{n_i}{n}\Bi...
...)^+}+ C_{(AI)^+} \Big(\frac{n_i}{n}\Big) \nabla \Big(\frac{n}{n_i}\Big) \Big],$](img391.png)
![$\displaystyle J_{AV}=-\Big[\sum_{i} D_{AV^{i+1}} K_{AV}^i \Big(\frac{n_i}{n}\Bi...
...^+}+ C_{(AV)^+} \Big(\frac{n_i}{n}\Big) \nabla \Big(\frac{n}{n_i} \Big) \Big],$](img392.png)