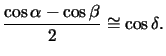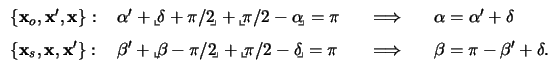Next: B. Analytical Fourier Transformations
Up: PhD Thesis Heinrich Kirchauer
Previous: Physical modeling.
A. Approximation of the Inclination Factor
During the derivation of the Fresnel and the Fraunhofer diffraction
formulae (4.14) and (4.15), respectively,
the inclination factor occurring in (4.10) has been
approximated under the assumption that the source
xs as well as the
observation point
xo are located near the optical axis
(cf. Figure 4.1).
We will now explain how this approximation is obtained.
First we define three angles 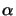 ,
, 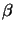 , and
, and 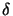 guided by Figure 4.1 and shown in
Figure A.1:
guided by Figure 4.1 and shown in
Figure A.1:
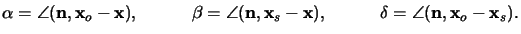 |
(A.1) |
The approximation of the inclination
factor--compare (4.12)
with (4.14) or (4.15)--thus writes to
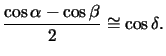 |
(A.2) |
Furthermore we introduce the two auxiliary angles
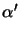 and
and
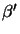 as illustrated in Figure A.1.
In the situation of interest the two points
xs and
xo are
near the optical axis and thus
as illustrated in Figure A.1.
In the situation of interest the two points
xs and
xo are
near the optical axis and thus
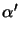 ,
,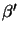
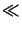 1
yielding
1
yielding
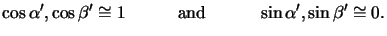 |
(A.3) |
By noting that the sum of the angles of the two triangles
{xo,x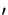 ,x} and
{xs,x,x
,x} and
{xs,x,x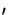 } equals
} equals 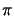 ,
we geta
,
we geta
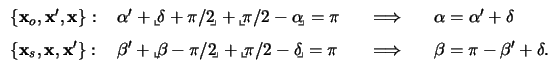 |
(A.4) |
With these two expressions for 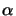 and
and 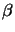 and the approximations
listed in (A.3), the derivation of (A.2)
is straight forward:
and the approximations
listed in (A.3), the derivation of (A.2)
is straight forward:
Figure A.1:
Approximation of
the inclination factor. The dashed lines indicate the two
auxiliary triangles used throughout the derivation.
|
|
Footnotes
- ... geta
- The terms
forming one common triangle-angle are indicated by delimiters
(cf. Figure A.1).




Next: B. Analytical Fourier Transformations
Up: PhD Thesis Heinrich Kirchauer
Previous: Physical modeling.
Heinrich Kirchauer, Institute for Microelectronics, TU Vienna
1998-04-17
![]() ,
, ![]() , and
, and ![]() guided by Figure 4.1 and shown in
Figure A.1:
guided by Figure 4.1 and shown in
Figure A.1: